Article contents
Reflection of a rightward-moving oblique shock of first family over a steady oblique shock wave
Published online by Cambridge University Press: 12 January 2024
Abstract
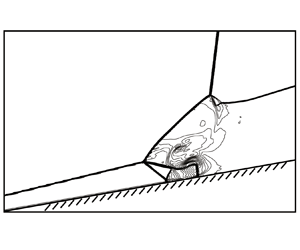
The reflection of a rightward-moving oblique shock (RMOS) belonging to the first family, over an initially steady oblique shock wave (SOSW) produced by a wedge, is studied in this paper. To cover all possibilities, the problem is divided into a pre-shock reflection problem, for which the incident shock is assumed to reflect over the pre-interaction part of the SOSW, and a post-shock reflection problem, for which the incident shock is assumed to reflect over the post-interaction part. Such division, together with the definition of the equivalent problem defined on the reference frame co-moving with the nominal intersection point of the two shock waves, allows us to connect the reflection patterns with the six types of shock interference of Edney, which include type I–VI shock interferences depending on how an upstream oblique shock intersects a bow shock (types I and II are regular and Mach reflections of two shocks from the opposite sides; type III and type IV have two triple points or two Mach reflection configuration; type V and type VI are irregular and regular reflections of two shocks from the same side). We are thus able to identify all possible shock reflection types and find their transition conditions. Pre-shock reflection may yield IV, V and VI (of Edney's six types) shock interferences and post-shock reflection may yield I, II and III shock interferences. Pre- and post-shock reflections possibly occur at two different parts of the SOSW, and the complete reflection configuration may have one or both of them. Both transition condition study and numerical simulation are used to show how pre-shock reflection and post-shock reflection exist alone or coexist, leading to various types of combined pre-shock and post-shock reflections.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 1
- Cited by



