Published online by Cambridge University Press: 18 October 2019
Many aquatic animals propel themselves by generating backward traveling waves over their body, which is thought to reattach the flow when the wave speed ( $C=\unicode[STIX]{x1D706}f$, where
$C=\unicode[STIX]{x1D706}f$, where 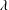 $\unicode[STIX]{x1D706}$ is wavelength and
$\unicode[STIX]{x1D706}$ is wavelength and 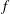 $f$ is frequency) is larger than the swimming speed (
$f$ is frequency) is larger than the swimming speed (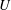 $U$). This has inspired the use of travelling waves, which have recently been generated at low amplitudes using smart materials, to reduce flow separation on an inclined plate. To see if low-amplitude travelling waves (amplitude approximately 0.01 of chord length
$U$). This has inspired the use of travelling waves, which have recently been generated at low amplitudes using smart materials, to reduce flow separation on an inclined plate. To see if low-amplitude travelling waves (amplitude approximately 0.01 of chord length 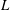 $L$) can reduce the separation on an inclined plate, large-eddy simulations are performed. The simulations are carried out for Reynolds number (
$L$) can reduce the separation on an inclined plate, large-eddy simulations are performed. The simulations are carried out for Reynolds number (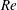 $Re$) 20 000 and an angle of attack of
$Re$) 20 000 and an angle of attack of 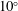 $10^{\circ }$ with different wavelengths and frequencies. The travelling waves at a low reduced frequency (
$10^{\circ }$ with different wavelengths and frequencies. The travelling waves at a low reduced frequency (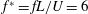 $f^{\ast }=fL/U=6$ and
$f^{\ast }=fL/U=6$ and 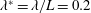 $\unicode[STIX]{x1D706}^{\ast }=\unicode[STIX]{x1D706}/L=0.2$, where
$\unicode[STIX]{x1D706}^{\ast }=\unicode[STIX]{x1D706}/L=0.2$, where 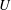 $U$ is free-stream velocity) do not affect the flow separation and aerodynamic performance compared to the flat inclined plate. Nevertheless, increasing the wave speed by increasing the reduced frequency to 20 and 30 reduces flow separation. However, increasing the wave speed by increasing the wavelength, in contrast to the common belief, does not monotonically reduce the flow separation. In fact, increasing the wave speed by increasing the wavelength from 0.15 to 0.5 at constant frequency
$U$ is free-stream velocity) do not affect the flow separation and aerodynamic performance compared to the flat inclined plate. Nevertheless, increasing the wave speed by increasing the reduced frequency to 20 and 30 reduces flow separation. However, increasing the wave speed by increasing the wavelength, in contrast to the common belief, does not monotonically reduce the flow separation. In fact, increasing the wave speed by increasing the wavelength from 0.15 to 0.5 at constant frequency 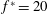 $f^{\ast }=20$ increases the separation, but increasing from 0.5 to 1.0 and 2.0, interestingly, reduces flow separation. These observations indicate that the wave speed is not the only parameter for flow reattachment, but both wavelength and frequency individually impact flow separation by affecting two competing but interconnected mechanisms: the axial momentum, imparted onto the fluid by the undulations, tends to reattach the flow but the lateral velocity tends to detach it. In fact, increasing
$f^{\ast }=20$ increases the separation, but increasing from 0.5 to 1.0 and 2.0, interestingly, reduces flow separation. These observations indicate that the wave speed is not the only parameter for flow reattachment, but both wavelength and frequency individually impact flow separation by affecting two competing but interconnected mechanisms: the axial momentum, imparted onto the fluid by the undulations, tends to reattach the flow but the lateral velocity tends to detach it. In fact, increasing 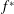 $f^{\ast }$ and
$f^{\ast }$ and 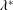 $\unicode[STIX]{x1D706}^{\ast }$ increases both the axial momentum and the lateral velocity, which are competing to attach and detach the flow, respectively.
$\unicode[STIX]{x1D706}^{\ast }$ increases both the axial momentum and the lateral velocity, which are competing to attach and detach the flow, respectively.