Article contents
Reduced-order analysis of buffet flow of space launchers
Published online by Cambridge University Press: 14 February 2017
Abstract
A reduced-order analysis based on optimized dynamic mode decomposition (DMD) is performed on the turbulent wake of a generic axisymmetric space launcher configuration computed via a zonal large-eddy simulation at the free stream Mach number 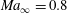 $Ma_{\infty }=0.8$ and the Reynolds number based on the main body diameter
$Ma_{\infty }=0.8$ and the Reynolds number based on the main body diameter 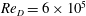 $Re_{D}=6\times 10^{5}$ to investigate the buffet phenomenon. The transonic wake is characterized by an unsteady recirculation region occurring around the nozzle due to the separation of the turbulent boundary layer at the main body shoulder and subsequent dynamic interaction of the unstable free-shear layer with the nozzle surface. This results in strongly periodic and antisymmetric wall pressure fluctuations, for which three distinct frequency ranges are identified using conventional spectral analysis, i.e.
$Re_{D}=6\times 10^{5}$ to investigate the buffet phenomenon. The transonic wake is characterized by an unsteady recirculation region occurring around the nozzle due to the separation of the turbulent boundary layer at the main body shoulder and subsequent dynamic interaction of the unstable free-shear layer with the nozzle surface. This results in strongly periodic and antisymmetric wall pressure fluctuations, for which three distinct frequency ranges are identified using conventional spectral analysis, i.e. 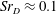 $Sr_{D}\approx 0.1$,
$Sr_{D}\approx 0.1$, 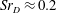 $Sr_{D}\approx 0.2$ and
$Sr_{D}\approx 0.2$ and 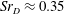 $Sr_{D}\approx 0.35$. For the spatially integrated side (buffet) loads on the nozzle, the second range is found to be energetically most dominant. To clarify the origin of the detected wake dynamics, the underlying spatio-temporal coherent modes are extracted using DMD. Subsequent analysis of the reduced-order modelled flow field based on the identified DMD modes reveals that at
$Sr_{D}\approx 0.35$. For the spatially integrated side (buffet) loads on the nozzle, the second range is found to be energetically most dominant. To clarify the origin of the detected wake dynamics, the underlying spatio-temporal coherent modes are extracted using DMD. Subsequent analysis of the reduced-order modelled flow field based on the identified DMD modes reveals that at 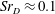 $Sr_{D}\approx 0.1$ a longitudinal cross-pumping motion of the separation bubble takes place, caused by a harmonic antisymmetric oscillation of the main recirculation vortex in the streamwise direction. At
$Sr_{D}\approx 0.1$ a longitudinal cross-pumping motion of the separation bubble takes place, caused by a harmonic antisymmetric oscillation of the main recirculation vortex in the streamwise direction. At 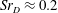 $Sr_{D}\approx 0.2$, a cross-flapping motion of the shear layer is determined, triggered by antisymmetric vortex shedding which is in phase with the cross-pumping motion such that it occurs at twice the frequency value. The last range of
$Sr_{D}\approx 0.2$, a cross-flapping motion of the shear layer is determined, triggered by antisymmetric vortex shedding which is in phase with the cross-pumping motion such that it occurs at twice the frequency value. The last range of 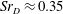 $Sr_{D}\approx 0.35$ is attributed to a swinging motion of the shear layer caused by a higher harmonic of the vortex shedding mode. Conclusively, the controversial aspect of the true three-dimensional shape of the antisymmetric mode at
$Sr_{D}\approx 0.35$ is attributed to a swinging motion of the shear layer caused by a higher harmonic of the vortex shedding mode. Conclusively, the controversial aspect of the true three-dimensional shape of the antisymmetric mode at 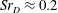 $Sr_{D}\approx 0.2$ that dominates the buffet phenomenon is scrutinized. Inclined elongated closed-loop vortices are identified that are shed in alternating sequence from azimuthally opposite positions in a longitudinal plane of symmetry that changes its momentary orientation irregularly, maintaining an axisymmetric time-averaged field and spatially isotropic buffet loads.
$Sr_{D}\approx 0.2$ that dominates the buffet phenomenon is scrutinized. Inclined elongated closed-loop vortices are identified that are shed in alternating sequence from azimuthally opposite positions in a longitudinal plane of symmetry that changes its momentary orientation irregularly, maintaining an axisymmetric time-averaged field and spatially isotropic buffet loads.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
Statnikov et al. supplementary movie
Reduced-order modeled streamwise velocity field for the characteristic frequency SrD(λ1) ≈ 0.1
Statnikov et al. supplementary movie
Reduced-order modeled streamwise velocity field for the characteristic frequency SrD(λ2) ≈ 0.2
Statnikov et al. supplementary movie
Reduced-order modeled streamwise velocity field for the characteristic frequency SrD(λ3) ≈ 0.35
Statnikov et al. supplementary movie
Streamline plots of the reduced-order modeled composite velocity field for the characteristic frequency SrD(λ1) ≈ 0.1
Statnikov et al. supplementary movie
Streamline plots of the reduced-order modeled composite velocity field for the characteristic frequency SrD(λ2) ≈ 0.2
Statnikov et al. supplementary movie
Streamline plots of the reduced-order modeled composite velocity field for the characteristic frequency SrD(λ3) ≈ 0.35
Statnikov et al. supplementary movie
Reduced-order modeled pressure field for the characteristic frequency SrD(λ1) ≈ 0.1
Statnikov et al. supplementary movie
Reduced-order modeled pressure field for the characteristic frequency SrD(λ2) ≈ 0.2
Statnikov et al. supplementary movie
Reduced-order modeled pressure field for the characteristic frequency SrD(λ3) ≈ 0.35
Statnikov et al. supplementary movie
Visualization of the three-dimensional shape of the antisymmetric modes at SrD ≈ 0.2 using pressure iso-surface in side and top view, i.e., x − z and x − y planes, color-coded by the streamwise coordinate x/D. The nozzle wall is color-coded by the pressure coefficient increment cp′
- 43
- Cited by



