Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-30T22:53:54.389Z Has data issue: false hasContentIssue false
  • English
  • Français

Reduced particle settling speed in turbulence

Published online by Cambridge University Press:  27 October 2016

Walter Fornari ,
Francesco Picano ,
Gaetano Sardina  and
Luca Brandt
Walter Fornari*
Affiliation:
Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, SE-100 44 Stockholm, Sweden
Francesco Picano
Affiliation:
Department of Industrial Engineering, University of Padova, Via Venezia 1, 35131 Padua, Italy
Gaetano Sardina
Affiliation:
Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, SE-100 44 Stockholm, Sweden
Luca Brandt
Affiliation:
Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

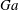We study the settling of finite-size rigid spheres in sustained homogeneous isotropic turbulence (HIT) by direct numerical simulations using an immersed boundary method to account for the dispersed solid phase. We study semi-dilute suspensions at different Galileo numbers, $Ga$. The Galileo number is the ratio between buoyancy and viscous forces, and is here varied via the solid-to-fluid density ratio 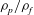$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$. The focus is on particles that are slightly heavier than the fluid. We find that in HIT, the mean settling speed is less than that in quiescent fluid; in particular, it reduces by 6 %–60 % with respect to the terminal velocity of an isolated sphere in quiescent fluid as the ratio between the latter and the turbulent velocity fluctuations 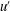$u^{\prime }$ is decreased. Analysing the fluid–particle relative motion, we find that the mean settling speed is progressively reduced while reducing 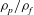$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$ due to the increase of the vertical drag induced by the particle cross-flow velocity. Unsteady effects contribute to the mean overall drag by about 6 %–10 %. The probability density functions of particle velocities and accelerations reveal that these are closely related to the features of the turbulent flow. The particle mean-square displacement in the settling direction is found to be similar for all 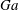$Ga$ if time is scaled by 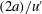$(2a)/u^{\prime }$ (where 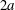$2a$ is the particle diameter and 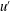$u^{\prime }$ is the turbulence velocity root mean square).

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 808 , 10 December 2016 , pp. 153 - 167
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.CrossRefGoogle Scholar
Bagchi, P. & Balachandar, S. 2003 Effect of turbulence on the drag and lift of a particle. Phys. Fluids 15 (11), 3496–3513.CrossRefGoogle Scholar
Bellani, G. & Variano, E. A. 2012 Slip velocity of large neutrally buoyant particles in turbulent flows. New J. Phys. 14 (12), 125009.CrossRefGoogle Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16 (3), 242–251.CrossRefGoogle Scholar
Breugem, W.-P. 2012 A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. J. Comput. Phys. 231 (13), 4469–4498.CrossRefGoogle Scholar
Byron, M. L.2015 The rotation and translation of non-spherical particles in homogeneous isotropic turbulence. PhD thesis, Department of Civil and Environmental Engineering, University of California Berkeley.Google Scholar
Chang, E. J. & Maxey, M. R. 1995 Unsteady flow about a sphere at low to moderate Reynolds number. Part 2. Accelerated motion. J. Fluid Mech. 303, 133–153.CrossRefGoogle Scholar
Chouippe, A. & Uhlmann, M. 2015 Forcing homogeneous turbulence in direct numerical simulation of particulate flow with interface resolution and gravity. Phys. Fluids 27 (12), 123301.CrossRefGoogle Scholar
Cisse, M., Homann, H. & Bec, J. 2013 Slipping motion of large neutrally buoyant particles in turbulence. J. Fluid Mech. 735, R1.CrossRefGoogle Scholar
Di Felice, R. 1999 The sedimentation velocity of dilute suspensions of nearly monosized spheres. Intl J. Multiphase Flow 25 (4), 559–574.CrossRefGoogle Scholar
Fornari, W., Formenti, A., Picano, F. & Brandt, L. 2016a The effect of particle density in turbulent channel flow laden with finite size particles in semi-dilute conditions. Phys. Fluids 28 (3), 033301.CrossRefGoogle Scholar
Fornari, W., Picano, F. & Brandt, L. 2016b Sedimentation of finite-size spheres in quiescent and turbulent environments. J. Fluid Mech. 788, 640–669.CrossRefGoogle Scholar
Good, G. H., Ireland, P. J., Bewley, G. P., Bodenschatz, E., Collins, L. R. & Warhaft, Z. 2014 Settling regimes of inertial particles in isotropic turbulence. J. Fluid Mech. 759, R3.CrossRefGoogle Scholar
Guazzelli, E. & Morris, J. F. 2011 A Physical Introduction to Suspension Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Homann, H. & Bec, J. 2010 Finite-size effects in the dynamics of neutrally buoyant particles in turbulent flow. J. Fluid Mech. 651, 81–91.CrossRefGoogle Scholar
Homann, H., Bec, J. & Grauer, R. 2013 Effect of turbulent fluctuations on the drag and lift forces on a towed sphere and its boundary layer. J. Fluid Mech. 721, 155–179.CrossRefGoogle Scholar
Kawanisi, K. & Shiozaki, R. 2008 Turbulent effects on the settling velocity of suspended sediment. ASCE J. Hydraul. Engng 134 (2), 261–266.CrossRefGoogle Scholar
Kidanemariam, A. G., Chan-Braun, C., Doychev, T. & Uhlmann, M. 2013 Direct numerical simulation of horizontal open channel flow with finite-size, heavy particles at low solid volume fraction. New J. Phys. 15 (2), 025031.CrossRefGoogle Scholar
Lambert, R. A., Picano, F., Breugem, W.-P. & Brandt, L. 2013 Active suspensions in thin films: nutrient uptake and swimmer motion. J. Fluid Mech. 733, 528–557.CrossRefGoogle Scholar
Lashgari, I., Picano, F., Breugem, W. P. & Brandt, L. 2016 Channel flow of rigid sphere suspensions: particle dynamics in the inertial regime. Intl J. Multiphase Flow 78, 12–24.CrossRefGoogle Scholar
Mathai, V., Prakash, V. N., Brons, J., Sun, C. & Lohse, D. 2015 Wake-driven dynamics of finite-sized buoyant spheres in turbulence. Phys. Rev. Lett. 115 (12), 124501.CrossRefGoogle ScholarPubMed
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.CrossRefGoogle Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.CrossRefGoogle Scholar
Merle, A., Legendre, D. & Magnaudet, J. 2005 Forces on a high-Reynolds-number spherical bubble in a turbulent flow. J. Fluid Mech. 532, 53–62.CrossRefGoogle Scholar
Murray, S. P. 1970 Settling velocities and vertical diffusion of particles in turbulent water. J. Geophys. Res. 75 (9), 1647–1654.CrossRefGoogle Scholar
Nielsen, P. 1993 Turbulence effects on the settling of suspended particles. J. Sedim. Res. 63 (5), 835–838.Google Scholar
Olivieri, S., Picano, F., Sardina, G., Iudicone, D. & Brandt, L. 2014 The effect of the basset history force on particle clustering in homogeneous and isotropic turbulence. Phys. Fluids 26 (4), 041704.CrossRefGoogle Scholar
Picano, F., Breugem, W.-P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.CrossRefGoogle Scholar
Schiller, L. & Naumann, A. 1935 A drag coefficient correlation. Vdi Zeitung 77 (318), 51.Google Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3 (5), 1169–1178.CrossRefGoogle Scholar
Uhlmann, M. & Doychev, T. 2014 Sedimentation of a dilute suspension of rigid spheres at intermediate Galileo numbers: the effect of clustering upon the particle motion. J. Fluid Mech. 752, 310–348.CrossRefGoogle Scholar
Vincent, A. & Meneguzzi, M. 1991 The satial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.CrossRefGoogle Scholar
Wang, L.-P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.CrossRefGoogle Scholar
Yang, T. S. & Shy, S. S. 2003 The settling velocity of heavy particles in an aqueous near-isotropic turbulence. Phys. Fluids 15 (4), 868–880.CrossRefGoogle Scholar
Yang, T. S. & Shy, S. S. 2005 Two-way interaction between solid particles and homogeneous air turbulence: particle settling rate and turbulence modification measurements. J. Fluid Mech. 526, 171–216.CrossRefGoogle Scholar
Yin, X. & Koch, D. L. 2007 Hindered settling velocity and microstructure in suspensions of solid spheres with moderate Reynolds numbers. Phys. Fluids 19 (9), 093302.CrossRefGoogle Scholar
Zaidi, A. A., Tsuji, T. & Tanaka, T. 2014 Direct numerical simulation of finite sized particles settling for high Reynolds number and dilute suspension. Intl J. Heat Fluid Flow 50, 330–341.CrossRefGoogle Scholar