Hostname: page-component-f554764f5-nqxm9 Total loading time: 0 Render date: 2025-04-23T01:41:39.109Z Has data issue: false hasContentIssue false
  • English
  • Français

A reciprocal theorem for biphasic poro-viscoelastic materials

Published online by Cambridge University Press:  17 October 2024

Moslem Moradi Open the ORCID record for Moslem Moradi [Opens in a new window] ,
Wenzheng Shi Open the ORCID record for Wenzheng Shi [Opens in a new window]  and
Ehssan Nazockdast Open the ORCID record for Ehssan Nazockdast [Opens in a new window]
Moslem Moradi
Affiliation:
Department of Applied Physical Sciences, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599-3250, USA Department of Chemical Engineering, University of Pittsburgh, Pittsburgh, PA 15261, USA
Wenzheng Shi
Affiliation:
Department of Applied Physical Sciences, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599-3250, USA
Ehssan Nazockdast*
Affiliation:
Department of Applied Physical Sciences, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599-3250, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

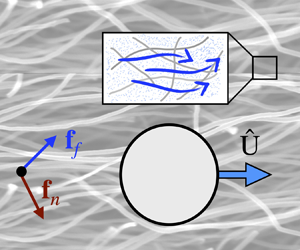
In studying the transport of inclusions in multiphase systems we are often interested in integrated quantities such as the net force and the net velocity of the inclusions. In the reciprocal theorem the known solution to the first and typically easier boundary value problem is used to compute the integrated quantities, such as the net force, in the second problem without the need to solve that problem. Here, we derive a reciprocal theorem for poro-viscoelastic (or biphasic) materials that are composed of a linear compressible solid phase, permeated by a viscous fluid. As an example, we analytically calculate the time-dependent net force on a rigid sphere in response to point forces applied to the elastic network and the Newtonian fluid phases of the biphasic material. We show that when the point force is applied to the fluid phase, the net force on the sphere evolves over time scales that are independent of the distance between the point force and the sphere; in comparison, when the point force is applied to the elastic phase, the time scale for force development increases quadratically with the distance, in line with the scaling of poroelastic relaxation time. Finally, we formulate and discuss how the reciprocal theorem can be applied to other areas, including (i) calculating the network slip on the sphere's surface, (ii) computing the leading-order effects of nonlinearities in the fluid and network forces and stresses, and (iii) calculating self-propulsion in biphasic systems.

JFM classification

Low-Reynolds-number flows: Boundary integral methods Low-Reynolds-number flows: Porous media Low-Reynolds-number flows: Stokesian dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 997 , 25 October 2024 , A62
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abate, J. & Whitt, W. 1992 The Fourier-series method for inverting transforms of probability distributions. Queueing Syst. 10 (1), 5–87.CrossRefGoogle Scholar
Arfken, G.B. & Weber, H.J. 1999 Mathematical Methods for Physicists. American Association of Physics Teachers.Google Scholar
Auriault, J.-L. 2009 On the domain of validity of Brinkman's equation. Transp. Porous Media 79 (2), 215–223.CrossRefGoogle Scholar
Becker, L.E., Koehler, S.A. & Stone, H.A. 2003 On self-propulsion of micro-machines at low Reynolds number: Purcell's three-link swimmer. J. Fluid Mech. 490, 15–35.CrossRefGoogle Scholar
Biot, M.A. 1941 General theory of three-dimensional consolidation. J. Appl. Phys. 12 (2), 155–164.CrossRefGoogle Scholar
Biot, M.A. 1955 Theory of elasticity and consolidation for a porous anisotropic solid. J. Appl. Phys. 26 (2), 182–185.CrossRefGoogle Scholar
Boyko, E. & Stone, H.A. 2021 Reciprocal theorem for calculating the flow rate–pressure drop relation for complex fluids in narrow geometries. Phys. Rev. Fluids 6 (8), L081301.CrossRefGoogle Scholar
Brady, J.F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.CrossRefGoogle Scholar
Burla, F., Mulla, Y., Vos, B.E., Aufderhorst-Roberts, A. & Koenderink, G.H. 2019 From mechanical resilience to active material properties in biopolymer networks. Nat. Rev. Phys. 1 (4), 249–263.CrossRefGoogle Scholar
Camley, B.A. & Rappel, W.-J. 2017 Physical models of collective cell motility: from cell to tissue. J. Phys. D: Appl. Phys. 50 (11), 113002.CrossRefGoogle Scholar
Carrillo, F.J. & Bourg, I.C. 2019 A Darcy-Brinkman-Biot approach to modeling the hydrology and mechanics of porous media containing macropores and deformable microporous regions. Water Resour. Res. 55 (10), 8096–8121.CrossRefGoogle Scholar
Carrillo, F.J., Bourg, I.C. & Soulaine, C. 2020 Multiphase flow modeling in multiscale porous media: an open-source micro-continuum approach. J. Comput. Phys. X 8, 100073.Google Scholar
Charras, G.T., Coughlin, M., Mitchison, T.J. & Mahadevan, L. 2008 Life and times of a cellular bleb. Biophys. J. 94 (5), 1836–1853.CrossRefGoogle Scholar
Charras, G.T., Yarrow, J.C., Horton, M.A., Mahadevan, L. & Mitchison, T.J. 2005 Non-equilibration of hydrostatic pressure in blebbing cells. Nature 435 (7040), 365–369.CrossRefGoogle Scholar
Cheng, A.H.-D. 2016 Poroelasticity, vol. 27. Springer.CrossRefGoogle Scholar
Cheng, A.H.-D. & Predeleanu, M. 1987 Transient boundary element formulation for linear poroelasticity. Appl. Math. Model. 11 (4), 285–290.CrossRefGoogle Scholar
Cowin, S.C. & Doty, S.B. 2007 Tissue Mechanics. Springer.CrossRefGoogle Scholar
Cremer, T., Cremer, M., Hübner, B., Silahtaroglu, A., Hendzel, M., Lanctôt, C., Strickfaden, H. & Cremer, C. 2020 The interchromatin compartment participates in the structural and functional organization of the cell nucleus. BioEssays 42 (2), 1900132.CrossRefGoogle Scholar
Detournay, E. & Cheng, A.H.-D. 1993 Fundamentals of poroelasticity. In Analysis and Design Methods, pp. 113–171. Elsevier.CrossRefGoogle Scholar
Doi, M. 2009 Gel dynamics. J. Phys. Soc. Japan 78 (5), 052001.CrossRefGoogle Scholar
Dumais, J. & Forterre, Y. 2012 ‘Vegetable dynamicks’: the role of water in plant movements. Annu. Rev. Fluid Mech. 44, 453–478.CrossRefGoogle Scholar
Elfring, G.J. 2015 A note on the reciprocal theorem for the swimming of simple bodies. Phys. Fluids 27 (2), 023101.CrossRefGoogle Scholar
Elfring, G.J. & Lauga, E. 2015 Theory of locomotion through complex fluids. In Complex Fluids in Biological Systems: Experiment, Theory, and Computation, pp. 283–317. Springer.CrossRefGoogle Scholar
Elfring, G.J., Leal, L.G. & Squires, T.M. 2016 Surface viscosity and marangoni stresses at surfactant laden interfaces. J. Fluid Mech. 792, 712–739.CrossRefGoogle Scholar
Esteki, M.H., Malandrino, A., Alemrajabi, A.A., Sheridan, G.K., Charras, G. & Moeendarbary, E. 2021 Poroelastic osmoregulation of living cell volume. Iscience 24 (12), 103482.CrossRefGoogle Scholar
Fiore, A.M. & Swan, J.W. 2019 Fast Stokesian dynamics. J. Fluid Mech. 878, 544–597.CrossRefGoogle Scholar
Forterre, Y. 2022 Basic soft matter for plants. In Soft Matter in Plants: From Biophysics to Biomimetics (ed. Jensen, K. & Forterre, Y.), pp. 1–65. The Royal Society of Chemistry.Google Scholar
Fu, H.C., Shenoy, V.B. & Powers, T.R. 2008 Role of slip between a probe particle and a gel in microrheology. Phys. Rev. E 78 (6), 061503.CrossRefGoogle Scholar
Fu, H.C., Shenoy, V.B. & Powers, T.R. 2010 Low-Reynolds-number swimming in gels. Europhys. Lett. 91 (2), 24002.CrossRefGoogle Scholar
Happel, J. & Brenner, H. 2012 Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media, vol. 1. Springer Science & Business Media.Google Scholar
Ho, B.P. & Leal, L.G. 1974 Inertial migration of rigid spheres in two-dimensional unidirectional flows. J. Fluid Mech. 65 (2), 365–400.CrossRefGoogle Scholar
Hobson, C.M., Falvo, M.R. & Superfine, R. 2021 A survey of physical methods for studying nuclear mechanics and mechanobiology. APL Bioengng 5 (4), 041508.CrossRefGoogle Scholar
Howard, J. 2001 Mechanics of Motor Proteins and the Cytoskeleton. Sinauer Associates.Google Scholar
Hu, H.H. & Joseph, D.D. 1999 Lift on a sphere near a plane wall in a second-order fluid. J. Non-Newtonian Fluid Mech. 88 (1-2), 173–184.CrossRefGoogle Scholar
Jiang, H. & Sun, S.X. 2013 Cellular pressure and volume regulation and implications for cell mechanics. Biophys. J. 105 (3), 609–619.CrossRefGoogle Scholar
Kalukula, Y., Stephens, A.D., Lammerding, J. & Gabriele, S. 2022 Mechanics and functional consequences of nuclear deformations. Nat. Rev. Mol. Cell Biol. 23 (9), 583–602.CrossRefGoogle Scholar
Keren, K., Yam, P.T., Kinkhabwala, A., Mogilner, A. & Theriot, J.A. 2009 Intracellular fluid flow in rapidly moving cells. Nat. Cell Biol. 11 (10), 1219–1224.CrossRefGoogle Scholar
Khair, A.S. & Squires, T.M. 2010 Active microrheology: a proposed technique to measure normal stress coefficients of complex fluids. Phys. Rev. Lett. 105 (15), 156001.CrossRefGoogle Scholar
Kim, S. & Karrila, S.J. 2013 Microhydrodynamics: Principles and Selected Applications. Courier Corporation.Google Scholar
Koch, D.L. & Subramanian, G. 2006 The stress in a dilute suspension of spheres suspended in a second-order fluid subject to a linear velocity field. J. Non-Newtonian Fluid Mech. 138 (2–3), 87–97.CrossRefGoogle Scholar
Lauga, E. & Powers, T.R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72 (096601), 096601.CrossRefGoogle Scholar
Leal, L.G. 1980 Particle motions in a viscous fluid. Annu. Rev. Fluid Mech. 12 (1), 435–476.CrossRefGoogle Scholar
Levine, A.J. & Lubensky, T.C. 2000 One-and two-particle microrheology. Phys. Rev. Lett. 85 (8), 1774.CrossRefGoogle Scholar
Levine, A.J. & Lubensky, T.C. 2001 Response function of a sphere in a viscoelastic two-fluid medium. Phys. Rev. E 63 (4), 041510.CrossRefGoogle Scholar
Lévy, T. 1983 Fluid flow through an array of fixed particles. Intl J. Engng Sci. 21 (1), 11–23.CrossRefGoogle Scholar
Li, G., Lauga, E. & Ardekani, A.M. 2021 Microswimming in viscoelastic fluids. J. Non-Newtonian Fluid Mech. 297, 104655.CrossRefGoogle Scholar
Marchetti, M.C., Joanny, J.-F., Ramaswamy, S., Liverpool, T.B., Prost, J., Rao, M. & Simha, R.A. 2013 Hydrodynamics of soft active matter. Rev. Mod. Phys. 85 (3), 1143.CrossRefGoogle Scholar
Masoud, H. & Stone, H.A. 2014 A reciprocal theorem for Marangoni propulsion. J. Fluid Mech. 741, R4.CrossRefGoogle Scholar
Masoud, H. & Stone, H.A. 2019 The reciprocal theorem in fluid dynamics and transport phenomena. J. Fluid Mech. 879, P1.CrossRefGoogle Scholar
Mitchison, T.J., Charras, G.T. & Mahadevan, L. 2008 Implications of a poroelastic cytoplasm for the dynamics of animal cell shape. In Seminars in Cell & Developmental Biology, vol. 19, pp. 215–223. Elsevier.Google Scholar
Moeendarbary, E., Valon, L., Fritzsche, M., Harris, A.R., Moulding, D.A., Thrasher, A.J., Stride, E., Mahadevan, L. & Charras, G.T. 2013 The cytoplasm of living cells behaves as a poroelastic material. Nat. Mater. 12 (3), 253.CrossRefGoogle Scholar
Mogre, S.S., Brown, A.I. & Koslover, E.F. 2020 Getting around the cell: physical transport in the intracellular world. Phys. Biol. 17 (6), 061003.CrossRefGoogle Scholar
Moradi, M., Shi, W. & Nazockdast, E. 2022 General solutions of linear poro-viscoelastic materials in spherical coordinates. J. Fluid Mech. 946, A22.CrossRefGoogle Scholar
Nezamabadi, S., Zahrouni, H. & Yvonnet, J. 2011 Solving hyperelastic material problems by asymptotic numerical method. Comput. Mech. 47 (1), 77–92.CrossRefGoogle Scholar
Papavassiliou, D. & Alexander, G.P. 2015 The many-body reciprocal theorem and swimmer hydrodynamics. Europhys. Lett. 110 (4), 44001.CrossRefGoogle Scholar
Phan-Thien, N. & Kim, S. 1994 Microstructures in Elastic Media: Principles and Computational Methods. Oxford University Press.CrossRefGoogle Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.CrossRefGoogle Scholar
Pozrikidis, C. 2002 A Practical Guide to Boundary Element Methods with the Software Library BEMLIB. CRC Press.CrossRefGoogle Scholar
Predeleanu, M. 1984 Development of boundary element method to dynamic problems for porous media. Appl. Math. Model. 8 (6), 378–382.CrossRefGoogle Scholar
Saintillan, D. & Shelley, M.J. 2015 Theory of active suspensions. In Complex Fluids in Biological Systems: Experiment, Theory, and Computation, pp. 319–355. Springer.CrossRefGoogle Scholar
Shankar, S. & Mahadevan, L. 2022 Active muscular hydraulics. bioRxiv 2022–02.Google Scholar
Simon, B.R. 1992 Multiphase poroelastic finite element models for soft tissue structures. Appl. Mech. Rev. 45 (6), 191–218.CrossRefGoogle Scholar
Stone, H.A. & Samuel, A.D.T. 1996 Propulsion of microorganisms by surface distortions. Phys. Rev. Lett. 77 (19), 4102.CrossRefGoogle Scholar
Strychalski, W., Copos, C.A., Lewis, O.L. & Guy, R.D. 2015 A poroelastic immersed boundary method with applications to cell biology. J. Comput. Phys. 282, 77–97.CrossRefGoogle Scholar
Swan, J.W., Brady, J.F., Moore, S., et al. 2011 Modeling hydrodynamic self-propulsion with Stokesian dynamics. or teaching Stokesian dynamics to swim. Phys. Fluids 23 (7), 017901.CrossRefGoogle Scholar
Weihs, D., Mason, T.G. & Teitell, M.A. 2006 Bio-microrheology: a frontier in microrheology. Biophys. J. 91 (11), 4296–4305.CrossRefGoogle Scholar