Article contents
Rayleigh–Taylor unstable condensing liquid layers with nonlinear effects of interfacial convection and diffusion of vapour
Published online by Cambridge University Press: 06 October 2020
Abstract
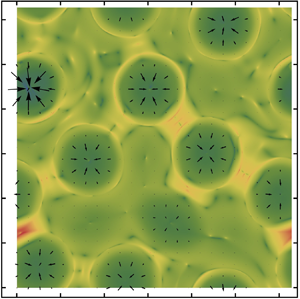
We investigate the three-dimensional surface pattern and nonlinear dynamics of a condensing liquid layer suspended from a cooled substrate and in contact with a mixture of its vapour and an inert gas below. A vapour boundary layer (VBL) is introduced, to which the changes in gaseous composition and temperature are assumed to be confined. An interfacial transport equation is derived, which incorporates the physical effects of convection and diffusion of vapour within the VBL, coupled with a long-wave evolution equation for the location of the free surface. This work extends the study of Kanatani (J. Fluid Mech., vol. 732, 2013, pp. 128–149) on a sessile evaporating film to the Rayleigh–Taylor unstable condensing/evaporating case with nonlinear analyses which also accounts for the effect of vapour recoil due to mass transfer on interfacial evolution and that of gravity combined with buoyancy on the internal convection of pendent drops in a condensate layer. The coupled nonlinear evolutionary system is referred to as a  $1.5$-sided model. It can be reduced to the conventional one-sided model when phase change is limited by processes in the liquid. An extended basic state is obtained, whose stability is investigated with pseudo-steady linear theory and time-dependent nonlinear simulations. With the one-sided model, the influences of vapour recoil and Marangoni effects are illustrated with three representative cases. In the one-sided simulations with a random perturbation, the interface is prone to finite-time rupture and the surface patterns feature isolated droplets when vapour recoil is significant, while it becomes more regular and even without rupture as vapour recoil is weakened relative to the Marangoni effect. This suggests that, in the absence of the convection and diffusion of vapour, the destabilizations of vapour recoil and negative gravity could prevail over the stabilizations of thermocapillarity, capillarity, viscous dissipation and mass gain. With an unsaturated initial interface concentration,
$1.5$-sided model. It can be reduced to the conventional one-sided model when phase change is limited by processes in the liquid. An extended basic state is obtained, whose stability is investigated with pseudo-steady linear theory and time-dependent nonlinear simulations. With the one-sided model, the influences of vapour recoil and Marangoni effects are illustrated with three representative cases. In the one-sided simulations with a random perturbation, the interface is prone to finite-time rupture and the surface patterns feature isolated droplets when vapour recoil is significant, while it becomes more regular and even without rupture as vapour recoil is weakened relative to the Marangoni effect. This suggests that, in the absence of the convection and diffusion of vapour, the destabilizations of vapour recoil and negative gravity could prevail over the stabilizations of thermocapillarity, capillarity, viscous dissipation and mass gain. With an unsaturated initial interface concentration,  $\tilde {x}_{A,I0}$, the
$\tilde {x}_{A,I0}$, the  $1.5$-sided model indicates that the liquid layer can be stabilized to a quasi-hexagon pattern and the Rayleigh–Taylor-driven rupture can be suppressed with the effects of vapour convection and diffusion near the interface. However, the initial dynamics is in contrast to the case with a saturated
$1.5$-sided model indicates that the liquid layer can be stabilized to a quasi-hexagon pattern and the Rayleigh–Taylor-driven rupture can be suppressed with the effects of vapour convection and diffusion near the interface. However, the initial dynamics is in contrast to the case with a saturated  $\tilde {x}_{A,I0}$, where transition from weak evaporation to a condensation-dominated regime is seen in the later stage. The viewpoint of stability competition offers vital evidence for an induced Marangoni stabilization, which is a quintessential characteristic of the
$\tilde {x}_{A,I0}$, where transition from weak evaporation to a condensation-dominated regime is seen in the later stage. The viewpoint of stability competition offers vital evidence for an induced Marangoni stabilization, which is a quintessential characteristic of the  $1.5$-sided model. Comparisons of the theory and simulations with available experiments are included throughout.
$1.5$-sided model. Comparisons of the theory and simulations with available experiments are included throughout.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 2
- Cited by



