Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T14:51:36.744Z Has data issue: false hasContentIssue false
  • English
  • Français

Radial lift on a suspended finite-sized sphere due to fluid inertia for low-Reynolds-number flow through a cylinder

Published online by Cambridge University Press:  28 March 2013

Sukalyan Bhattacharya ,
Dil K. Gurung  and
Shahin Navardi
Sukalyan Bhattacharya*
Affiliation:
Department of Mechanical Engineering Texas Tech University, Lubbock, TX 79409, USA
Dil K. Gurung
Affiliation:
Department of Mechanical Engineering Texas Tech University, Lubbock, TX 79409, USA
Shahin Navardi
Affiliation:
Department of Mechanical Engineering Texas Tech University, Lubbock, TX 79409, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This article describes the radial drift of a suspended sphere in a cylinder-bound Poiseuille flow where the Reynolds number is small but finite. Unlike past studies, it considers a circular narrow conduit whose cross-sectional diameter is only 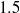$1. 5$–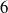$6$ times the particle diameter. Thus, the analysis quantifies the effect of fluid inertia on the radial motion of the particle in the channel when the flow field is significantly influenced by the presence of the suspended body. To this end, the hydrodynamic fields are expanded as a series in Reynolds number, and a set of hierarchical equations for different orders of the expansion is derived. Accordingly, the zeroth-order fields in Reynolds number satisfy the Stokes equation, which is accurately solved in the presence of the spherical particle and the cylindrical conduit. Then, recognizing that in narrow vessels Stokesian scattered fields from the sphere decrease exponentially in the axial direction, a simpler regular perturbation scheme is used to quantify the first-order inertial correction to hydrodynamic quantities. Consequently, it is possible to obtain two results. First, the sphere is assumed to follow the axial motion of a freely suspended sphere in a Stokesian condition, and the radial lift force on it due to the presence of fluid inertia is evaluated. Then, the approximate motion is determined for a freely suspended body on which net hydrodynamic force including first-order inertial lift is zero. The results agree well with the available experimental results. Thus, this study along with the measured data would precisely describe particle dynamics inside narrow tubes.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 722 , 10 May 2013 , pp. 159 - 186
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmolov, E. S. 1999 The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number. J. Fluid Mech. 381, 63–87.Google Scholar
Betherton, F. P. 1962 The motion of rigid particles in a shear flow at low Reynolds number. J. Fluid Mech. 14, 284–304.CrossRefGoogle Scholar
Bhattacharya, S. 2005 Unsteady hydrodynamic effect of rotation on steady rigid body motion. J. Fluid Mech. 538, 291–308.Google Scholar
Bhattacharya, S. 2008 History force on an asymmetrically rotating body in Poiseuille flow inducing particle-migration across a slit-pore. Phys. Fluids 20, 093301.CrossRefGoogle Scholar
Bhattacharya, S., Mishra, C. & Bhattacharya, S. 2010 Analysis of general creeping motion of a sphere inside a cylinder. J. Fluid Mech. 642, 295–328.Google Scholar
Brenner, H. & Cox, R. G. 1963 The resistance to a particle of arbitary shape in translational motion at small Reynolds number. J. Fluid Mech. 17, 561–596.CrossRefGoogle Scholar
DiCarlo, D., Edd, J. F., Humphry, K. J., Stone, H. A. & Toner, M. 2009 Particle segregation and dynamics in confined flows. Phys. Rev. Lett. 102, 094503.Google Scholar
Halow, J. S. & Wills, G. B. 1970 Radial migration of spherical particles in Couette systems. AIChE J. 16, 281–286.Google Scholar
Ho, B. P. & Leal, L. G. 1974 Inertial migration of rigid spheres in two-dimensional unidirectional flows. J. Fluid Mech. 65, 365–400.Google Scholar
Jendrejack, R. M, Schwartz, D. C., de Pablo, J. J. & Graham, M. D. 2004 Shear-induced migration in flowing polymer solutions: simulation of long-chain DNA in microchannels. J. Chem. Phys. 120, 2513–2529.Google Scholar
Liao, J. C., Hein, T. W., Vaughn, M. W., Huang, K. T. & Kuo, L. 1999 Intravascular flow decreases erythrocyte consumption of nitric oxide. Proc. Natl Acad. Sci. 96, 8757–8761.Google Scholar
Liron, N. & Mochon, S. 1976 Stokes flow for a Stokeslet between two parallel flat plates. J. Engng Maths 10, 287–303.Google Scholar
Lovalenti, P. M. & Brady, J. F. 1993 The hydrodynamic force on a rigid particle undergoing arbitary time dependent motion at small Reynolds number. J. Fluid Mech. 256, 561–605.Google Scholar
Matas, J. P., Morris, J. F. & Guazzelli, E. 2004 Inertial migration of rigid spherical particles in Poiseuille flow. J. Fluid Mech. 515, 171–195.Google Scholar
Matas, J. P., Morris, J. F. & Guazzelli, E. 2009 Lateral force on a rigid sphere in large-inertia laminar pipe flow. J. Fluid Mech. 621, 59–67.Google Scholar
Navardi, S. & Bhattacharya, S. 2010a A new lubrication theory to derive far-field axial pressure-difference due to force singularities in cylindrical or annular vessels. J. Math. Phys. 51, 043102.Google Scholar
Navardi, S. & Bhattacharya, S. 2010b Axial pressure-difference between far-fields across a sphere in viscous flow bounded by a cylinder. Phys. Fluids. 22, 103306.CrossRefGoogle Scholar
Navardi, S. & Bhattacharya, S. 2010c Effect of confining conduit on effective viscosity of dilute colloidal suspension. J. Chem. Phys. 132, 114114.Google Scholar
Oliver, R. 1962 Influence of particle rotation on radial migration in the Poiseuille flow of suspensions. Nature 194, 1269–1271.Google Scholar
Repetti, R. V. & Leonard, E. F. 1964 Segre–Silberberg annulus formation: a possible explanation. Nature 194, 1346–1348.CrossRefGoogle Scholar
Rubinow, S. I. & Keller, J. B. 1961 The transverse force on a spinning sphere moving in a viscous fluid. J. Fluid Mech. 15, 447–459.Google Scholar
Saffman, P. G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22, 385.Google Scholar
Saintillan, D., Shaqfeh, E. S. G. & Darve, E. 2006 Effect of flexibility on the shear-induced migration of short-chain polymers in parabolic channel flow. J. Fluid Mech. 557, 297–306.Google Scholar
Schonberg, J. A. & Hinch, E. J. 1989 Inertial migration of a sphere in Poiseuille flow. J. Fluid Mech. 203, 517–524.Google Scholar
Segre, G. & Silberberg, A. 1962a Behaviour of macroscopic rigid spheres in Poiseuille flow Part 1. J. Fluid Mech. 14, 115–135.Google Scholar
Segre, G. & Silberberg, A. 1962b Behaviour of macroscopic rigid spheres in Poiseuille flow Part 2. J. Fluid Mech. 14, 136–157.Google Scholar
Shao, X., Yu, Z. & Sun, B. 2008 Inertial migration of spherical particles in circular Poiseuille flow at moderately high Reynolds numbers. Phys. Fluids 20, 103307.CrossRefGoogle Scholar
Stadler, A., Zilow, E. & Linderkamp, O. 1990 Blood viscocity and optimal hematocrit in narrow tubes. Biorheology 27, 779–788.Google Scholar
Tachibana, M. 1973 On the behaviour of a sphere in the laminar tube flows. Rheol. Acta 12, 58–69.CrossRefGoogle Scholar