Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T22:54:20.046Z Has data issue: false hasContentIssue false
  • English
  • Français

The quiescent core of turbulent channel flow

Published online by Cambridge University Press:  18 June 2014

Y. S. Kwon ,
J. Philip ,
C. M. de Silva ,
N. Hutchins  and
J. P. Monty
Y. S. Kwon*
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
J. Philip
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
C. M. de Silva
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
N. Hutchins
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
J. P. Monty
Affiliation:
Department of Mechanical Engineering, The University of Melbourne, Victoria 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

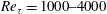The identification of uniform momentum zones in wall-turbulence, introduced by Adrian, Meinhart & Tomkins (J. Fluid Mech., vol. 422, 2000, pp. 1–54) has been applied to turbulent channel flow, revealing a large ‘core’ region having high and uniform velocity magnitude. Examination of the core reveals that it is a region of relatively weak turbulence levels. For channel flow in the range $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}Re_{\tau } = 1000\text {--}4000$, it was found that the ‘core’ is identifiable by regions bounded by the continuous isocontour lines of the streamwise velocity at 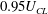$0.95U_{CL}$ (95 % of the centreline velocity). A detailed investigation into the properties of the core has revealed it has a large-scale oscillation which is predominantly anti-symmetric with respect to the channel centreline as it moves through the channel, and there is a distinct jump in turbulence statistics as the core boundary is crossed. It is concluded that the edge of the core demarcates a shear layer of relatively intense vorticity such that the interior of the core contains weakly varying, very low-level turbulence (relative to the flow closer to the wall). Although channel flows are generally referred to as ‘fully turbulent’, these findings suggest there exists a relatively large and ‘quiescent’ core region with a boundary qualitatively similar to the turbulent/non-turbulent interface of boundary layers, jets and wakes.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 751 , 25 July 2014 , pp. 228 - 254
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Antonia, R. A., Teitel, M., Kim, J. & Browne, L. W. B. 1992 Low-Reynolds-number effects in a fully developed turbulent channel flow. J. Fluid Mech. 236, 579–605.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. A 365, 665–681.CrossRefGoogle ScholarPubMed
Bernal, P. & Roshko, A. 1986 Streamwise vortex structure in plane mixing layers. J. Fluid Mech. 170, 499–525.CrossRefGoogle Scholar
Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.CrossRefGoogle Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.Google Scholar
Chauhan, K., Philip, J., de Silva, C., Hutchins, N. & Marusic, I. 2014 The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.CrossRefGoogle Scholar
Corrsin, S. & Kistler, A. L. 1955 Free-stream boundaries of turbulent flows. NACA Rep. 1244, 1033–1064.Google Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46, 567–590.Google Scholar
da Silva, C. B. & Pereira, J. C. F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/non-turbulent interface in jets. Phys. Fluids 20, 055101.Google Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Dean, R. B. & Bradshaw, P. 1976 Measurements of interacting turbulent shear layers in a duct. J. Fluid Mech. 78, 641–676.Google Scholar
de Silva, C. M., Baidya, R., Khashehchi, M. & Marusic, I. 2012 Assessment of tomographic PIV in wall-bounded turbulence using direct numerical simulation data. Exp. Fluids 52 (2), 425–440.Google Scholar
del Alamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Hunt, J. C. R., Eames, I., da Silva, C. B. & Westerweel, J. 2011 Interfaces and inhomogeneous turbulence. Phil. Trans. R. Soc. A 369, 811–832.Google Scholar
Hunt, J. C. R. & Morrison, J. F. 2001 Eddy structure in turbulent boundary layers. Eur J. Mech. (B Fluids) 19, 673–694.CrossRefGoogle Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel flow. J. Fluid Mech. 205, 421–451.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41, 283–325.Google Scholar
Lofquist, K. 1960 Flow and stress near an interface between stratified liquids. Phys. Fluids 3, 158–175.Google Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7, 694–696.Google Scholar
Monty, J. P.2005 Development in smooth wall turbulent duct flows. PhD thesis, The University of Melbourne.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Ng, H. C.2011 Experiments in smooth wall turbulent channel and pipe flows. PhD thesis, The University of Melbourne.Google Scholar
Roth, G. I. & Katz, J. 2001 Five techniques for increasing the speed and accuracy of PIV interrogation. Meas. Sci. Technol. 12, 238–245.Google Scholar
Sabot, J. & Comte-Bellot, G. 1976 Intermittency of coherent structures in the core region of fully developed turbulent pipe flow. J. Fluid Mech. 74, 767–796.Google Scholar
Semin, N. V., Golub, V. V., Elsinga, G. E. & Westerweel, J. 2011 Laminar superlayer in a turbulent boundary layer. Tech. Phys. Lett. 37, 1154–1157.CrossRefGoogle Scholar
Silva, R. A. & de Lemos, M. J. S. 2003 Turbulent flow in a channel occupied by a porous layer considering the stress jump at the interface. Intl J. Heat Mass Transfer 46, 5113–5121.Google Scholar
Teitel, M. & Antonia, R. A. 1990 The interaction region of a turbulent duct flow. Phys. Fluids A 2 (5), 808–813.Google Scholar
Townsend, A. A. 1948 Local isotropy in the turbulent wake of a cylinder. Austral. J. Sci. Res. A 1, 161–174.Google Scholar
Townsend, A. A. 1956 The Structure of Turbulent Shear Flow, 1st edn. Cambridge University Press.Google Scholar
Westerweel, J., Hofmann, T., Fukushima, C. & Hunt, J. C. R. 2002 The turbulent/non-turbulent interface at the outer boundary of a self-similar turbulent jet. Exp. Fluids 33, 873–878.Google Scholar