Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T04:04:26.774Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-geostrophic shallow-water doubly-connected vortex equilibria and their stability

Published online by Cambridge University Press:  16 April 2013

Hanna Płotka  and
David G. Dritschel
Hanna Płotka*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews, Fife KY16 9SS, UK
David G. Dritschel
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews, Fife KY16 9SS, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the form, properties, stability and evolution of doubly-connected (two-vortex) relative equilibria in the single-layer 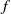$f$-plane quasi-geostrophic shallow-water model of geophysical fluid dynamics. Three parameters completely describe families of equilibria in this system: the ratio 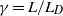$\gamma = L/ {L}_{D} $ between the horizontal size of the vortices and the Rossby deformation length; the area ratio $\alpha $ of the smaller to the larger vortex; and the minimum distance 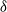$\delta $ between the two vortices. We vary 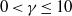$0\lt \gamma \leq 10$ and 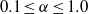$0. 1\leq \alpha \leq 1. 0$, determining the boundary of stability 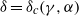$\delta = {\delta }_{c} (\gamma , \alpha )$. We also examine the nonlinear development of the instabilities and the transitions to other near-equilibrium configurations. Two modes of instability occur when 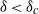$\delta \lt {\delta }_{c} $: a small-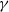$\gamma $ asymmetric (wave 3) mode, which is absent for 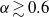$\alpha \gtrsim 0. 6$; and a large-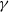$\gamma $ mode. In general, major structural changes take place during the nonlinear evolution of the vortices, which near 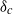${\delta }_{c} $ may be classified as follows: (i) vacillations about equilibrium for 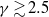$\gamma \gtrsim 2. 5$; (ii) partial straining out, associated with the small-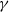$\gamma $ mode, where either one or both of the vortices get smaller for 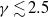$\gamma \lesssim 2. 5$ and 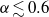$\alpha \lesssim 0. 6$; (iii) partial merger, occurring at the transition region between the two modes of instability, where one of the vortices gets bigger, and (iv) complete merger, associated with the large-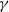$\gamma $ mode. We also find that although conservative inviscid transitions to equilibria with the same energy, angular momentum and circulation are possible, they are not the preferred evolutionary path.

JFM classification

Vortex Flows: Contour dynamics Geophysical and Geological Flows: Rotating flows Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 723 , 25 May 2013 , pp. 40 - 68
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alejo, M. A. 2012 Geometric breathers of the mKdV equation. Acta Appl. Maths 121, 137–155.CrossRefGoogle Scholar
Carton, X. 2001 Hydrodynamical modelling of oceanic vortices. Surv. Geophys. 22, 179–263.Google Scholar
Cerretelli, C. & Williamson, C. H. K. 2003a The physical mechanism for vortex merging. J. Fluid Mech. 475, 41–77.CrossRefGoogle Scholar
Cerretelli, C. & Williamson, C. H. K. 2003b A new family of uniform vortices related to vortex configurations before merging. J. Fluid Mech. 493, 219–229.Google Scholar
Charney, J. G. & Flierl, G. R. 1981 Oceanic analogues of large-scale atmospheric motions. In Evolution of Physical Oceanography (ed. Warren, B. A. & Wunsch, C.), pp. 504–548. MIT.Google Scholar
Deem, G. S. & Zabusky, N. J. 1978a Stationary V-states, interactions, recurrence, and breaking. In Solitons in Action (ed. Longren, K. & Scott, A.), pp. 277–293. Academic.Google Scholar
Deem, G. S. & Zabusky, N. J. 1978b Vortex waves: stationary V-states, interactions, recurrence, and breaking. Phys. Rev. Lett. 40, 859–862.Google Scholar
Dritschel, D. G. 1985 The stability and energetics of corotating uniform vortices. J. Fluid Mech. 157, 95–134.Google Scholar
Dritschel, D. G. 1986 The nonlinear evolution of rotating configurations of uniform vorticity. J. Fluid Mech. 172, 157–182.CrossRefGoogle Scholar
Dritschel, D. G. 1988 Contour surgery: a topological reconnection scheme for extended integrations using contour dynamics. J. Comput. Phys. 77, 240–266.CrossRefGoogle Scholar
Dritschel, D. G. 1989 Contour dynamics and contour surgery: numerical algorithms for extended, high-resolution modelling of vortex dynamics in two-dimensional, inviscid, incompressible flows. Comput. Phys. Rep. 10, 77–146.CrossRefGoogle Scholar
Dritschel, D. G. 1993 Vortex properties of two-dimensional turbulence. Phys. Fluids A 5, 984–997.Google Scholar
Dritschel, D. G. 1995 A general theory for two-dimensional vortex interactions. J. Fluid Mech. 293, 269–303.CrossRefGoogle Scholar
Dritschel, D. G. & Legras, B. 1991 The elliptical model of two-dimensional vortex dynamics. Part II: disturbance equations. Phys. Fluids A 3, 855–868.CrossRefGoogle Scholar
Dritschel, D. G., Scott, R. K., Macaskill, C., Gottwald, G. A. & Tran, C. V. 2008 Unifying scaling theory for vortex dynamics in two-dimenisional turbulence. Phys. Rev. Lett. 101, 094501.CrossRefGoogle Scholar
Dritschel, D. G. & Waugh, D. W. 1992 Quantification of the inelastic interaction of unequal vortices in two-dimensional vortex dynamics. Phys. Fluids A 4, 1737–1744.Google Scholar
Fontane, J. & Dritschel, D. G. 2009 The HyperCASL algorithm: a new approach to the numerical simulation of geophysical flows. J. Comput. Phys. 228, 6411–6425.Google Scholar
Fornberg, B. 1977 A numerical study of 2-d turbulence. J. Comput. Phys. 25, 1–31.Google Scholar
Ghil, M., Feliks, Y. & Sushama, L. U. 2002 Baroclinic and barotropic aspects of the wind-driven ocean circulation. Physica D 167 (1–2), 1–35.Google Scholar
Griffiths, R. W. & Hopfinger, E. J. 1986 Experiments with baroclinic vortex pairs in a rotating fluid. J. Fluid Mech. 173, 501–518.CrossRefGoogle Scholar
Griffiths, R. W. & Hopfinger, E. J. 1987 Coalescence of geostrophic vortices. J. Fluid Mech. 178, 73–97.CrossRefGoogle Scholar
Hoskins, B. J., McIntyre, M. E. & Robertson, R. W. 1985 On the use and significance of isentropic potential vorticity maps. Q. J. R. Meteorol Soc. 111, 877–946.CrossRefGoogle Scholar
Legras, B. & Dritschel, D. G. 1993 Vortex stripping and the generation of high vorticity gradients in two dimensional flows. Appl. Sci. Res. 51, 445–455.Google Scholar
Legras, B., Dritschel, D. G. & Caillol, P. 2001 The erosion of a distributed two-dimensional vortex in a background straining flow. J. Fluid Mech. 441, 369–398.Google Scholar
Luzzatto-Fegiz, P. & Williamson, C. H. K. 2012 Determining the stability of steady two-dimensional flows through imperfect velocity-impulse diagrams. J. Fluid Mech. 706, 323–350.Google Scholar
Makarov, V. G. & Kizner, Z. 2011 Stability and evolution of uniform-vorticity dipoles. J. Fluid Mech. 672, 307–325.Google Scholar
Makarov, V. G., Sokolovskiy, M. A. & Kizner, Z. 2012 Doubly symmetric finite-core heton equilibria. J. Fluid Mech. 708, 397–417.Google Scholar
Mariotti, A., Legras, B. & Dritschel, D. G. 1994 Vortex stripping and the erosion of coherent structures in two dimensional flows. Phys. Fluids 6, 3954–3962.CrossRefGoogle Scholar
McIntyre, M. E. 1993 The middle atmosphere: atmospheric dynamics – some fundamentals, with observational implications. In The Use of EOS for Studies of Atmospheric Physics (ed. Gille, J. C. & Visconti, G.), Proc. Intl School of Physics ‘Enrico Fermi’ CXV Course, pp. 313–386. North-Holland.Google Scholar
McWilliams, J. C. 1984 The emergence of isolated coherent vortices in turbulent flow. J. Fluid Mech. 146, 21–43.Google Scholar
Melander, M. V., Zabusky, N. J. & McWilliams, J. C. 1987 Asymmetric vortex merger in two-dimensions: which vortex is ‘victorious’?. Phys. Fluids 30, 2610–2612.Google Scholar
Meunier, P. & Leweke, T. 2001 Three-dimensional instability during vortex merging. Phys. Fluids 13, 2747–2750.Google Scholar
Mitchell, T. B. & Driscoll, C. F. 1996 Electron vortex orbits and merger. Phys. Fluids 8, 1828–1841.Google Scholar
Nycander, J., Dritschel, D. G. & Sutyrin, G. G. 1993 The dynamics of long frontal waves in the shallow water equations. Phys. Fluids A 5, 1089–1091.CrossRefGoogle Scholar
Pedlosky, J. 1979 Geophysical Fluid Dynamics. Springer.CrossRefGoogle Scholar
Pierrehumbert, R. T. 1980 A family of steady, translating vortex pairs with distributed vorticity. J. Fluid Mech. 99, 129–144.Google Scholar
Płotka, H. & Dritschel, D. G. 2012 Quasi-geostrophic shallow-water vortex-patch equilibria and their stability. Geophys. Astrophys. Fluid 106 (6), 574–595.CrossRefGoogle Scholar
Polvani, L. M. 1988 Geostrophic vortex dynamics. PhD thesis, MIT/WHOI WHOI-88-48.Google Scholar
Polvani, L. M. 1991 Two-layer geostrophic vortex dynamics. Part 2. Alignment and two-layer V-states. J. Fluid Mech. 225, 241–270.Google Scholar
Polvani, L. M. C., McWilliams, J., Spall, M. A. & Ford, R. 1994 The coherent structures of shallow-water turbulence: deformation-radius effects, cyclone/anticyclone asymmetry and gravity-wave generation. Chaos 4 (2), 177–186.Google Scholar
Polvani, L. M., Zabusky, N. J. & Flierl, G. R. 1989 Two-layer geostrophic vortex dynamics. Part 1. Upper-layer V-states and merger. J. Fluid Mech. 205, 215–242.Google Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Saffman, P. G. & Szeto, R. 1980 Equilibrium shapes of a pair of equal uniform vortices. Phys. Fluids 23, 2339–2342.Google Scholar
Santangelo, R., Benzi, R. & Legras, B. 1989 The generation of vortices in high-resolution, two-dimensional decaying turbulence and the influence of initial conditions on the breaking of self-similarity. Phys. Fluids A 1, 1027–1034.CrossRefGoogle Scholar
Scott, R. K. & Polvani, L. M. 2008 Equatorial superrotation in shallow atmospheres. Geophys. Res. Lett. 35, L24202.CrossRefGoogle Scholar
Trieling, R. R., Fuentes, O. U. & van Heijst, G. J. 2005 Interaction of two unequal corotating vortices. Phys. Fluids 17, 087103.Google Scholar
Viúdez, Á. & Dritschel, D. G. 2004 Dynamic potential vorticity initialization and the diagnosis of mesoscale motion. J. Phys. Oceanogr. 34, 2761–2773.Google Scholar
Waugh, D. W. 1992 The efficiency of symmetric vortex merger. Phys. Fluids A 4, 1745–1758.Google Scholar
Waugh, D. W. & Dritschel, D. G. 1991 The stability of filamentary vorticity in two-dimensional geophysical vortex-dynamics models. J. Fluid Mech. 231, 575–598.Google Scholar
Wu, H. M., Overman, E. A. II & Zabusky, N. J. 1985 Steady-state solutions of the Euler equations in two dimensions: rotating and translating V-states with limiting cases. I. Numerical algorithms and results. J. Comput. Phys. 53, 42–71.Google Scholar
Yasuda, I. 1995 Geostrophic vortex merger and streamer development in the ocean with special reference to the merger of Kuroshio warm core rings. J. Phys. Oceanogr. 25, 979–996.Google Scholar
Yasuda, I. & Flierl, G. R. 1995 Two-dimensional asymmetric vortex merger: contour dynamics experiment. J. Phys. Oceanogr. 51, 145–170.CrossRefGoogle Scholar
Zabusky, N. J., Hughes, M. H. & Roberts, K. V. 1979 Contour dynamics for the Euler equations in two dimensions. J. Comput. Phys. 30, 96–106.Google Scholar

Płotka and Dritschel supplementary movies

Examples of doubly-connected vortex equilibria for °=0.02, 3, and 10 at Arat = 0.2. For each case we begin at the distance ± = 0.8, and end at the smallest distance attained, ± = ±f (°), at which a sharp corner develops on the boundary of one of the vortices. The smallest distance decreases with °. In this and subsequent movies we are in a frame of reference rotating with the equilibria, and |x|, |y| 6 3.

Download Płotka and Dritschel supplementary movies(Video)
Video 927.3 KB

Płotka and Dritschel supplementary movies

An example of the evolution of a state undergoing partial straining out PSOb. We show the case ° = 1, Arat = 0.4, and ± = 0.339, for times between 88.47Tp and 132.71Tp.

Download Płotka and Dritschel supplementary movies(Video)
Video 2.8 MB

Płotka and Dritschel supplementary movies

An example of the evolution of a state undergoing partial merger PM. We show the case ° = 2, Arat = 0.6, and ± = 0.270, for times between 150.28Tp and 254.31Tp.

Download Płotka and Dritschel supplementary movies(Video)
Video 8.9 MB

Płotka and Dritschel supplementary movies

An example of the evolution of a state having large ° which undergoes complete merger CM. We show the case ° = 10, Arat = 0.2, and ± = 0.268, for times between 121.70Tp and 135.22Tp.

Download Płotka and Dritschel supplementary movies(Video)
Video 2.5 MB

Płotka and Dritschel supplementary movies

An example of the evolution of a state having small ° which undergoes complete merger CM. We show the case ° = 0.02, Arat = 1.0, and ± = 0.266, for times between 33.50Tp and 100.49Tp.

Download Płotka and Dritschel supplementary movies(Video)
Video 17.9 MB

Płotka and Dritschel supplementary movies

An example of the evolution of a state undergoing vacillations. We show the case ° = 10, Arat = 0.4, and ± = 0.200, for times between 0 and 115.68Tp. Note, the boundary of stability occurs at ± = ±c = 0.265.

Download Płotka and Dritschel supplementary movies(Video)
Video 1.9 MB