Article contents
Quadrupolar flows around spots in internal shear flows
Published online by Cambridge University Press: 06 April 2020
Abstract
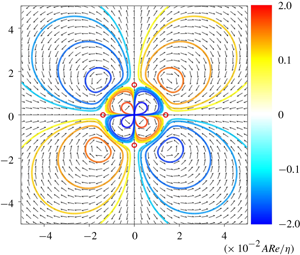
Turbulent spots occur in shear flows confined between two walls and are surrounded by robust quadrupolar flows. Although the far-field decay of such large-scale flows has been reported to be exponential, we predict a different algebraic decay for the case of plane Couette flow. We address this problem theoretically, by modelling an isolated spot as an obstacle in a linear plane shear flow with free-slip boundary conditions at the walls. By seeking invariant solutions in a co-moving Lagrangian frame and using geometric scale separation, a set of differential equations governing large-scale flows is derived from the Navier–Stokes equations and solved analytically. The wall-normal velocity turns out to be exponentially localised in the plane, while the quadrupolar in-plane velocity field, after wall-normal averaging, features a superposition of algebraic and exponential decays. The algebraic decay exponent is  $-3$. The quadrupolar angular dependence stems from (i) the shearing of the streamwise velocity and (ii) the breaking of the spanwise homogeneity. Near the spot, exponentially decaying solutions can generate reversed quadrupolar flows. Eventually, by noting that the algebraically decaying in-plane flow is two-dimensional and harmonic, we suggest a topological origin to the quadrupolar large-scale flow.
$-3$. The quadrupolar angular dependence stems from (i) the shearing of the streamwise velocity and (ii) the breaking of the spanwise homogeneity. Near the spot, exponentially decaying solutions can generate reversed quadrupolar flows. Eventually, by noting that the algebraically decaying in-plane flow is two-dimensional and harmonic, we suggest a topological origin to the quadrupolar large-scale flow.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 7
- Cited by


