Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T04:48:38.491Z Has data issue: false hasContentIssue false
  • English
  • Français

QNSE theory of turbulence anisotropization and onset of the inverse energy cascade by solid body rotation

Published online by Cambridge University Press:  20 September 2016

Semion Sukoriansky  and
Boris Galperin
Semion Sukoriansky
Affiliation:
Department of Mechanical Engineering, Ben-Gurion University of the Negev, Beer-Sheva 84105, Israel Perlstone Center for Aeronautical Engineering Studies, Beer-Sheva 84105, Israel
Boris Galperin*
Affiliation:
College of Marine Science, University of South Florida, St. Petersburg, FL 33701, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Under the action of solid body rotation, homogeneous neutrally stratified turbulence undergoes anisotropization and onset of the inverse energy cascade. These processes are investigated using a quasi-normal scale elimination (QNSE) theory in which successive coarsening of a flow domain yields scale-dependent eddy viscosity and diffusivity. The effect of rotation increases with increasing scale and manifests in anisotropization of the eddy viscosities, eddy diffusivities and kinetic energy spectra. 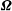Not only the vertical (in the direction of the vector of rotation $\unicode[STIX]{x1D734}$) and horizontal eddy viscosities and eddy diffusivities become different but, reflecting both directional and componental anisotropization, there emerge four different eddy viscosities. Three of them decrease relative to the eddy viscosity in non-rotating flows while one increases; the horizontal ‘isotropic’ viscosity decreases at the fastest rate. This behaviour is indicative of the increasing redirection of the energy flux to larger scales, the phenomenon that can be associated with the energy backscatter or inverse energy cascade. On scales comparable to the Woods’s scale which is the rotational analogue of the Ozmidov length scale in stably stratified flows, the horizontal viscosity rapidly decreases, and in order to keep it positive, a weak rotation limit is invoked. Within that limit, an analytical theory of the transition from the Kolmogorov to a rotation-dominated turbulence regime is developed. It is shown that the dispersion relation of linear inertial waves is unaffected by turbulence while all one-dimensional energy spectra undergo steepening from the Kolmogorov 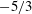$-5/3$ to the 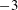$-3$ slope.

JFM classification

Geophysical and Geological Flows: Rotating flows Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 805 , 25 October 2016 , pp. 384 - 421
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baerenzung, J., Mininni, P. D., Pouquet, A., Politano, H. & Ponty, Y. 2010 Spectral modeling of rotating turbulent flows. Phys. Fluids 22, 025104.Google Scholar
Baerenzung, J., Politano, H., Ponty, Y. & Pouquet, A. 2008 Spectral modeling of turbulent flows and the role of helicity. Phys. Rev. E 77, 046303.Google Scholar
Bardina, J., Ferziger, J. H. & Rogallo, R. S. 1985 Effect of rotation on isotropic turbulence: computation and modeling. J. Fluid Mech. 154, 321–1985.Google Scholar
Bartello, P. 1995 Geostrophic adjustment and inverse cascades in rotating stratified turbulence. J. Atmos. Sci. 52, 4410–4428.Google Scholar
Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 414, 43–164.Google Scholar
Bourouiba, L. & Bartello, P. 2007 The intermediate Rossby number range and two-dimensional transfers in rotating decaying homogeneous turbulence. J. Fluid Mech. 587, 139–161.Google Scholar
Bourouiba, L., Straub, D. N. & Waite, M. L. 2012 Non-local energy transfers in rotating turbulence at intermediate Rossby number. J. Fluid Mech. 690, 129–147.Google Scholar
Bradshaw, P. 1973 Effects of streamline curvature on turbulent flow. AGARDograph 169.Google Scholar
Cambon, C. 2001 Turbulence and vortex structures in rotating and stratified flows. Eur. J. Mech. (B/Fluids) 20, 489–510.Google Scholar
Cambon, C., Godeferd, F. S., Nicolleau, F. C. G. A. & Vassilicos, J. C. 2004 Turbulent diffusion in rapidly rotating flows with and without stable stratification. J. Fluid Mech. 499, 231–255.CrossRefGoogle Scholar
Cambon, C. & Jacquin, L. 1989 Spectral approach to non-isotropic turbulence subjected to rotation. J. Fluid Mech. 202, 295–317.Google Scholar
Cambon, C., Mansour, N. N. & Godeferd, F. S. 1997 Energy transfer in rotating turbulence. J. Fluid Mech. 337, 303–332.Google Scholar
Cambon, C. & Scott, J. F. 1999 Linear and nonlinear models of anisotropic turbulence. In Annual Review of Fluid Mechanics, vol. 31, pp. 1–53. Annual Reviews.Google Scholar
Canuto, V. M. & Dubovikov, M. S. 1996 Dynamical model for turbulence: I. General formalism. Phys. Fluids 8, 571–586.Google Scholar
Canuto, V. M. & Dubovikov, M. S. 1997 A dynamical model for turbulence. V. The effect of rotation. Phys. Fluids 9, 2132–2140.Google Scholar
Charney, J. G. 1971 Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1095.Google Scholar
Chasnov, J. R. 1991 Simulation of the Kolmogorov inertial subrange using an improved subgrid model. Phys. Fluids A 3, 188–200.Google Scholar
Chekhlov, A., Orszag, S. A., Sukoriansky, S., Galperin, B. & Staroselsky, I. 1994 Direct numerical simulation tests of eddy viscosity in two dimensions. Phys. Fluids 6, 2548–2550.Google Scholar
Chen, Q., Chen, S., Eyink, G. L. & Holm, D. D. 2005 Resonant interactions in rotating homogeneous three-dimensional turbulence. J. Fluid Mech. 542, 139–164.Google Scholar
Davidson, P. A. 2013 Turbulence in Rotating, Stratified and Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Dewan, E. M. 1979 Stratospheric wave spectra resembling turbulence. Science 204, 832–835.CrossRefGoogle ScholarPubMed
Dewan, E. M. & Good, R. E. 1986 Saturation and the ‘universal’ spectrum for vertical profiles of horizontal scalar winds in the atmosphere. J. Geophys. Res. 91, 2742–2748.CrossRefGoogle Scholar
Dougherty, J. 1961 Anisotropy of turbulence at meteor level. J. Atmos. Terr. Phys. 21, 210–213.Google Scholar
Dritschel, D. G. & McKiver, W. J. 2015 Effect of Prandtl’s ratio on balance in geophysical turbulence. J. Fluid Mech. 777, 569–590.Google Scholar
Dubrulle, B. & Valdettaro, L. 1992 Consequences of rotation in energetics of accretion disks. Astron. Astrophys. 263, 387–400.Google Scholar
Fernando, H. J. S., Boyer, L. & Chen, R. 1989 Turbulent thermal convection in rotating and stratified fluids. Dyn. Atmos. Oceans 13, 95–121.Google Scholar
Fernando, H. J. S., Chen, R. & Boyer, D. L. 1991 Effects of rotation on convective turbulence. J. Fluid Mech. 228, 513–547.Google Scholar
Forster, D., Nelson, D. R. & Stephen, M. J. 1977 Large distance and long-time properties of a randomly stirred fluid. Phys. Rev. A 16, 732–749.Google Scholar
Gaite, J. 2003 Anisotropy in homogeneous rotating turbulence. Phys. Rev. E 68, 056310.Google Scholar
Galperin, B. & Sukoriansky, S. 2010 Geophysical flows with anisotropic turbulence and dispersive waves: flows with stable stratification. Ocean Dyn. 60, 427–441.Google Scholar
Galperin, B., Sukoriansky, S. & Anderson, P. S. 2007 On the critical Richardson number in stably stratified turbulence. Atmos. Sci. Let. 8, 65–69.Google Scholar
Galperin, B., Sukoriansky, S. & Dikovskaya, N. 2010 Geophysical flows with anisotropic turbulence and dispersive waves: flows with a 𝛽-effect. Ocean Dyn. 60, 427–441.Google Scholar
Galperin, B., Sukoriansky, S., Orszag, S. A. & Staroselsky, I. 1993 Non-eddy resolving model of 𝛽-plane turbulence. In Statistical methods in physical oceanography: proceedings, ‘Aha Huliko’a Hawaiian Winter Workshop, pp. 421–452. University of Hawaii at Manoa,; January 12–15.Google Scholar
Galtier, S. 2003 Weak inertial-wave turbulence theory. Phys. Rev. E 68, 015301.Google Scholar
Gibson, C. H. 1991 Laboratory, numerical, and oceanic fossil turbulence in rotating and stratified flows. J. Geophys. Res. 96, 12549–12566.Google Scholar
Gledzer, E. B. 2008 Rotation and helicity effects in cascade models of turbulence. Dokl. Phys. 53, 216–220.Google Scholar
Godeferd, F. S. & Cambon, C. 1994 Detailed investigation of energy transfers in homogeneous stratified turbulence. Phys. Fluids 6, 2084–2100.Google Scholar
Godeferd, F. S. & Moisy, F. 2015 Structure and dynamics of rotating turbulence: A review of recent experimental and numerical results. Appl. Mech. Rev. 67, 030802.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hopfinger, E. J. & Browand, F. K. 1981 Intense vortex generation by turbulence in a rotating fluid. In Proc. IUTAM-IUGG Symp. on Concentrated Atmospheric Vortices, pp. 285–297.Google Scholar
Hopfinger, E., Browand, F. & Gagne, Y. 1982 Turbulence and waves in a rotating tank. J. Fluid Mech. 125, 505–534.Google Scholar
Huang, H.-P., Galperin, B. & Sukoriansky, S. 2001 Anisotropic spectra in two-dimensional turbulence on the surface of a rotating sphere. Phys. Fluids 13, 225–240.Google Scholar
Jacquin, L., Leuchter, O., Cambon, C. & Mathieu, J. 1990 Homogeneous turbulence in the presence of rotation. J. Fluid Mech. 220, 1–52.Google Scholar
Kamenkovich, V. M., Koshlyakov, M. N. & Monin, A. S. 1986 Synoptic Eddies In The Ocean. D. Reidel Publishing Company.Google Scholar
Klein, P., Hua, B. L., Lapeyre, G., Capet, X., Gentil, S. L. & Sasaki, H. 2008 Upper ocean turbulence from high-resolution 3D simulations. J. Phys. Oceanogr. 38, 1748–1763.Google Scholar
Kraichnan, R. H. 1959 The structure of isotropic turbulence at very high Reynolds numbers. J. Fluid Mech. 5, 497–543.Google Scholar
Kraichnan, R. H. 1976 Eddy viscosity in two and three dimensions. J. Atmos. Sci. 33, 1521–1536.Google Scholar
Kraichnan, R. H. 1987 An interpretation of the Yakhot-Orszag turbulence theory. Phys. Fluids 30, 2400–2405.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1993 Fluid Mechanics, 2nd edn. Pergamon Press.Google Scholar
Lesieur, M. 1997 Turbulence in Fluids, 3rd edn. Kluwer.Google Scholar
Lindborg, E. 2005 The effect of rotation on the mesoscale energy cascade in the free atmosphere. Geophys. Res. Lett. 32, L01809, doi:10.1029/2004GL021319.Google Scholar
Lovejoy, S., Tuck, A. F., Schertzer, D. & Hovde, S. J. 2009 Reinterpreting aircraft measurements in anisotropic scaling turbulence. Atmos. Chem. Phys. 9, 5007–5025.Google Scholar
Marino, R., Mininni, P. D., Rosenberg, D. & Pouquet, A. 2013 Inverse cascades in rotating stratified turbulence: fast growth of large scales. Europhys. Lett. 102, 44006, doi:10.1209/0295-5075/102/44006.Google Scholar
Marino, R., Pouquet, A. & Rosenberg, D. 2015 Resolving the paradox of oceanic large-scale balance and small-scale mixing. Phys. Rev. Lett. 114, 114504.Google Scholar
McComb, W. D. 1991 The Physics of Fluid Turbulence. Oxford University Press.Google Scholar
Mininni, P. D. & Pouquet, A. 2010 Rotating helical turbulence. I. Global evolution and spectral behavior. Phys. Fluids 22, 035105.Google Scholar
Mininni, P. D., Rosenberg, D. & Pouquet, A. 2012 Isotropisation at small scales of rotating helically driven turbulence. J. Fluid Mech. 699, 263–279.Google Scholar
Monin, A. S. & Ozmidov, R. V. 1985 Turbulence in the Ocean. D. Reidel Publishing Company.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics. MIT Press.Google Scholar
Müller, W.-C. & Thiele, M. 2007 Scaling and energy transfer in rotating turbulence. EPL 77, 34003, doi:10.1209/0295-5075/77/34003.Google Scholar
Orszag, S. A. 1977 Statistical theory of turbulence. In Les Houches Summer School in Physics (ed. Balian, R. & Peabe, J.-L.), pp. 237–374. Gordon and Breach.Google Scholar
Ozmidov, R. V. 1965 On the turbulent exchange in a stably stratified ocean. Izv. Atmos. Ocean Phys. 1, 493–497.Google Scholar
Pedlosky, J. 1998 Ocean Circulation Theory, 2nd edn. Springer.Google Scholar
Phillips, O. M. 1977 The Dynamics of the Upper Ocean, 2nd edn. Cambridge University Press.Google Scholar
Pouquet, A. & Marino, R. 2013 Geophysical turbulence and the duality of the energy flow across scales. Phys. Rev. Lett. 111, 234501.Google Scholar
Pouquet, A., Sen, A., Rosenberg, D., Mininni, P. D. & Baerenzung, J. 2013 Inverse cascades in turbulence and the case of rotating flows. Phys. Scr. T155, 014032.Google Scholar
Read, P. L. 2011 Dynamics and circulation regimes of terrestrial planets. Planet. Space Sci. 59, 900–914.Google Scholar
Rhines, P. B. 1975 Waves and turbulence on a beta-plane. J. Fluid Mech. 69, 417–443.Google Scholar
Riley, J. J. & Lindborg, E. 2008 Stratified turbulence: a possible interpretation of some geophysical turbulence measurements. J. Atmos. Sci. 65, 2416–2424.Google Scholar
Rodriguez Imazio, P. & Mininni, P. D. 2011 Anomalous scaling of passive scalars in rotating flows. Phys. Rev. E 83, 066309.Google Scholar
Rodriguez Imazio, P. & Mininni, P. D. 2013 Effective diffusivity of passive scalars in rotating turbulence. Phys. Rev. E 87, 023018.Google Scholar
Rodriguez Imazio, P. & Mininni, P. D.2015 Passive scalars: mixing, diffusion and intermittency in helical and non-helical rotating turbulence. arXiv:1503.01345v1.Google Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.Google Scholar
Sánchez-Lavega, A. 2011 An Introduction to Planetary Atmospheres. CRC Press.Google Scholar
Schertzer, D. & Lovejoy, S. 1985 The dimension and intermittency of atmospheric dynamics. In Turbulent Shear Flow, pp. 7–33. Springer.Google Scholar
Sen, A., Mininni, P. D., Rosenberg, D. & Pouquet, A. 2012 Anisotropy and nonuniversality in scaling laws of the large-scale energy spectrum in rotating turbulence. Phys. Rev. E 86, 036319.Google Scholar
Smith, L. M., Chasnov, J. R. & Waleffe, F. 1996 Crossover from two- to three-dimensional turbulence. Phys. Rev. Lett. 77, 2467–2470.Google Scholar
Smith, L. M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11, 1608–1622.Google Scholar
Smith, L. M. & Waleffe, F. 2002 Generation of slow large scales in forced rotating stratified turbulence. J. Fluid Mech. 451, 145–168.Google Scholar
Smith, L. M. & Woodruff, S. L. 1998 Renormalization-group analysis of turbulence. In Annu. Rev. Fluid Mech., vol. 30, pp. 275–310. Annual Reviews.Google Scholar
Smith, S. A., Fritts, D. C. & Vanzandt, T. E. 1987 Evidence for saturated spectrum of atmospheric gravity waves. J. Atmos. Sci. 44, 1404–1410.Google Scholar
Sreenivasan, K. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7, 2778–2784.Google Scholar
Staplehurst, P. J., Davidson, P. A. & Dalziel, S. B. 2008 Structure formation in homogeneous, freely decaying, rotating turbulence. J. Fluid Mech. 598, 81–103.Google Scholar
Starr, V. P. 1968 Physics of Negative Viscosity Phenomena. McGraw-Hill.Google Scholar
Sukoriansky, S., Chekhlov, A., Orszag, S. A., Galperin, B. & Staroselsky, I. 1996 Large eddy simulation of two-dimensional isotropic turbulence. J. Sci. Comput. 11, 13–45.Google Scholar
Sukoriansky, S. & Galperin, B. 2013 An analytical theory of the buoyancy – Kolmogorov subrange transition in turbulent flows with stable stratification. Phil. Trans. R. Soc. A 371, 20120212, doi:10.1098/rsta.2012.0212.Google Scholar
Sukoriansky, S., Galperin, B. & Chekhlov, A. 1999 Large scale drag representation in simulations of two-dimensional turbulence. Phys. Fluids 11, 3043–3053.Google Scholar
Sukoriansky, S., Galperin, B. & Staroselsky, I. 2003 Cross-terms and 𝜖-expansion in RNG theory of turbulence. Fluid Dyn. Res. 33, 319–331.Google Scholar
Sukoriansky, S., Galperin, B. & Staroselsky, I. 2005 A quasinormal scale elimination model of turbulent flows with stable stratification. Phys. Fluids 17, 085107.Google Scholar
Sukoriansky, S. & Zemach, E. 2016 Theoretical study of anisotropic MHD turbulence with low magnetic Reynolds number. Phys. Scr. 91, 034001.Google Scholar
Thangam, S. & Wang, X.-H. 1999 Development of a turbulence model based on the energy spectrum for flows involving rotation. Phys. Fluids 11, 2225–2234.Google Scholar
Thiele, M. & Müller, W.-C. 2009 Structure and decay of rotating homogeneous turbulence. J. Fluid Mech. 637, 425–442.Google Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.Google Scholar
Vanyo, J. P. 1993 Rotating Fluids in Engineering and Science. Butterworth-Heinemann.Google Scholar
Woods, J. D. 1969 Report of working roup (V. Hogstrom, P. Misme, H. Ottersten and O. M. Phillips): fossil turbulence. Radio Science 4, 1365–1367.Google Scholar
Woods, J. D. 1973 Space-time characteristics of turbulence in the seasonal thermocline. Mem. Soc. Roy. Sei. VI, 109–130.Google Scholar
Woods, J. D. 1974 Diffusion due to fronts the rotation sub-range of turbulence in the seasonal thermocline. La Houille Blanche 29, 589–597.Google Scholar
Woods, J. D. 1980 Do waves limit turbulent diffusion in the ocean? Nature 288, 219–224.Google Scholar
Yakhot, V. & Orszag, S. A. 1986 Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1, 3–51.Google Scholar
Yang, X. & Domaradzki, J. A. 2004 Large eddy simulations of decaying rotating turbulence. Phys. Fluids 16, 4088–4104.Google Scholar
Yeung, P. K. & Xu, J. 2004 Effects of rotation on turbulent mixing: nonpremixed passive scalars. Phys. Fluids 16, 93–103.Google Scholar
Yeung, P. K. & Zhou, Y. 1998 Numerical study of rotating turbulence with external forcing. Phys. Fluids 10, 2895–2909.Google Scholar
Zeman, O. 1994 A note on the spectra and decay of rotating homogeneous turbulence. Phys. Fluids 6, 3221–3223.Google Scholar
Zhou, Y. 2010 Renormalization group theory for fluid and plasma turbulence. Phys. Rep. 488, 1–49.Google Scholar