Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-29T00:54:19.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Pulsating pipe flow with large-amplitude oscillations in the very high frequency regime. Part 2. Phase-averaged analysis

Published online by Cambridge University Press:  04 February 2015

M. Manna ,
A. Vacca  and
R. Verzicco
M. Manna
Affiliation:
Dipartimento di Ingegneria Industriale, Università di Napoli ‘Federico II’, via Claudio 21, 80125, Naples, Italy
A. Vacca*
Affiliation:
Dipartimento di Ingegneria Civile, Design, Edilizia e Ambiente, Seconda Università di Napoli, via Roma 29, 81031, Aversa (CE), Italy
R. Verzicco
Affiliation:
Dipartimento di Ingegneria Industriale, Università di Roma ‘Tor Vergata’, via del Politecnico 1, 00133, Roma, Italy PoF and MESA+, University of Twente, Drienerlolaan 5, 7522 NB, Enschede, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is the follow-up of a previous study (Manna, Vacca & Verzicco, J. Fluid Mech., vol. 700, 2012, pp. 246–282) that numerically investigated the effects of a harmonic volume forcing on the turbulent pipe flow at a bulk Reynolds number of 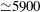$\simeq 5900$ . There, the investigation was focused on the time- and space-averaged statistics of the first- and second-order moments of the velocity, the vorticity fluctuations and the Reynolds stress budgets in order to study the changes induced on the mean current by the oscillating component. The amplitude of the latter was used as a parameter for the analysis. However, as the flow is inherently unsteady, the phase-averaged statistics are also of interest, and this is the motivation and subject of the present study. Here, we show the variability of the above quantities during different phases of the flow cycle and how they are affected by the amplitude of the oscillation. It is observed that when the ratio of the oscillating to the time-constant velocity component is of the order of one ( 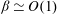${\it\beta}\simeq O(1)$ ), the phase-averaged profiles are appreciably influenced by the pulsation, although only small deviations of the time-averaged counterparts have been documented. 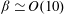In contrast, when that ratio is increased by one order of magnitude ( ${\it\beta}\simeq O(10)$ ) the phase- and cycle-averaged quantities differ considerably, especially during the decelerating part of the cycle. In more detail, the amplitude and the phase of all turbulence statistics show significant variations with 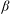${\it\beta}$ . This variability has important implications in the dynamics and modelling of these flows. Since the data have been obtained by direct numerical simulations and validated by comparisons with experimental studies, the results could be used for validation of codes, testing of turbulence models or measurement procedures.

JFM classification

Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 766 , 10 March 2015 , pp. 272 - 296
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhavan, R., Kamm, R. D. & Shapiro, A. H. 1991 An investigation of transition to turbulence in bounded oscillatory Stokes flows. Part 1. Experiments. J. Fluid Mech. 225, 395–442.CrossRefGoogle Scholar
Caro, C. G., Pedley, T. J., Schroter, R. C. & Seed, W. A. 1978 The Mechanics of the Circulation. Oxford University Press.Google Scholar
Chin, C., Ooi, S. H., Marusic, I. & Blackburn, H. M. 2010 The influence of pipe length on turbulence statistics computed from direct numerical simulation data. Phys. Fluids 22, 115107.CrossRefGoogle Scholar
Eggels, J. G. M., Unger, F., Weiss, M. H., Westerweel, J., Adrian, R. J., Friedrich, R. & Nieuwstadt, F. T. M. 1994 Fully developed turbulent pipe flow: a comparison between direct numerical simulation and experiment. J. Fluid Mech. 268, 175–210.CrossRefGoogle Scholar
He, S. & Jackson, J. D. 2009 An experimental study of pulsating turbulent flow in a pipe. Eur. J. Mech. (B/Fluids) 28, 309–320.CrossRefGoogle Scholar
Hinze, J. O. 1975 Turbulence. McGraw Hill.Google Scholar
Lodahl, C. R., Sumer, B. M. & Fredosoe, J. 1998 Turbulent combined oscillatory flow and current in a pipe. J. Fluid Mech. 373, 313–348.CrossRefGoogle Scholar
Manna, M. & Vacca, A. 1999 An efficient method for the solution of the incompressible Navier–Stokes equations in cylindrical geometries. J. Comput. Phys. 151, 563–584.CrossRefGoogle Scholar
Manna, M. & Vacca, A. 2005 Resistance reduction in pulsating turbulent pipe flow. Trans. ASME J. Engng Gas Turbines Power 127, 410–417.CrossRefGoogle Scholar
Manna, M. & Vacca, A. 2007 Spectral dynamic of pulsating turbulent pipe flow. Comput. Fluids 37, 825–835.CrossRefGoogle Scholar
Manna, M. & Vacca, A. 2009 Torque reduction in Taylor–Couette flows subject to an axial pressure gradient. J. Fluid Mech. 639, 373–401.CrossRefGoogle Scholar
Manna, M., Vacca, A. & Deville, M. 2004 Preconditioned spectral multi-domain discretization of the incompressible Navier–Stokes equations. J. Comput. Phys. 201, 204–223.CrossRefGoogle Scholar
Manna, M., Vacca, A. & Verzicco, R. 2012 Pulsating pipe fow with large-amplitude oscillations in the very high frequency regime. Part 1. Time-averaged analysis. J. Fluid Mech. 700, 246–282.CrossRefGoogle Scholar
Moin, P. & Kim, J. 1981 Numerical investigation of turbulent channel flow. J. Fluid Mech. 118, 341–377.CrossRefGoogle Scholar
Orlandi, P. & Fatica, M. 1997 Direct simulations of a turbulent pipe rotating along the axis. J. Fluid Mech. 343, 43–72.CrossRefGoogle Scholar
Quadrio, M. & Sibilla, S. 2000 Numerical simulation of turbulent flow in a pipe oscillating around its axis. J. Fluid Mech. 424, 217–241.CrossRefGoogle Scholar
Scotti, A. & Piomelli, U. 2001 Numerical simulation of pulsating turbulent channel flow. Phys. Fluids 13 (5), 1367–1384.CrossRefGoogle Scholar
Shemer, L. & Kit, E. 1984 An experimental investigation of the quasisteady turbulent pulsating flow in a pipe. Phys. Fluids 27, 72–76.CrossRefGoogle Scholar
Skote, M. 2013 Comparison between spatial and temporal wall oscillations in turbulent boundary layer flows. J. Fluid Mech. 730, 273–294.CrossRefGoogle Scholar
Tardu, S. F. & Binder, G. 1993 Wall shear stress modulation in unsteady turbulent channel flow with high imposed frequencies. Phys. Fluids 5, 2028–2034.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Touber, E. & Leschziner, M. A. 2012 Near-wall streak modification by spanwise oscillatory wall motion and drag-reduction mechanisms. J. Fluid Mech. 693, 150–200.CrossRefGoogle Scholar
Tsinober, A. 2001 An Informal Introduction to Turbulence. Kluwer Academic.CrossRefGoogle Scholar
de Tullio, M. D., Cristallo, A., Balaras, E. & Verzicco, R. 2009 Direct numerical simulation of the pulsatile flow through an aortic bileaflet mechanical heart valve. J. Fluid Mech. 622, 259–290.CrossRefGoogle Scholar
Yellin, E. L. 1966 Laminar turbulent transition process in pulsatile flow. Circulat. Res. 19, 791–804.CrossRefGoogle ScholarPubMed