Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T03:31:59.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Pulsating pipe flow with large-amplitude oscillations in the very high frequency regime. Part 1. Time-averaged analysis

Published online by Cambridge University Press:  25 April 2012

M. Manna ,
A. Vacca  and
R. Verzicco
M. Manna
Affiliation:
Dipartimento di Ingegneria Meccanica per l’Energetica, Università di Napoli ‘Federico II’, via Claudio 21, 80125 Naples, Italy
A. Vacca
Affiliation:
Dipartimento di Ingegneria Civile, Seconda Università di Napoli, via Roma 29, 81031 Aversa (CE), Italy
R. Verzicco*
Affiliation:
Dipartimento di Ingegneria Meccanica, Università di Roma ‘Tor Vergata’, via del Politecnico 1, 00133 Rome, Italy Physics of Fluids Group, University of Twente, Drienerlolaan 5, 7522 NB Enschede, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper numerically investigates the effects of a harmonic volume forcing of prescribed frequency on the turbulent pipe flow at a Reynolds number, based on bulk velocity and pipe diameter, of 5900. The thickness of the Stokes layer, resulting from the oscillatory flow component, is a small fraction of the pipe radius and therefore the associated vorticity is confined within a few wall units. 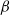The harmonic forcing term is prescribed so that the ratio of the oscillating to the mean bulk velocity () ranges between 1 and 10.6. In all cases the oscillatory flow obeys the Stokes analytical velocity distribution while remarkable changes in the current component are observed. At intermediate values 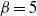, a relaminarization process occurs, while for 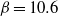, turbulence is affected so much by the harmonic forcing that the near-wall coherent structures, although not fully suppressed, are substantially weakened. The present study focuses on the analysis of the time- and space-averaged statistics of the first- and second-order moments, vorticity fluctuations and Reynolds stress budgets. Since the flow is unsteady not only locally but also in its space-averaged dynamics, it can be analysed using phase-averaged and time-averaged statistics. While the former gives information about the statistics of the fluctuations about the mean, the latter, postponed to a subsequent paper, shows how the mean is affected by the fluctuations. Clearly, the two phenomena are connected and both of them deserve investigation.

JFM classification

Boundary Layers: Pipe flow boundary layer
Type
Papers
Information
Journal of Fluid Mechanics , Volume 700 , 10 June 2012 , pp. 246 - 282
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions. Dover.Google Scholar
2. Akhavan, R., Kamm, R. D. & Shapiro, A. H. 1991 An investigation of transition to turbulence in bounded oscillatory Stokes flows. Part 1. Experiments. J. Fluid Mech. 225, 395–442.CrossRefGoogle Scholar
3. Barenblatt, G. I. 1993a Scaling laws for fully developed shear flows. Part 1. Basic hypotheses and analysis. J. Fluid Mech. 248, 513–520.CrossRefGoogle Scholar
4. Barenblatt, G. I. 1993b Scaling laws for fully developed shear flows. Part 2. Processing of experimental data. J. Fluid Mech. 248, 521–529.CrossRefGoogle Scholar
5. Bhaganagar, K. 2008 Direct numerical simulation of unsteady flow in channel with rough walls. Phys. Fluids 20, 101508.Google Scholar
6. Binder, G. & Kueny, J. L. 1981 Measurements of the periodic velocity oscillations near the wall in unsteady turbulent channel flow. In Unsteady Turbulent Shear Flow (ed. Michel, R., Cousteix, J. & Houdeville, R ), pp. 100–109. Springer.Google Scholar
7. Binder, G., Tardu, S. F. & Vezin, P. 1995 Cyclic modulation of Reynolds stresses and length scales in pulsed turbulent channel flow. Proc. R. Soc. Lond. A 451 (1941), 121–139.Google Scholar
8. Blackwelder, R. F. & Haritonidis, J. H. 1983 Scaling of the bursting frequency in turbulent boundary layers. J. Fluid Mech. 132, 87–103.CrossRefGoogle Scholar
9. Blel, W., Le Gentil-Lelievreb, C., Bénézechb, T. & Legentilhomme, P. 2009 Application of turbulent pulsating flows to the bacterial removal during a cleaning in place procedure. Part 1. Experimental analysis of wall shear stress in a cylindrical pipe. J. Food Engng 90 (4), 422–432.Google Scholar
10. Brereton, G. J., Reynolds, W. C. & Jayaraman, R. 1990 Response of a turbulent boundary layer to sinusoidal free stream unsteadiness. J. Fluid Mech. 221, 131–159.Google Scholar
11. Choi, K. S. 1989 Near-wall structure of a turbulent boundary layer with riblets. J. Fluid Mech. 208, 417–459.CrossRefGoogle Scholar
12. Eggels, J. G. M., Unger, F., Weiss, M. H., Westerweel, J., Adrian, R. J., Friedrich, R. & Nieuwstadt, F. T. M. 1994 Fully developed turbulent pipe flow: a comparison between direct numerical simulation and experiment. J. Fluid Mech. 268, 175–210.Google Scholar
13. Fedele, F., Hitt, D. L. & Prabhub, R. D. 2005 Revisiting the stability of pulsatile pipe flow. Eur. J. Mech. (B/Fluids) 24, 237–254.Google Scholar
14. Frohnapfel, B., Lammers, P., Jovanović, J. & Durst, F. 2007 Interpretation of the mechanism associated with turbulent drag reduction in terms of anisotropy invariants. J. Fluid Mech. 577, 457–466.CrossRefGoogle Scholar
15. Gilbrech, D. A. & Coombs, G. D. 1963 Critical Reynolds numbers for incompressible pulsating flow in tubes. Dev. Theor. Appl. Mech. 1, 292–304.Google Scholar
16. Grosch, C. E. & Salwen, H. 1968 The stability of steady and time-dependent plane Poiseuille flow. J. Fluid Mech. 34 (1), 177–205.CrossRefGoogle Scholar
17. Hall, P. 1975 The stability of Poiseuille flow modulated at high frequencies. Proc. R. Soc. Lond. A 344 (1639), 453–464.Google Scholar
18. He, S. & Jackson, J. D. 2009 An experimental study of pulsating turbulent flow in a pipe. Eur. J. Mech. (B/Fluids) 28, 309–320.CrossRefGoogle Scholar
19. Herbert, D. M. 1972 The energy balance in modulated plane Poiseuille flow. J. Fluid Mech. 56 (1), 73–80.Google Scholar
20. Hinze, J. O. 1975 Turbulence. McGraw-Hill.Google Scholar
21. Hwang, J.-L. & Brereton, G. J. 1991 Turbulence in high-frequency periodic fully-developed pipe flow. In Eighth International Symposium on Turbulent Shear Flows (ed. Durst, F., Friedrich, R., Launder, B. E., Schmidt, F. W., Schuman, U. & Whitelaw, J. H. ). Springer.Google Scholar
22. von Kerczek, C. H. 1982 The instability of oscillatory plane Poiseuille flow. J. Fluid Mech. 116, 91–114.CrossRefGoogle Scholar
23. Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
24. Lee, M. & Reynolds, W. 1985 Numerical experiments on the structure of homogeneous turbulence. Tech. Rep. TF-24. Thermoscience Division, Stanford University.CrossRefGoogle Scholar
25. Lodahl, C. R., Sumer, B. M. & Fredosoe, J. 1998 Turbulent combined oscillatory flow and current in a pipe. J. Fluid Mech. 373, 313–348.CrossRefGoogle Scholar
26. Luchik, T. S. & Tiederman, W. G. 1987 Timescale and structure of ejections and burst in turbulent channel flow. J. Fluid Mech. 174, 529–552.CrossRefGoogle Scholar
27. Lumley, J. L. & Newman, G. 1977 The return to isotropy of homogeneous turbulence. J. Fluid Mech. 82, 161–178.CrossRefGoogle Scholar
28. Manna, M. & Vacca, A. 1999 An efficient method for the solution of the incompressible Navier–Stokes equations in cylindrical geometries. J. Comput. Phys. 151, 563–584.CrossRefGoogle Scholar
29. Manna, M. & Vacca, A. 2005 Resistance reduction in pulsating turbulent pipe flow. Trans. ASME: J. Engng Gas Turbines Power 127, 410–417.Google Scholar
30. Manna, M. & Vacca, A. 2007 Spectral dynamic of pulsating turbulent pipe flow. Comput. Fluids 37, 825–835.CrossRefGoogle Scholar
31. Manna, M. & Vacca, A. 2009 Torque reduction in Taylor–Couette flows subject to an axial pressure gradient. J. Fluid Mech. 639, 373–401.Google Scholar
32. Mao, Z. X. & Hanratty, T. J. 1986 Studies of the wall shear stress in a turbulent pulsating pipe flow. J. Fluid Mech. 170, 545–564.CrossRefGoogle Scholar
33. Mao, Z. X. & Hanratty, T. J. 1994 Influence of large-amplitude oscillations on turbulent drag. AIChE J. 40 (10), 1601–1610.Google Scholar
34. Mizuchina, T., Maruyama, T & Shiozaki, Y. 1973 Pulsating turbulent flow in a tube. J. Chem. Engng Japan 6, 487–495.Google Scholar
35. Mizushina, T., Maruyama, T. & Hirasawa, H. 1975 Structure of the turbulence in pulsating pipe flows. J. Chem. Engng Japan 8, 210–216.CrossRefGoogle Scholar
36. Moin, P. & Kim, J. 1981 Numerical investigation of turbulent channel flow. J. Fluid Mech. 118, 341–377.Google Scholar
37. Moser, R., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to . Phys. Fluids 177, 133–166.Google Scholar
38. Moser, R. D. & Moin, P. 1984 Direct numerical simulation of curved channel flow. TM 85974. NASA.Google Scholar
39. Orlandi, P. & Ebstein, D. 2000 Turbulent budgets in rotating pipes by DNS. Intl J. Heat Fluid Flow 21, 499–505.Google Scholar
40. Orlandi, P. & Fatica, M. 1997 Direct simulations of a turbulent pipe rotating along the axis. J. Fluid Mech. 343, 43–72.Google Scholar
41. Oyewola, O., Djenidi, L. & Antonia, R. A. 2004 Influence of localised wall suction on the anisotropy of the Reynolds stress tensor in a turbulent boundary layer. Exp. Fluids 37, 187–193.Google Scholar
42. Ptasinski, P. K., Boersma, B. J., Nieuwstadt, F. T. M., Hulsen, M. A., Van Den Brule, B. H. A. A. & Hunt, J. C. R. 2003 Turbulent channel flow near maximum drag reduction: simulations, experiments and mechanisms. J. Fluid Mech. 490, 251–291.CrossRefGoogle Scholar
43. Quadrio, M., Ricco, P. & Viotti, C. 2009 Streamwise travelling waves of spanwise wall velocity for turbulent drag reduction. J. Fluid Mech. 627, 161–178.CrossRefGoogle Scholar
44. Quadrio, M. & Sibilla, S. 2000 Numerical simulation of turbulent flow in a pipe oscillating around its axis. J. Fluid Mech. 424, 217–241.Google Scholar
45. Ramaprian, B. R. & Tu, S. W. 1980 An experimental study of oscillatory pipe flow at transitional Reynolds number. J. Fluid Mech. 100, 513–544.CrossRefGoogle Scholar
46. Ramaprian, B. R. & Tu, S. W. 1983 Fully developed periodic turbulent pipe flow. Part 2. The detailed structure of the flow. J. Fluid Mech. 137, 59–81.Google Scholar
47. Reynolds, W. C. & Kassinos, S. C. 1995 One-point modelling of rapidly deformed homogeneous turbulence. Proc. R. Soc. Lond. A 451, 87–104.Google Scholar
48. Ronneberger, D. & Ahrens, C. D. 1977 Wall shear stress caused by signal amplitude perturbations of turbulent boundary-layer flow: an experimental investigation. J. Fluid Mech. 83, 433–464.Google Scholar
49. Sarpkaja, T. 1966 Experimental determination of the critical Reynolds number for pulsating Poiseuille flow. Trans. ASME: J. Basic Engng 88, 589–598.CrossRefGoogle Scholar
50. Scotti, A. & Piomelli, U. 2001 Numerical simulation of pulsating turbulent channel flow. Phys. Fluids 13 (5), 1367–1384.CrossRefGoogle Scholar
51. Shemer, L. 1985 Laminar–turbulent transition in a slowly pulsating pipe flow. Phys. Fluids 28, 3506–3509.Google Scholar
52. Shemer, L. & Kit, E. 1984 An experimental investigation of the quasisteady turbulent pulsating flow in a pipe. Phys. Fluids 27, 72–76.CrossRefGoogle Scholar
53. Shemer, L., Wygnanski, I. & Kit, E. 1985 Pulsating flow in a pipe. J. Fluid Mech. 153, 313–337.Google Scholar
54. Singer, B., Ferziger, J. H. & Reed, H. 1989 Numerical simulation of transition in oscillatory plane channel flow. J. Fluid Mech. 208, 44–66.Google Scholar
55. Stettler, J. C. & Hussain, A. K. M. F. 1986 On transition of the pulsatile flow. J. Fluid Mech. 170, 169–197.CrossRefGoogle Scholar
56. Tardu, S. F. & Binder, G. 1993 Wall shear stress modulation in unsteady turbulent channel flow with high imposed frequencies. Phys. Fluids 5, 2028–2034.Google Scholar
57. Tardu, S. F., Binder, G. & Blackwelder, R. F. 1994 Turbulent channel flow with large-amplitude velocity oscillations. J. Fluid Mech. 267, 109–151.CrossRefGoogle Scholar
58. Tozzi, J. T. & von Kerczek, C. H. 1986 The stability of oscillatory Hagen–Poiseuille flow. Trans. ASME: J. Appl. Mech. 53, 187–192.Google Scholar
59. Tu, S. W. & Ramaprian, B. R. 1983 Fully developed periodic turbulent pipe flow. Part 1. Main experimental results and comparison with predictions. J. Fluid Mech. 137, 31–58.CrossRefGoogle Scholar
60. Tuzi, R. & Blondeaux, P. 2008 Intermittent turbulence in a pulsating pipe flow. J. Fluid Mech. 599, 51–79.Google Scholar
61. Van Kan, J. 1986 A second-order accurate pressure correction scheme for viscous incompressible flow. J. Sci. Stat. Comput. 7, 870–891.CrossRefGoogle Scholar
62. Viotti, C., Quadrio, M. & Luchini, P. 2009 Streamwise oscillation of spanwise velocity at the wall for turbulent drag reduction. Phys. Fluid 21, 115109.CrossRefGoogle Scholar
63. Wallace, J. M., Ecklmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54, 39–48.Google Scholar
64. Willmarth, W. W. & Lu, S. S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55, 65–92.Google Scholar
65. Yellin, E. L. 1966 Laminar–turbulent transition process in pulsatile flow. Circulat. Res. 19, 791–804.CrossRefGoogle ScholarPubMed
66. Zagarola, M. V. & Smits, A. J. 1998 Mean flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.Google Scholar
67. Zou, L. Y., Liu, N. S. & Lu, X. Y. 2006 An investigation of pulsating turbulent open channel flow by large eddy simulation. Comput. Fluids 35 (1), 74–102.Google Scholar