Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-19T22:54:36.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Properties of the mean momentum balance in turbulent Taylor–Couette flow

Published online by Cambridge University Press:  20 March 2020

Tie Wei Open the ORCID record for Tie Wei [Opens in a new window]
Tie Wei*
Affiliation:
Department of Mechanical Engineering, New Mexico Institute of Mining and Technology, Socorro, NM 87801, USA
*
† Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates the properties of the mean momentum balance (MMB) equation in the azimuthal $\unicode[STIX]{x1D719}$ direction of a turbulent Taylor–Couette flow (TCF). The MMB-$\unicode[STIX]{x1D719}$ equation is integrated to determine the properties of the Reynolds shear stress. An approximation is developed for the Reynolds shear stress in the core region of a turbulent TCF, and the dependence of the peak Reynolds shear stress location on the Reynolds number and the gap geometry is revealed. The properties of the global integral of the turbulent Coriolis force are also revealed. For a turbulent TCF with a small gap or at high Reynolds numbers, the global integral of the turbulent Coriolis force is found to be only weakly influenced by the rotation ratio of the cylinders. Two controlling non-dimensional numbers are derived directly from the scaling analysis of the MMB-$\unicode[STIX]{x1D719}$ equation. The first is a geometry Atwood number $A_{t}\stackrel{\text{def}}{=}\unicode[STIX]{x1D6FF}/r_{ctr}$ to characterize the gap geometry, where $\unicode[STIX]{x1D6FF}$ is the gap half-width, and $r_{ctr}$ is the mid-gap radial location. 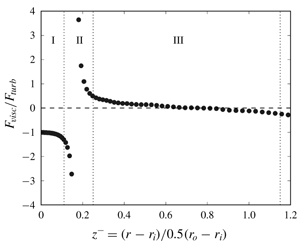The second is the friction Reynolds number $Re_{\unicode[STIX]{x1D70F},i}$ defined as $Re_{\unicode[STIX]{x1D70F},i}\stackrel{\text{def}}{=}\unicode[STIX]{x1D6FF}u_{\unicode[STIX]{x1D70F},i}/\unicode[STIX]{x1D708}$, where $\unicode[STIX]{x1D708}$ is the kinematic viscosity and $u_{\unicode[STIX]{x1D70F},i}$ is the friction velocity at the inner cylinder. A new three-layer structure is proposed for the inner half of a turbulent TCF at sufficiently high Reynolds number, based on the force balance in the MMB-$\unicode[STIX]{x1D719}$ equation. Layer I is an inner layer, where the force balance is between the viscous force and the Reynolds shear force: $F_{visc}\approx -F_{turb}$. Layer III occupies the core of the gap, where the force balance is between the turbulent Coriolis force and the Reynolds shear force: $F_{cori}\approx -F_{turb}$. In Layer II, all three forces contribute to the balance. An inner scaling is developed for Layer I, and an outer scaling is developed for Layer III. The inner and outer scalings are verified against direct numerical simulation data. Similarities and differences between the turbulent TCF and a pressure-driven turbulent channel flow are elucidated.

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 891 , 25 May 2020 , A10
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Matsuo, Y. 2001 Direct numerical simulation of a fully developed turbulent channel flow with respect to the Reynolds number dependence. Trans. ASME J. Fluids Engng 123 (2), 382–393.CrossRefGoogle Scholar
Afzal, N. 1982 Fully developed turbulent flow in a pipe: an intermediate layer. Arch. Appl. Mech. 52 (6), 355–377.Google Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
Brauckmann, H. J. & Eckhardt, B. 2013 Direct numerical simulations of local and global torque in Taylor–Couette flow up to Re = 30 000. J. Fluid Mech. 718, 398–427.CrossRefGoogle Scholar
Chouippe, A., Climent, E., Legendre, D. & Gabillet, C. 2014 Numerical simulation of bubble dispersion in turbulent Taylor–Couette flow. Phys. Fluids 26 (4), 043304.CrossRefGoogle Scholar
Couette, M. 1890 Études sur le frottement des liquides. Ann. Chim. Phys. 21, 433.Google Scholar
Dong, S. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 587, 373–393.CrossRefGoogle Scholar
Dong, S. 2008 Turbulent flow between counter-rotating concentric cylinders: a direct numerical simulation study. J. Fluid Mech. 615, 371–399.CrossRefGoogle Scholar
Donnelly, R. J. 1991 Taylor–Couette flow: the early days. Phys. Today 44 (11), 32–39.CrossRefGoogle Scholar
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P.-Y., Richard, D. & Zahn, J.-P. 2005 Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17 (9), 095103.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.CrossRefGoogle Scholar
Fardin, M. A., Perge, C. & Taberlet, N. 2014 ‘The hydrogen atom of fluid dynamics’ – introduction to the Taylor–Couette flow for soft matter scientists. Soft Matt. 10 (20), 3523–3535.CrossRefGoogle Scholar
Fife, P.2006 Scaling approaches to steady wall-induced turbulence. http://www.math.utah.edu/∼fife/revarticle.pdf.Google Scholar
Fife, P., Klewicki, J., McMurtry, P. & Wei, T. 2005 Multiscaling in the presence of indeterminacy: wall-induced turbulence. Multiscale Model. Simul. 4 (3), 936–959.CrossRefGoogle Scholar
van Gils, D. P. M., Bruggert, G. W., Lathrop, D. P., Sun, C. & Lohse, D. 2011 The Twente turbulent Taylor–Couette (T3C) facility: strongly turbulent (multiphase) flow between two independently rotating cylinders. Rev. Sci. Instrum. 82 (2), 025105.CrossRefGoogle ScholarPubMed
Glimm, J., Grove, J. W., Li, X. L., Oh, W. & Sharp, D. H. 2001 A critical analysis of Rayleigh–Taylor growth rates. J. Comput. Phys. 169 (2), 652–677.CrossRefGoogle Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High–Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48, 53–80.CrossRefGoogle Scholar
Huisman, S. G., Van D Veen, R. C., Sun, C. & Lohse, D. 2014 Multiple states in highly turbulent Taylor–Couette flow. Nat. Commun. 5, 3820.CrossRefGoogle ScholarPubMed
Kawamura, H., Abe, H. & Shingai, K. 2000 DNS of turbulence and heat transport in a channel flow with different Reynolds and Prandtl numbers and boundary conditions. Turbulence, Heat and Mass Transfer 3, 15–32.Google Scholar
Klewicki, J., Fife, P., Wei, T. & McMurtry, P. 2007 A physical model of the turbulent boundary layer consonant with mean momentum balance structure. Phil. Trans. R. Soc. Lond. A 365 (1852), 823–840.CrossRefGoogle ScholarPubMed
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics. Pergamon Press.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 5200. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Livescu, D., Ristorcelli, J. R., Gore, R. A., Dean, S. H., Cabot, W. H. & Cook, A. W. 2009 High-Reynolds number Rayleigh–Taylor turbulence. J. Turbul. 10, N13.CrossRefGoogle Scholar
Long, R. R. & Chen, T.-C. 1981 Experimental evidence for the existence of the ‘mesolayer’ in turbulent systems. J. Fluid Mech. 105, 19–59.CrossRefGoogle Scholar
Mallock, A. 1896 Experiments on fluid viscosity. Phil. Trans. R. Soc. Lond. A 187, 41–56.Google Scholar
Martínez-Arias, B., Peixinho, J., Crumeyrolle, O. & Mutabazi, I. 2014 Effect of the number of vortices on the torque scaling in Taylor–Couette flow. J. Fluid Mech. 748, 756–767.CrossRefGoogle Scholar
Merbold, S., Brauckmann, H. J. & Egbers, C. 2013 Torque measurements and numerical determination in differentially rotating wide gap Taylor–Couette flow. Phys. Rev. E 87 (2), 023014.Google ScholarPubMed
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.CrossRefGoogle Scholar
Ostilla-Mónico, R., Huisman, S. G., Jannink, T. J. G., Van Gils, D. P. M., Verzicco, R., Grossmann, S., Sun, C. & Lohse, D. 2014 Optimal Taylor–Couette flow: radius ratio dependence. J. Fluid Mech. 747, 1–29.CrossRefGoogle Scholar
Ostilla-Mónico, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.CrossRefGoogle Scholar
Ostilla-Mónico, R., Verzicco, R. & Lohse, D. 2015 Effects of the computational domain size on direct numerical simulations of Taylor–Couette turbulence with stationary outer cylinder. Phys. Fluids 27 (2), 025110.CrossRefGoogle Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2016 Passive scalars in turbulent channel flow at high Reynolds number. J. Fluid Mech. 788, 614–639.CrossRefGoogle Scholar
Pirro, D. & Quadrio, M. 2008 Direct numerical simulation of turbulent Taylor–Couette flow. Eur. J. Mech. (B/Fluids) 27 (5), 552–566.CrossRefGoogle Scholar
Pope, S. B. 2001 Turbulent Flows. Cambridge University Press.Google Scholar
Ravelet, F., Delfos, R. & Westerweel, J. 2010 Influence of global rotation and Reynolds number on the large-scale features of a turbulent Taylor–Couette flow. Phys. Fluids 22 (5), 055103.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2016 Boundary-Layer Theory. Springer.Google Scholar
Shingai, K., Kawamura, H. & Matsuo, Y. 2000 DNS of turbulent Couette flow and its comparison with turbulent Poiseuille flow. In Advances in Turbulence 8 (Proceedings of the 8th European Turbulence Conference (ed. Dopazo, C. et al. ), p. 972. CIMNE.Google Scholar
Sreenivasan, K. R. & Sahay, A.1997 The persistence of viscous effects in the overlap region and the mean velocity in turbulent pipe and channel flows. arXiv:physics/9708016.Google Scholar
Tanaka, R., Kawata, T. & Tsukahara, T. 2018 DNS of Taylor–Couette flow between counter-rotating cylinders at small radius ratio. Int. J. Adv. Eng. Sci. Appl. Math 10 (2), 159–170.CrossRefGoogle Scholar
Taylor, G. I. 1936 Fluid friction between rotating cylinders iidistribution of velocity between concentric cylinders when outer one is rotating and inner one is at rest. Phil. Trans. R. Soc. Lond. A 157 (892), 565–578.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Townsend, A. A. R. 1980 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Tsukahara, T., Kawamura, H. & Shingai, K. 2006 DNS of turbulent Couette flow with emphasis on the large-scale structure in the core region. J. Turbul. 7, N19.CrossRefGoogle Scholar
Van Gils, D. P. M., Huisman, S. G., Grossmann, S., Sun, C. & Lohse, D. 2012 Optimal Taylor–Couette turbulence. J. Fluid Mech. 706, 118–149.CrossRefGoogle Scholar
Wei, T. 2018 Multiscaling analysis of the mean thermal energy balance equation in fully developed turbulent channel flow. Phys. Rev. F 3 (9), 094608.Google Scholar
Wei, T. 2019 Multiscaling analysis of buoyancy-driven turbulence in a differentially heated vertical channel. Phys. Rev. F 4, 073502.Google Scholar
Wei, T., Fife, P., Klewicki, J. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.CrossRefGoogle Scholar
Wei, T. & Livescu, D. 2012 Late-time quadratic growth in single-mode Rayleigh–Taylor instability. Phys. Rev. E 86 (4), 046405.Google ScholarPubMed
Zimmerman, D. S., Triana, S. A. & Lathrop, D. P. 2011 Bi-stability in turbulent, rotating spherical Couette flow. Phys. Fluids 23 (6), 065104.CrossRefGoogle Scholar