Article contents
Prograde, retrograde, and oscillatory modes in rotating Rayleigh–Bénard convection
Published online by Cambridge University Press: 13 October 2017
Abstract
Rotating Rayleigh–Bénard convection is typified by a variety of regimes with very distinct flow morphologies that originate from several instability mechanisms. Here we present results from direct numerical simulations of three representative set-ups: first, a fluid with Prandtl number  $Pr=6.4$, corresponding to water, in a cylinder with a diameter-to-height aspect ratio of
$Pr=6.4$, corresponding to water, in a cylinder with a diameter-to-height aspect ratio of 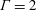 $\unicode[STIX]{x1D6E4}=2$; second, a fluid with
$\unicode[STIX]{x1D6E4}=2$; second, a fluid with 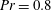 $Pr=0.8$, corresponding to
$Pr=0.8$, corresponding to 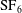 $\text{SF}_{6}$ or air, confined in a slender cylinder with
$\text{SF}_{6}$ or air, confined in a slender cylinder with 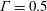 $\unicode[STIX]{x1D6E4}=0.5$; and third, the main focus of this paper, a fluid with
$\unicode[STIX]{x1D6E4}=0.5$; and third, the main focus of this paper, a fluid with 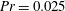 $Pr=0.025$, corresponding to a liquid metal, in a cylinder with
$Pr=0.025$, corresponding to a liquid metal, in a cylinder with 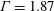 $\unicode[STIX]{x1D6E4}=1.87$. The obtained flow fields are analysed using the sparsity-promoting variant of the dynamic mode decomposition (DMD). By means of this technique, we extract the coherent structures that govern the dynamics of the flow, as well as their associated frequencies. In addition, we follow the temporal evolution of single modes and present a criterion to identify their direction of travel, i.e. whether they are precessing prograde or retrograde. We show that for moderate
$\unicode[STIX]{x1D6E4}=1.87$. The obtained flow fields are analysed using the sparsity-promoting variant of the dynamic mode decomposition (DMD). By means of this technique, we extract the coherent structures that govern the dynamics of the flow, as well as their associated frequencies. In addition, we follow the temporal evolution of single modes and present a criterion to identify their direction of travel, i.e. whether they are precessing prograde or retrograde. We show that for moderate 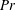 $Pr$ a few dynamic modes suffice to accurately describe the flow. For large aspect ratios, these are wall-localised waves that travel retrograde along the periphery of the cylinder. Their DMD frequencies agree with the predictions of linear stability theory. With increasing Rayleigh number
$Pr$ a few dynamic modes suffice to accurately describe the flow. For large aspect ratios, these are wall-localised waves that travel retrograde along the periphery of the cylinder. Their DMD frequencies agree with the predictions of linear stability theory. With increasing Rayleigh number 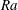 $Ra$, the interior gradually fills with columnar vortices, and eventually a regular pattern of convective Taylor columns prevails. For small aspect ratios and close enough to onset, the dominant flow structures are body modes that can precess either prograde or retrograde. For
$Ra$, the interior gradually fills with columnar vortices, and eventually a regular pattern of convective Taylor columns prevails. For small aspect ratios and close enough to onset, the dominant flow structures are body modes that can precess either prograde or retrograde. For 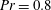 $Pr=0.8$, DMD additionally unveiled the existence of so far unobserved low-amplitude oscillatory modes. Furthermore, we elucidate the multi-modal character of oscillatory convection in low-
$Pr=0.8$, DMD additionally unveiled the existence of so far unobserved low-amplitude oscillatory modes. Furthermore, we elucidate the multi-modal character of oscillatory convection in low-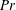 $Pr$ fluids. Generally, more dynamic modes must be retained to accurately approximate the flow. Close to onset, the flow is purely oscillatory and the DMD reveals that these high-frequency modes are a superposition of oscillatory columns and cylinder-scale inertial waves. We find that there are coexisting prograde and retrograde modes, as well as quasi-axisymmetric torsional modes. For higher
$Pr$ fluids. Generally, more dynamic modes must be retained to accurately approximate the flow. Close to onset, the flow is purely oscillatory and the DMD reveals that these high-frequency modes are a superposition of oscillatory columns and cylinder-scale inertial waves. We find that there are coexisting prograde and retrograde modes, as well as quasi-axisymmetric torsional modes. For higher 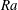 $Ra$, the flow also becomes unstable to wall modes. These low-frequency modes can both coexist with the oscillatory modes, and also couple to them. However, the typical flow feature of rotating convection at moderate
$Ra$, the flow also becomes unstable to wall modes. These low-frequency modes can both coexist with the oscillatory modes, and also couple to them. However, the typical flow feature of rotating convection at moderate 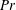 $Pr$, the quasi-steady Taylor vortices, is entirely absent in low-
$Pr$, the quasi-steady Taylor vortices, is entirely absent in low-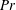 $Pr$ flows.
$Pr$ flows.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
Horn and Schmid supplementary movie 1
Supplementary movie to figure 2. DNS results showing the temperature and the azimuthal velocity for Pr = 6.4, Ra = 1.55 × 105. The movie shows 500 time units.
Horn and Schmid supplementary movie 2
Supplementary movie to figure 2. DNS results showing the temperature and the azimuthal velocity for Pr = 6.4, Ra = 6.49 × 105. The movie shows 500 time units.
Horn and Schmid supplementary movie 3
Supplementary movie to figure 2. DNS results showing the temperature and the azimuthal velocity for Pr = 6.4, Ra = 2.60 × 106. The movie shows 500 time units.
Horn and Schmid supplementary movie 4
Supplementary movie to figure 3. DNS results for Pr = 0.8 showing the temperature for Ro = 0.3 (left) and Ro = 0.5 (right). The movie shows 1000 time units.
Horn and Schmid supplementary movie 5
Supplementary movie to figure 4. Oscillatory DMD mode for Pr = 0.8 and Ro = 0.5. The movie shows the evolution over 500 time units.
Horn and Schmid supplementary movie 6
Supplementary movie to figure 8. DNS results showing the temperature and the azimuthal velocity for Pr = 0.025, Ra = 8.1 × 105, Ek = 2 × 10-5. The movie shows 50 time units.
Horn and Schmid supplementary movie 7
Supplementary movie to figure 9. DNS results showing the temperature and the azimuthal velocity for Pr = 0.025, Ra = 8.0 × 106, Ek = 5 × 10-6. The movie shows 50 time units.
Horn and Schmid supplementary movie 8
Supplementary movie to figure 12. Retrograde DMD mode for Pr = 0.025, Ra = 8.1 × 105, Ek = 2 × 10-5. The movie shows the evolution over 50 time units.
Horn and Schmid supplementary movie 9
Supplementary movie to figure 13. Prograde DMD mode for Pr = 0.025, Ra = 8.1 × 105, Ek = 2 × 10-5. The movie shows the evolution over 50 time units.
Horn and Schmid supplementary movie 10
Supplementary movie to figure 14. Axisymmetric DMD mode for Pr = 0.025, Ra = 8.1 × 105, Ek = 2 × 10-5. The movie shows the evolution over 50 time units.
Horn and Schmid supplementary movie 11
Supplementary movie to figure 15. Retrograde m = 4 DMD mode for Pr = 0.025, Ra = 8.0 × 106, Ek = 5 × 10-6. The movie shows the evolution over 50 time units.
- 45
- Cited by



