Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T22:58:18.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Pressure–strain terms in Langmuir turbulence

Published online by Cambridge University Press:  07 October 2019

Brodie C. Pearson Open the ORCID record for Brodie C. Pearson [Opens in a new window] ,
Alan L. M. Grant Open the ORCID record for Alan L. M. Grant [Opens in a new window]  and
Jeff A. Polton Open the ORCID record for Jeff A. Polton [Opens in a new window]
Brodie C. Pearson*
Affiliation:
Department of Earth, Environmental and Planetary Sciences, Brown University, Providence, RI 02912, USA College of Earth, Ocean, and Atmospheric Sciences, Oregon State University, OR 97331, USA
Alan L. M. Grant
Affiliation:
Department of Meteorology, University of Reading, Reading RG6 6UR, UK
Jeff A. Polton
Affiliation:
National Oceanography Centre, Liverpool L3 5DA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study investigates the pressure–strain tensor (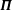$\unicode[STIX]{x1D72B}$) in Langmuir turbulence. The pressure–strain tensor is determined from large-eddy simulations (LES), and is partitioned into components associated with the mean current shear (rapid), the Stokes shear and the turbulent–turbulent (slow) interactions. The rapid component can be parameterized using existing closure models, although the coefficients in the closure models are particular to Langmuir turbulence. A closure model for the Stokes component is proposed, and it is shown to agree with results from the LES. The slow component of 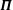$\unicode[STIX]{x1D72B}$ does not agree with existing ‘return-to-isotropy’ closure models for five of the six components of the Reynolds stress tensor, and a new closure model is proposed that accounts for these deviations which vary systematically with Langmuir number, 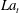$La_{t}$, and depth. The implications of these results for second- and first-order closures of Langmuir turbulence are discussed.

JFM classification

Geophysical and Geological Flows: Ocean processes Turbulent Flows: Turbulent boundary layers Waves/Free-surface Flows: Surface gravity waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 880 , 10 December 2019 , pp. 5 - 31
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andren, A. & Moeng, C. H. 1993 Single-point closures in a neutrally stratified boundary-layer. J. Atmos. Sci. 50 (20), 3366–3379.10.1175/1520-0469(1993)050<3366:SPCIAN>2.0.CO;22.0.CO;2>Google Scholar
Belcher, S. E., Grant, A. L. M., Hanley, K. E., Fox-Kemper, B., Van Roekel, L., Sullivan, P. P., Large, W. G., Brown, A., Hines, A., Calvert, D. et al. 2012 A global perspective on Langmuir turbulence in the ocean surface boundary layer. Geophys. Res. Lett. 39, L18605.Google Scholar
Bou-Zeid, E., Gao, X., Ansorge, C. & Katul, G. G. 2018 On the role of return to isotropy in wall-bounded turbulent flows with buoyancy. J. Fluid Mech. 856, 61–78.10.1017/jfm.2018.693Google Scholar
Champagne, F. H., Harris, V. G. & Corrsin, S. 1970 Experiments on nearly homogeneous turbulent shear flow. J. Fluid Mech. 41, 81–139.Google Scholar
Choi, K. S. & Lumley, J. L. 2001 The return to isotropy of homogeneous turbulence. J. Fluid Mech. 436, 59–84.10.1017/S002211200100386XGoogle Scholar
Chung, M. K. & Kim, S. K. 1995 A nonlinear return-to-isotropy model with Reynolds number and anisotropy dependency. Phys. Fluids 7 (6), 1425–1437.10.1063/1.868760Google Scholar
Craik, A. D. D. & Leibovich, S. 1976 Rational model for Langmuir circulations. J. Fluid Mech. 73, 401–426.Google Scholar
Crow, S. C. 1968 Viscoelastic properties of fine-grained incompressible turbulence. J. Fluid Mech. 33 (01), 1–20.Google Scholar
D’Alessio, S. J. D., Abdella, K. & McFarlane, N. A. 1998 A new second-order turbulence closure scheme for modeling the oceanic mixed layer. J. Phys. Oceanogr. 28 (8), 1624–1641.Google Scholar
Daly, B. J. & Harlow, F. H. 1970 Transport equations in turbulence. Phys. Fluids 13 (11), 2634–2649.Google Scholar
D’Asaro, E. A., Thomson, J., Shcherbina, A. Y., Harcourt, R. R., Cronin, M. F., Hemer, M. A. & Fox-Kemper, B. 2014 Quantifying upper ocean turbulence driven by surface waves. Geophys. Res. Lett. 41 (1), 102–107.10.1002/2013GL058193Google Scholar
D’Asaro, E. A. 2001 Turbulent vertical kinetic energy in the ocean mixed layer. J. Phys. Oceanogr. 31, 3530–3537.10.1175/1520-0485(2002)031<3530:TVKEIT>2.0.CO;22.0.CO;2>Google Scholar
Ding, M., Nguyen, K. X., Liu, S., Otte, M. J. & Tong, C. 2018 Investigation of the pressure–strain-rate correlation and pressure fluctuations in convective and near neutral atmospheric surface layers. J. Fluid Mech. 854, 88–120.Google Scholar
Gerolymos, G. A., Lo, C., Vallet, I. & Younis, B. A. 2012 Term-by-term analysis of near-wall second-moment closures. AIAA J. 50 (12), 2848–2864.10.2514/1.J051654Google Scholar
Grant, A. L. M. & Belcher, S. E. 2009 Characteristics of Langmuir turbulence in the ocean mixed layer. J. Phys. Oceanogr. 39, 1871–1887.Google Scholar
Hamlington, P. E. & Dahm, W. J. A. 2009 Nonlocal form of the rapid pressure–strain correlation in turbulent flows. Phys. Rev. E 80 (4), 046311.Google Scholar
Hamlington, P. E., Van Roekel, L. P., Fox-Kemper, B., Julien, K. & Chini, G. P. 2014 Langmuir-submesoscale interactions: descriptive analysis of multiscale frontal spin-down simulations. J. Phys. Oceanogr 117, C05001.Google Scholar
Hanjalic, K. & Launder, B. E. 1972 Reynolds stress model of turbulence and its application to thin shear flows. J. Fluid Mech. 52 (APR25), 609.10.1017/S002211207200268XGoogle Scholar
Harcourt, R. R. 2013 A second-moment closure model of Langmuir turbulence. J. Phys. Oceanogr. 43 (4), 673–697.Google Scholar
Harcourt, R. R. 2015 An improved second-moment closure model of Langmuir turbulence. J. Phys. Oceanogr. 45 (1), 84–103.10.1175/JPO-D-14-0046.1Google Scholar
Heinze, R., Mironov, D. & Raasch, S. 2016 Analysis of pressure–strain and pressure gradient-scalar covariances in cloud-topped boundary layers: a large-eddy simulation study. J. Adv. Model. Earth Sys. 8 (1), 3–30.Google Scholar
Huang, N. E. 1979 On surface drift currents in the ocean. J. Fluid Mech. 91 (01), 191–208.Google Scholar
Kantha, L. H. & Clayson, C. A. 1994 An improved mixed-layer model for geophysical applications. J. Geophys. Res. 99 (C12), 25235–25266.10.1029/94JC02257Google Scholar
Kantha, L. H. & Clayson, C. A. 2004 On the effect of surface gravity waves on mixing in the oceanic mixed layer. Ocean Model. 6 (2), 101–124.Google Scholar
Kukulka, T. & Harcourt, R. R. 2017 Influence of stokes drift decay scale on Langmuir turbulence. J. Phys. Oceanogr. 47 (7), 1637–1656.Google Scholar
Kukulka, T., Plueddemann, A. J. & Sullivan, P. P. 2013 Inhibited upper ocean restratification in nonequilibrium swell conditions. Geophys. Res. Lett. 40 (14), 3672–3676.Google Scholar
Large, W. G., McWilliams, J. C. & Doney, S. C. 1994 Oceanic vertical mixing: a review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 32 (4), 363–403.Google Scholar
Launder, B. E., Reece, G. J. & Rodi, W. 1975 Progress in development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68 (APR15), 537–566.10.1017/S0022112075001814Google Scholar
Li, Q., Webb, A., Fox-Kemper, B., Craig, A., Danabasoglu, G., Large, W. G. & Vertenstein, M. 2016 Langmuir mixing effects on global climate: WAVEWATCH III in CESM. Ocean Model. 103, 145–160.10.1016/j.ocemod.2015.07.020Google Scholar
Liu, J., Liang, J.-H., McWilliams, J. C., Sullivan, P. P., Fan, Y. & Chen, Q. 2018 Effect of planetary rotation on oceanic surface boundary layer turbulence. J. Phys. Oceanogr. 48 (9), 2057–2080.10.1175/JPO-D-17-0150.1Google Scholar
Lumley, J. L. 1975 Pressure–strain correlation. Phys. Fluids 18 (6), 750.10.1063/1.861205Google Scholar
McWilliams, J. C., Huckle, E., Liang, J. & Sullivan, P. P. 2014 Langmuir turbulence in swell. J. Phys. Oceanogr. 44, 870–890.10.1175/JPO-D-13-0122.1Google Scholar
McWilliams, J. C., Huckle, E., Liang, J.-H. & Sullivan, P. P. 2012 The wavy ekman layer: langmuir circulations, breaking waves, and Reynolds stress. J. Phys. Oceanogr. 42 (11), 1793–1816.10.1175/JPO-D-12-07.1Google Scholar
McWilliams, J. C., Sullivan, P. P. & Moeng, C. H. 1997 Langmuir turbulence in the ocean. J. Fluid Mech. 334, 1–30.10.1017/S0022112096004375Google Scholar
Mellor, G. L. & Yamada, T. 1974 A hierarchy of turbulence closure models for planetary boundary layers. J. Atmos. Sci. 31 (7), 1791–1806.Google Scholar
Mironov, D. V. 2001 Pressure-potential-temperature covariance in convection with rotation. Q. J. R. Meteorol. Soc. 127 (571, Part a), 89–110.Google Scholar
Mironov, D. V., Gryanik, V. M., Moeng, C.-H., Olbers, D. J. & Warncke, T. H. 2000 Vertical turbulence structure and second-moment budgets in convection with rotation: a large-eddy simulation study. Q. J. R. Meteor. Soc. 126 (563), 477–515.10.1002/qj.49712656306Google Scholar
Mironov, D. V. 2009 Turbulence in the lower troposphere: second-order closure and mass-flux modelling frameworks. In Interdisciplinary Aspects of Turbulence (ed. Hillebrandt, W. & Kupka, F.), Lecture Notes in Physics, vol. 756, pp. 161–221.Google Scholar
Moeng, C. H. & Wyngaard, J. C. 1986 An analysis of closures for pressure-scalar covariances in the convective boundary layer. J. Atmos. Sci. 43 (21), 2499–2513.Google Scholar
Pearson, B. C. 2018 Turbulence-induced anti-stokes flow and the resulting limitations of large-eddy simulation. J. Phys. Oceanogr. 48 (1), 117–122.Google Scholar
Pearson, B. C., Grant, A. L. M., Polton, J. A. & Belcher, S. E. 2015 Langmuir turbulence and surface heating in the ocean surface boundary layer. J. Phys. Oceanogr. 45 (12), 2897–2911.Google Scholar
Phillips, O. M. 1958 The equilibrium range in the spectrum of wind-generated waves. J. Fluid Mech. 4 (4), 426–434.Google Scholar
Polton, J. A., Lewis, D. M. & Belcher, S. E. 2005 The role of wave-induced Coriolis-Stokes forcing on the wind-driven mixed layer. J. Phys. Oceanogr. 35 (4), 444–457.10.1175/JPO2701.1Google Scholar
Polton, J. A. & Belcher, S. E. 2007 Langmuir turbulence and deeply penetrating jets in an unstratified mixed layer. J. Geophys. Res. 112, C09020.Google Scholar
Pope, S. B. 2001 Turbulent Flows. Cambridge University Press.Google Scholar
Poroseva, S. V. 2001 Modeling the‘rapid’ part of the velocity/pressure-gradient correlation in inhomogeneous turbulence. Centre for Turbulence Research, Ann. Res. Briefs.Google Scholar
Poroseva, S. V. 2014 The effect of a pressure-containing correlation model on near-wall flow simulations with Reynolds stress transport models. Trans. ASME J. Fluids Engng 136 (6), 060909.Google Scholar
Reichl, B. G., Wang, D., Hara, T., Ginis, I. & Kukulka, T. 2016 Langmuir turbulence parameterization in tropical cyclone conditions. J. Phys. Oceanogr. 46 (3), 863–886.10.1175/JPO-D-15-0106.1Google Scholar
Roekel, L. P. V., Fox-Kemper, B., Sullivan, P. P., Hamlington, P. E. & Haney, S. R. 2012 The form and orientation of Langmuir cells for mis-aligned winds and waves. J. Geophys. Res. 117, CO5001.Google Scholar
Rotta, J. 1951 Statistische Theorie nichthomogener Turbulenz. Z. Phys. 129 (6), 547–572.Google Scholar
Shutts, G. J. & Gray, M. E. B. 1994 A numerical modelling study of the geostrophic adjustment process following deep convection. Q. J. R. Meteorol. Soc. 120 (519), 1145–1178.Google Scholar
Skyllingstad, E. & Denbo, D. 1995 An ocean large-eddy simulation of langmuir circulations and convection in the surface mixed layer. J. Geophys. Res. 100 (C5), 8501–8522.10.1029/94JC03202Google Scholar
Speziale, C. G., Sarkar, S. & Gatski, T. B. 1991 Modeling the pressure–strain correlation of turbulence: an invariant dynamic-systems approach. J. Fluid Mech. 227, 245–272.Google Scholar
Stokes, G. G. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441–473.Google Scholar
Sullivan, P. P. & McWilliams, J. C. 2018 Frontogenesis and frontal arrest of a dense filament in the oceanic surface boundary layer. J. Fluid Mech. 837, 341–380.10.1017/jfm.2017.833Google Scholar
Sutherland, G., Christensen, K. H. & Ward, B. 2014 Evaluating Langmuir turbulence parameterizations in the ocean surface boundary layer. J. Geophys. Res. 119 (3), 1899–1910.Google Scholar
Suzuki, N. & Fox-Kemper, B. 2016 Understanding Stokes forces in the wave-averaged equations. J. Geophys. Res. 121 (5), 3579–3596.Google Scholar
Teixeira, M. A. C. 2011 A linear model for the structure of turbulence beneath surface water waves. Ocean Model. 36 (1–2), 149–162.10.1016/j.ocemod.2010.10.007Google Scholar
Teixeira, M. A. C. & Belcher, S. E. 2002 On the distortion of turbulence by a progressive surface wave. J. Fluid Mech. 458, 229–267.10.1017/S0022112002007838Google Scholar
Teixeira, M. A. C. & Belcher, S. E. 2010 On the structure of Langmuir turbulence. Ocean Model. 31 (3–4), 105–119.Google Scholar
Townsend, A. A. 1954 The uniform distortion of homogeneous turbulence. Q. J. Mech. Appl. Maths. 7, 104–127.10.1093/qjmam/7.1.104Google Scholar
Tseng, R.-S. & D’Asaro, E. A. 2004 Measurements of turbulent vertical kinetic energy in the ocean mixed layer from Lagrangian floats. J. Phys. Oceanogr. 34 (9), 1984–1990.Google Scholar
Uberoi, M. S. 1957 Equipartition of energy and local isotropy in turbulent flows. J. Appl. Phys. 28 (10), 1165–1170.10.1063/1.1722600Google Scholar
Umlauf, L. & Burchard, H. 2005 Second-order turbulence closure models for geophysical boundary layers. A review of recent work. Cont. Shelf Res. 25 (7–8), 795–827.Google Scholar
Webb, A. & Fox-Kemper, B. 2011 Wave spectral moments and Stokes drift estimation. Ocean Model. 40 (3), 273–288.10.1016/j.ocemod.2011.08.007Google Scholar
Weinstock, J. & Burk, S. 1985 Theoretical pressure–strain term, experimental comparison, and resistance to large anisotropy. J. Fluid Mech. 154 (MAY), 429–443.Google Scholar