Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T09:33:54.401Z Has data issue: false hasContentIssue false
  • English
  • Français

Pressure-driven flow across a hyperelastic porous membrane

Published online by Cambridge University Press:  24 May 2019

Ryungeun Song Open the ORCID record for Ryungeun Song [Opens in a new window] ,
Howard A. Stone Open the ORCID record for Howard A. Stone [Opens in a new window] ,
Kaare H. Jensen Open the ORCID record for Kaare H. Jensen [Opens in a new window]  and
Jinkee Lee Open the ORCID record for Jinkee Lee [Opens in a new window]
Ryungeun Song
Affiliation:
School of Mechanical Engineering, Sungkyunkwan University, Suwon, Gyeonggi-do 16419, Republic of Korea
Howard A. Stone
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Kaare H. Jensen
Affiliation:
Department of Physics, Technical University of Denmark, Kongens Lyngby, DK-2800, Denmark
Jinkee Lee*
Affiliation:
School of Mechanical Engineering, Sungkyunkwan University, Suwon, Gyeonggi-do 16419, Republic of Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

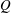We report an experimental investigation of pressure-driven flow of a viscous liquid across thin polydimethylsiloxane (PDMS) membranes. Our experiments revealed a nonlinear relation between the flow rate $Q$ and the applied pressure drop 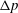$\unicode[STIX]{x0394}p$, in apparent disagreement with Darcy’s law, which dictates a linear relationship between flow rate, or average velocity, and pressure drop. These observations suggest that the effective permeability of the membrane decreases with pressure due to deformation of the nanochannels in the PDMS polymeric network. We propose a model that incorporates the effects of pressure-induced deformation of the hyperelastic porous membrane at three distinct scales: the membrane surface area, which increases with pressure, the membrane thickness, which decreases with pressure, and the structure of the porous material, which is deformed at the nanoscale. With this model, we are able to rationalize the deviation between Darcy’s law and the data. Our result represents a novel case in which macroscopic deformations can impact the microstructure and transport properties of soft materials.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 742 - 754
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amabili, M., Balasubramanian, P., Breslavsky, I. D., Ferrari, G., Garziera, R. & Riabova, K. 2016 Experimental and numerical study on vibrations and static deflection of a thin hyperelastic plate. J. Sound Vib. 385, 81–92.Google Scholar
Bhanushali, D., Kloos, S., Kurth, C. & Bhattacharyya, D. 2001 Performance of solvent-resistant membranes for non-aqueous systems: solvent permeation results and modeling. J. Membr. Sci. 189 (1), 1–21.Google Scholar
Bouremel, Y., Madaan, S., Lee, R. M. H., Eames, I., Wojcik, A. & Khaw, P. T. 2017 Pursing of planar elastic pockets. J. Fluids Struct. 70, 261–275.Google Scholar
Bruus, H. 2007 Theoretical Microfluidics. Oxford University Press.Google Scholar
Chang, K. S., Chung, Y. C., Yang, T. H., Lue, S. J., Tung, K. L. & Lin, Y. F. 2012 Free volume and alcohol transport properties of PDMS membranes: insights of nano-structure and interfacial affinity from molecular modeling. J. Membr. Sci. 417, 119–130.Google Scholar
Choi, C. H., Westin, K., Johan, A. & Breuer, K. 2003 Apparent slip flows in hydrophilic and hydrophobic microchannels. Phys. Fluids 15 (10), 2897–2902.Google Scholar
Darvishmanesh, S., Buekenhoudt, A., Degrève, J. & Van der Bruggen, B. 2009 General model for prediction of solvent permeation through organic and inorganic solvent resistant nanofiltration membranes. J. Membr. Sci. 334 (1), 43–49.Google Scholar
Dhopeshwarkar, R., Crooks, R., Hlushkou, D. & Tallarek, U. 2008 Transient effects on microchannel electrokinetic filtering with an ion-permselective membrane. Anal. Chem. 80 (4), 1039–1048.Google Scholar
Duffy, D. C., McDonald, J. C., Schueller, O. J. A. & Whitesides, G. M. 1998 Rapid prototyping of microfluidic systems in poly(dimethylsiloxane). Anal. Chem. 70 (23), 4974–4984.Google Scholar
Ebert, K., Koll, J., Dijkstra, M. F. J. & Eggers, M. 2006 Fundamental studies on the performance of a hydrophobic solvent stable membrane in non-aqueous solutions. J. Membr. Sci. 285 (1), 75–80.Google Scholar
Firpo, G., Angeli, E., Repetto, L. & Valbusa, U. 2015 Permeability thickness dependence of polydimethylsiloxane (PDMS) membranes. J. Membr. Sci. 481, 1–8.Google Scholar
Gangi, A. F. 1978 Variation of whole and fractured porous rock permeability with confining pressure. Intl J. Rock Mech. Min Sci. Geomech. Abstr. 15 (5), 249–257.Google Scholar
Geens, J., Van der Bruggen, B. & Vandecasteele, C. 2004 Characterisation of the solvent stability of polymeric nanofiltration membranes by measurement of contact angles and swelling. Chem. Engng Sci. 59 (5), 1161–1164.Google Scholar
Hu, H., Bao, L., Priezjev, N. V. & Luo, K. 2017 Identifying two regimes of slip of simple fluids over smooth surfaces with weak and strong wall–fluid interaction energies. J. Chem. Phys. 146 (3), 034701.Google Scholar
Ismail, A. E., Grest, G. S., Heine, D. R., Stevens, M. J. & Tsige, M. 2009 Interfacial structure and dynamics of siloxane systems: PDMS-vapor and PDMS-water. Macromolecules 42 (8), 3186–3194.Google Scholar
Jeong, O. C. & Konishi, S. 2007 Fabrication and drive test of pneumatic PDMS micro pump. Sensors Actuators A 135 (2), 849–856.Google Scholar
Jo, B. H., Van Lerberghe, L. M., Motsegood, K. M. & Beebe, D. J. 2000 Three-dimensional micro-channel fabrication in polydimethylsiloxane (PDMS) elastomer. J. Microelectromech. Syst. 9 (1), 76–81.Google Scholar
Johnston, I. D., McCluskey, D. K., Tan, C. K. L. & Tracey, M. C. 2014 Mechanical characterization of bulk Sylgard 184 for microfluidics and microengineering. J. Micromech. Microengng 24 (3), 035017.Google Scholar
Koresh, J. E. & Sofer, A. 1983 Molecular sieve carbon permselective membrane. Part I. Presentation of a new device for gas mixture separation. Sep. Sci. Technol. 18 (8), 723–734.Google Scholar
Makrodimitri, Z. A. & Economou, I. G. 2008 Atomistic simulation of poly(dimethylsiloxane) permeability properties to gases and n-alkanes. Macromolecules 41 (15), 5899–5907.Google Scholar
Nunes, L. C. S. 2011 Mechanical characterization of hyperelastic polydimethylsiloxane by simple shear test. Mater. Sci. Engng A 528 (3), 1799–1804.Google Scholar
Peng, F., Jiang, Z., Hu, C., Wang, Y., Xu, H. & Liu, J. 2006 Removing benzene from aqueous solution using CMS-filled PDMS pervaporation membranes. Sep. Purif. Technol. 48 (3), 229–234.Google Scholar
Pernaut, J. M. & Reynolds, J. R. 2000 Use of conducting electroactive polymers for drug delivery and sensing of bioactive molecules. A redox chemistry approach. J. Phys. Chem. B 104 (17), 4080–4090.Google Scholar
Phillip, W. A., Amendt, M., O’Neill, B., Chen, L., Hillmyer, M. A. & Cussler, E. L. 2009 Diffusion and flow across nanoporous polydicyclopentadiene-based membranes. ACS Appl. Mater. Interfaces 1 (2), 472–480.Google Scholar
Priezjev, N. V. 2007 Effect of surface roughness on rate-dependent slip in simple fluids. J. Chem. Phys. 127 (14), 144708.Google Scholar
Priske, M., Lazar, M., Schnitzer, C. & Baumgarten, G. 2016 Recent applications of organic solvent nanofiltration. Chem. Ing. Tech. 88 (1–2), 39–49.Google Scholar
Ramos-Alvarado, B., Kumar, S. & Peterson, G. P. 2016 Wettability transparency and the quasiuniversal relationship between hydrodynamic slip and contact angle. Appl. Phys. Lett. 108 (7), 074105.Google Scholar
Razdolsky, A. G. 2015 Large deflections of elastic rectangular plates. Intl J. Comput. Meth. Engng Sci. Mech. 16 (6), 354–361.Google Scholar
Rego, R. & Mendes, A. 2004 Carbon dioxide/methane gas sensor based on the permselectivity of polymeric membranes for biogas monitoring. Sensors Actuators B 103 (1), 2–6.Google Scholar
Robinson, J. P., Tarleton, E. S., Ebert, K., Millington, C. R. & Nijmeijer, A. 2005 Influence of cross-linking and process parameters on the separation performance of poly(dimethylsiloxane) nanofiltration membranes. Ind. Engng Chem. Res. 44 (9), 3238–3248.Google Scholar
Sanaei, P. & Cummings, L. J. 2017 Flow and fouling in membrane filters: effects of membrane morphology. J. Fluid Mech. 818, 744–771.Google Scholar
Sanaei, P. & Cummings, L. J. 2018 Membrane filtration with complex branching pore morphology. Phys. Rev. Fluids 3, 094305.Google Scholar
Selvadurai, A. P. S. & Shi, M. 2012 Fluid pressure loading of a hyperelastic membrane. Intl J. Non-Linear Mech. 47 (2), 228–239.Google Scholar
Soltane, H. B., Roizard, D. & Favre, E. 2013 Effect of pressure on the swelling and fluxes of dense PDMS membranes in nanofiltration: an experimental study. J. Membr. Sci. 435, 110–119.Google Scholar
Stafie, N., Stamatialis, D. F. & Wessling, M. 2005 Effect of PDMS cross-linking degree on the permeation performance of PAN/PDMS composite nanofiltration membranes. Sep. Purif. Technol. 45 (3), 220–231.Google Scholar
Tsuru, T., Sudou, T., Kawahara, S., Yoshioka, T. & Asaeda, M. 2000 Permeation of liquids through inorganic nanofiltration membranes. J. Colloid Interface Sci. 228 (2), 292–296.Google Scholar
Vankelecom, I. F. J., De Smet, K., Gevers, L. E. M., Livingston, A., Nair, D., Aerts, S., Kuypers, S. & Jacobs, P. A. 2004 Physico-chemical interpretation of the SRNF transport mechanism for solvents through dense silicone membranes. J. Membr. Sci. 231 (1), 99–108.Google Scholar
Vankelecom, I. F. J., Dotremont, C., Morobe, M., Uytterhoeven, J. B. & Vandecasteele, C. 1997 Zeolite-filled PDMS membranes. 1. Sorption of halogenated hydrocarbons. J. Phys. Chem. B 101 (12), 2154–2159.Google Scholar
Wang, D. & El-Sheikh, A. I. 2005 Large-deflection mathematical analysis of rectangular plates. J. Engng Mech. ASCE 131 (8), 809–821.Google Scholar
Zhang, J., Standifird, W. B., Roegiers, J. C. & Zhang, Y. 2007 Stress-dependent fluid flow and permeability in fractured media: from lab experiments to engineering applications. Rock Mech. Rock Engng 40 (1), 3–21.Google Scholar