Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T17:48:25.190Z Has data issue: false hasContentIssue false
  • English
  • Français

Pressure forces on sediment particles in turbulent open-channel flow: a laboratory study

Published online by Cambridge University Press:  19 September 2014

Mohammad Amir ,
Vladimir I. Nikora  and
Mark T. Stewart
Mohammad Amir*
Affiliation:
School of Engineering, University of Aberdeen, Aberdeen AB24 3UE, UK
Vladimir I. Nikora
Affiliation:
School of Engineering, University of Aberdeen, Aberdeen AB24 3UE, UK
Mark T. Stewart
Affiliation:
School of Engineering, University of Aberdeen, Aberdeen AB24 3UE, UK
*
†Present address: Silixa Ltd, Silixa House, 230 Centennial Park, Centennial Avenue, Elstree WD6 3SN, UK. Email address for correspondence: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An experimental investigation into the fluctuating pressure acting on sediment particles on the bed of an open-channel flow was carried out in a large laboratory flume for a range of flow depths and bed slopes. The pressure measurements were made using 23 spherical particles instrumented with differential pressure sensors. These measurements were complemented with simultaneous measurements of the velocity field using high-resolution stereoscopic particle image velocimetry. The pressure statistics show that the standard deviations of the drag and lift fluctuations vary from 2.0 to 2.6 and from 2.5 to 3.4 times the wall shear stress, respectively, and are dependent on relative submergence and flow Reynolds number. The skewness is positive for the drag fluctuations and negative for the lift fluctuations. The kurtosis values of both drag and lift fluctuations increase with particle submergence. The two-particle correlation between drag and lift fluctuations is found to be relatively weak compared to the two-point drag–drag and lift–lift correlations. The pressure cross-correlations between particles separated in the longitudinal direction exhibit maxima at certain time delays corresponding to the convection velocities varying from 0.64 to 0.72 times the bulk flow velocity, being very close to the near-bed eddy convection velocities. The temporal autocorrelation of drag fluctuations decays much faster than that for the lift fluctuations; as a result, the temporal scales of lift fluctuations are 3–6 times that of drag fluctuations. The spatial and temporal scales of both drag and lift fluctuations show dependence on flow depth and bed slope. The spectral behaviour of both drag and lift fluctuations is also assessed. A 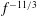$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}f^{-11/3}$ slope is observed for the spectra of the drag fluctuations over the majority of the frequency range, whereas the lift spectra suggest two scaling ranges, following a 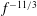$f^{-11/3}$ slope at high frequencies and 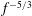$f^{-5/3}$ behaviour at lower frequencies.

JFM classification

Waves/Free-surface Flows: Channel flow Geophysical and Geological Flows: Sediment transport Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 458 - 497
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© 2014 Cambridge University Press

References

Adrian, A. J. 2007 Hairpin vortex organisation in wall turbulence. Phys. Fluids 19 (4), 1–16.CrossRefGoogle Scholar
Adrian, A. J. & Marusic, I. 2012 Coherent structures in flow over hydraulic engineering surfaces. J. Hydraul Res. 50 (5), 451–464.CrossRefGoogle Scholar
Bajsic, I., Kutin, J. & Zagar, T. 2007 The response time of a pressure measurement system with a connecting tube. Instrum. Sci. Technol. 35, 399–409.CrossRefGoogle Scholar
Blake, W. K. 1970 Turbulent boundary-layer wall-pressure fluctuations on smooth and rough walls. J. Fluid Mech. 44 (4), 637–660.CrossRefGoogle Scholar
Burton, T. E.1973 Wall pressure fluctuations at smooth and rough surfaces under turbulent boundary layers with favourable and adverse pressure gradients. Report Ad-772 548. Office of Naval Research.CrossRefGoogle Scholar
Cameron, S. M.2006 Near boundary flow structure and particle entrainment. PhD dissertation, University of Auckland, New Zealand.Google Scholar
Cameron, S. M. 2011 PIV algorithms for open-channel turbulence research: accuracy, resolution and limitations. J. Hydro-Environ. Res. 5 (4), 246–262.CrossRefGoogle Scholar
Cameron, S. M. & Nikora, V. 2008 Eddy convection velocity for smooth- and rough-bed open-channel flows: particle image velocimetry study. In River Flow 2008, Proceedings of the International Conference on Fluvial Hydraulics, Cesme-izmir-Turkey, pp. 143–150. A. A. Balkema.Google Scholar
Cameron, S. M., Nikora, V. I., Albayrak, I., Miler, O., Stewart, M. & Siniscalchi, F. 2013 Interactions between aquatic plants and turbulent flow: a field study using a stereoscopic PIV system. J. Fluid Mech. 732, 345–372.CrossRefGoogle Scholar
Cantwell, B. J. 1981 Organised motion in turbulent flow. Rev. Fluid Mech. 13, 457–515.CrossRefGoogle Scholar
Celik, A. O., Diplas, P. & Dancey, C. 2014 Instantaneous pressure measurements on a spherical grain under threshold flow conditions. J. Fluid Mech. 741, 60–97.CrossRefGoogle Scholar
Chan-Braun, C.2012 Turbulent open channel flow, sediment erosion and sediment transport. PhD dissertation, University of Karlsruhe, Germany.Google Scholar
Chan-Braun, C., Villalba, M. G. & Uhlmann, M. 2011 Force and torque acting on particles in a transitionally rough open channel flow. J. Fluid Mech. 684, 441–474.CrossRefGoogle Scholar
Chan-Braun, C., Villalba, M. G. & Uhlmann, M. 2013 Spatial and temporal scales of force and torque acting on wall-mounted spherical particles in open channel flow. Phys. Fluids 25, 075103.CrossRefGoogle Scholar
Chepil, W. S. 1958 The use of evenly spaced hemispheres to evaluate aerodynamic forces on a soil surface. EOS Trans. AGU 39, 397–404.Google Scholar
Chepil, W. S. 1961 The use of spheres to measure lift and drag on wind-eroded soil grains. Soil Sci. Soc. Am. J. 25, 343–345.CrossRefGoogle Scholar
Coleman, N. L. 1967 A theoretical and experimental study of drag and lift forces acting on a sphere resting on a hypothetical stream bed. In Proceedings of 12th IAHR Congress, vol. 3, pp. 185–192. Fort Collins.Google Scholar
Coleman, N. L. & Ellis, W. M. 1976 Model study of the drag coefficient of a streambed particle. In Proceedings of 3rd Federal Interagency Sedimentation Conference, Denver, USA. Water Resources Council, National Technical Information Service, Springfield, VA, USA, 4/1–4/11.Google Scholar
Detert, M.2008 Hydrodynamic processes at the water–sediment interface of streambeds. PhD thesis, University of Karlsruhe, Germany.Google Scholar
Detert, M., Jirka, G. H., Klar, M., Jehle, M., Jahne, B., Kohler, H.-J. & Wenka, T. 2004 Pressure fluctuations within subsurface gravel bed caused by turbulent open-channel flow. In River Flow 2004, Proceedings of the International Conference on Fluvial Hydraulics, Napoli (ed. Greco, M., Carravetta, A. & Della Morte, R.). A. A. Balkema.Google Scholar
Detert, M., Weitbrecht, V. & Jirka, G. H. 2010a Laboratory measurements on turbulent pressure fluctuations in and above gravel beds. J. Hydraul. Engng ASCE 136 (10), 779–789.CrossRefGoogle Scholar
Detert, M., Nikora, V. & Jirka, G. H. 2010b Synoptic velocity and pressure fields at the water–sediment interface of streambeds. J. Fluid Mech. 660, 55–86.CrossRefGoogle Scholar
Diplas, P., Dancey, C. L., Celik, A. O., Valyrakis, M., Greer, K. & Akar, T. 2008 The role of impulse on the initiation of particle movement under turbulent flow conditions. Science 322, 717–720.CrossRefGoogle ScholarPubMed
Dwivedi, A.2010 Mechanics of sediment entrainment. PhD thesis, University of Auckland, New Zealand.Google Scholar
Dwivedi, A., Melville, B. & Shamseldin, A. Y. 2010 Hydrodynamic forces generated on a spherical sediment particle during entrainment. J. Hydraul. Engng ASCE 136, 756–769.CrossRefGoogle Scholar
Ecklemann, H. 1988 A review of knowledge on pressure fluctuations. In Proceedings of Zoran Zaric Memorial International Seminar on Near-Wall Turbulence, Dubrovnik, Yugoslavia, vol. 28, pp. 328–347.Google Scholar
Einstein, H. A. & El-Samni, E. A. 1949 Hydrodynamic forces on a rough wall. Rev. Mod. Phys. 21 (3), 520–523.CrossRefGoogle Scholar
Farabee, T. M. & Casarella, M. J. 1991 Spectral features of wall pressure fluctuations beneath turbulent boundary layers. Phys. Fluids 3, 2410–2420.CrossRefGoogle Scholar
Garcia, C. M., Jackson, P. R. & Garcia, M. H. 2006 Confidence intervals in the determination of turbulence parameters. Exp. Fluids 40, 514–522.CrossRefGoogle Scholar
Garcia, M., Nino, Y. & Lopez, F. 1995 Characterisation of near-bed coherent structures in turbulent open channel flow using synchronised high-speed video and hot-film measurements. Exp. Fluids 19, 16–28.CrossRefGoogle Scholar
Garcia, M., Nino, Y. & Lopez, F. 1996 Laboratory observations of particle entrainment into suspension by turbulent bursting. In Coherent Flow Structures in Open Channels (ed. Ashworth, P. J., Bennet, S. J., Best, J. I. & McLelland, S. J.), pp. 63–84. Wiley.Google Scholar
George, W. K., Beuther, P. D. & Arndt, R. E. A. 1984 Pressure spectra in turbulent free shear flows. J. Fluid Mech. 148, 148–191.CrossRefGoogle Scholar
Grass, A. J. 1971 Structural features of turbulent flow over smooth and rough boundaries. J. Fluid Mech. 50, 230–255.CrossRefGoogle Scholar
Hinze, J. O. 1975 Turbulence. McGraw-Hill.Google Scholar
Hofland, B.2005 Rock and roll, turbulence-induced damage of granular bed predictions. PhD thesis, Delft University of Technology, The Netherlands.Google Scholar
Hofland, B., Battjes, J. & Booij, R. 2005 Measurement of fluctuating pressures on coarse bed material. J. Hydraul. Engng ASCE 131 (9), 770–781.CrossRefGoogle Scholar
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.CrossRefGoogle Scholar
Irwin, H. P. A. H., Cooper, K. R. & Girard, R. 1979 Correction of distortion effects caused by tubing systems in measurements of fluctuating pressures. J. Wind Engng Ind. Aerodyn. 5, 93–107.CrossRefGoogle Scholar
Katul, G. G. & Parlange, M. B. 1995 Analysis of land surface heat fluxes using the orthonormal wavelet approach. Water Resour. Res. 31, 2743–2749.CrossRefGoogle Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel flow. J. Fluid Mech. 205, 421–451.CrossRefGoogle Scholar
Kline, S. J. 1978 The role of visualisation in the study of the structure of the turbulent boundary layer. In Lehigh Workshop on Coherent Structure of Turbulent Boundary Layers (ed. Smith, C. R. & Abbott, D. E.), p. 126. Lehigh University.Google Scholar
Kraichnan, R. H. 1956 Pressure fluctuations in turbulent flow over a flat plate. J. Acoust. Soc. Am. 28, 378–390.CrossRefGoogle Scholar
Lamb, M. P., Dietrich, W. E. & Venditti, J. G. 2008 Is the critical shields stress for incipient sediment motion dependent on channel-bed slope? J. Geophys. Res. 113, F02008.Google Scholar
Lee, I. & Sung, H. J. 2002 Multiple-arrayed pressure measurement for investigation of the unsteady flow structure of a reattaching shear layer. J. Fluid Mech. 463, 377–402.CrossRefGoogle Scholar
Manes, C., Pokrajac, D. & McEwan, I. 2007 Double-averaged open-channel flows with small relative submergence. J. Hydraul. Engng ASCE 133 (8), 896–904.CrossRefGoogle Scholar
Mattioli, M., Alsina, J. M., Mancinelli, A., Miozzi, M. & Brocchini, M. 2012 Experimental investigation of the nearbed dynamics around a submarine pipeline laying on different types of seabed: the interaction between turbulent structures and particles. Adv. Water Resour. 48, 31–46.CrossRefGoogle Scholar
Moffat, R. J. 1988 Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1, 3–17.CrossRefGoogle Scholar
Nelson, J., Shreve, R. L., McLean, S. R. & Drake, T. G. 1995 Role of near-bed turbulence structure in bed load transport and bed-form mechanics. Water Resour. Res. 31 (8), 2071–2086.CrossRefGoogle Scholar
Nezu, I. 2005 Open-channel flow turbulence and its research prospect in the 21st century. J. Hydraul. Engng ASCE 131 (4), 229–246.CrossRefGoogle Scholar
Nezu, I. & Nakagawa, H. 1993 Turbulence in Open-Channel Flows. Balkema.Google Scholar
Nikora, V. & Goring, D. 2000 Eddy convection velocity and Taylor’s hypothesis of ‘frozen’ turbulence in a rough-bed open-channel flow. J. Hydrosci. Hydraul. Engng 18 (2), 75–91.Google Scholar
Nikora, V., McEwan, I., McLean, S., Coleman, S., Pokrajac, D. & Walters, R. 2007a Double-averaging concept for rough-bed open-channel and overland flows: theoretical background. J. Hydraul. Engng ASCE 133 (8), 873–883.CrossRefGoogle Scholar
Nikora, V., McLean, S., Coleman, S., Pokrajac, D., McEwan, I., Campbell, L., Aberle, J., Clunie, D. & Koll, K. 2007b Double-averaging concept for rough-bed open-channel and overland flows: applications. J. Hydraul. Engng ASCE 133 (8), 884–895.CrossRefGoogle Scholar
Nino, Y. & Garcia, M. H. 1996 Experiments on particle–turbulence interactions in the near-wall region of an open-channel flow: implications for sediment transport. J. Fluid Mech. 326, 285–319.CrossRefGoogle Scholar
Pokrajac, D., Finnigan, J. J., Manes, C., McEwan, I. & Nikora, V. 2006 On the definition of the shear velocity in rough bed open channel flows. In River Flow 2006, Proceedings of the International Conference on Fluvial Hydraulics, Lisbon, Portugal, pp. 88–96. Taylor & Francis.Google Scholar
Prasad, A. K. 2000 Stereoscopic particle image velocimetry. Exp. Fluids 29, 103–116.CrossRefGoogle Scholar
Quadrio, M. & Luchini, P. 2003 Integral space–time scales in turbulent wall flows. Phys. Fluids 15 (8), 2219–2227.CrossRefGoogle Scholar
Rashidi, M., Hetsroni, G. & Banerjee, S. 1990 Particle–turbulence interaction in a boundary layer. Intl J. Multiphase Flow 16, 935–949.CrossRefGoogle Scholar
Raudkivi, A. J. 1990 Loose Boundary Hydraulics, 3rd edn. Pergamon.Google Scholar
Robinson, S. K. 1991 Coherent motions in turbulent boundary layers. Annu. Rev. Fluid Mech. 13, 601–639.CrossRefGoogle Scholar
Schewe, G. 1983 On the force fluctuations acting on a circular cylinder in crossflow from subcritical to transcritical Reynolds numbers. J. Fluid Mech. 134, 311–328.CrossRefGoogle Scholar
Schmeeckle, M. W., Nelson, J. M. & Shreve, R. L. 2007 Forces on stationary particles in near-bed turbulent flows. J. Geophys. Res. 112, F02003.Google Scholar
Shields, A.1936 Anwendung der Ahnlichkeitsmechanik und der Turbulentzforschung auf die Geshiebebewegung, Mitt. Preuss. Versuchsanst. Wasserbau Schiffbau, vol. 26, 26 pp. (English translation by W. P. Ott & J. C. van Uchelen, 1936. Rep. 167, 36 pp., Calif. Inst. of Technol., Pasadena).Google Scholar
Singh, K. M., Sandham, N. D. & Williams, J. J. R. 2007 Numerical simulation of flow over a rough bed. J. Hydraul. Engng ASCE 133, 386–398.CrossRefGoogle Scholar
Smart, G. M. 2005 A novel gravel entrainment investigation. In Proceedings of the 4th IAHR Symposium on River, Coastal and Estuarine Morphodynamics, Urbana, Illinois, USA. Taylor & Francis.Google Scholar
Smart, G. M. 2008 Pressure fluctuations and entrainment on a gravel bed. In River Flow 2008, International Conference on Fluvial Hydraulics, Cesme-izmir-Turkey (ed. Altinakar, M. S., Kokpinar, M. A., Aydin, I., Cokgor, S. & Kirkgoz, S.). A. A. Balkema.Google Scholar
Smart, G. M. & Habersack, H. M. 2007 Pressure fluctuations and gravel entrainment in rivers. J. Hydraul Res. 45 (5), 661–673.CrossRefGoogle Scholar
Stewart, M. T.2014 Turbulence structure of rough-bed open-channel flow. PhD dissertation, University of Aberdeen, UK.Google Scholar
Sumer, B. M. & Deigaard, R. 1981 Particle motions near the bottom in turbulent flow in an open channel. J. Fluid Mech. 109, 311–338.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Tritton, D. J. 1988 Physical Fluid Dynamics, 2nd edn. Oxford University Press.Google Scholar
Tsuji, Y., Fransson, J. H. M., Alfredsson, P. H. & Johansson, A. V. 2007 Pressure statistics and their scaling in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 585, 1–40.CrossRefGoogle Scholar
Van Hout, R. 2013 Spatially and temporally resolved measurements of bead resuspension and saltation in a turbulent water channel flow. J. Fluid Mech. 715, 389–423.CrossRefGoogle Scholar
Welch, P. D. 1967 The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15, 70–73.CrossRefGoogle Scholar
Willert, C. 1997 Stereoscopic digital particle image velocimetry for application in wind tunnel flows. Meas. Sci. Technol. 8, 1465–1479.CrossRefGoogle Scholar
Willmarth, W. W. 1975 Structure of turbulence in boundary layers. Adv. Appl. Mech. 15, 159–254.CrossRefGoogle Scholar
Willmarth, W. W. & Roos, F. W. 1965 Resolution and structure of the wall pressure field beneath a turbulent boundary layer. J. Fluid Mech. 22, 81–94.CrossRefGoogle Scholar
Willmarth, W. W. & Wooldridge, C. E. 1962 Measurements of the fluctuating pressure at the wall beneath a thick turbulent boundary layer. J. Fluid Mech. 14 (2), 187–210.CrossRefGoogle Scholar
Yoshida, A., Tamura, Y. & Kurita, T. 2001 Effects of bends in a tubing system for pressure measurement. J. Wind Engng Ind. Aerodyn. 89 (20), 1701–1716.Google Scholar
Yung, B. P. K., Merry, H. & Bott, T. R. 1989 The role of turbulent bursts in particle re-entrainment in aqueous systems. Chem. Engng Sci. 44, 873–882.CrossRefGoogle Scholar