Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-13T22:35:36.978Z Has data issue: false hasContentIssue false
  • English
  • Français

The preferred mode of incompressible jets: linear frequency response analysis

Published online by Cambridge University Press:  25 January 2013

X. Garnaud ,
L. Lesshafft ,
P. J. Schmid  and
P. Huerre
X. Garnaud*
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), Ecole Polytechnique – CNRS, 91128 Palaiseau, France
L. Lesshafft
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), Ecole Polytechnique – CNRS, 91128 Palaiseau, France
P. J. Schmid
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), Ecole Polytechnique – CNRS, 91128 Palaiseau, France
P. Huerre
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), Ecole Polytechnique – CNRS, 91128 Palaiseau, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

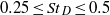The linear amplification of axisymmetric external forcing in incompressible jet flows is investigated within a fully non-parallel framework. Experimental and numerical studies have shown that isothermal jets preferably amplify external perturbations for Strouhal numbers in the range $0. 25\leq {\mathit{St}}_{D} \leq 0. 5$, depending on the operating conditions. In the present study, the optimal forcing of an incompressible jet is computed as a function of the excitation frequency. This analysis characterizes the preferred amplification as a pseudo-resonance with a dominant Strouhal number of around $0. 45$. The flow response at this frequency takes the form of a vortical wavepacket that peaks inside the potential core. Its global structure is characterized by the cooperation of local shear-layer and jet-column modes.

JFM classification

Instability: Instability Wakes/Jets: Jets Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , pp. 189 - 202
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alizard, F., Cherubini, S. & Robinet, J.-C. 2009 Sensitivity and optimal forcing response in separated boundary layer flows. Phys. Fluids 21 (6), 064108.Google Scholar
Andersson, P., Berggren, M. & Henningson, D. S. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11 (1), 134.CrossRefGoogle Scholar
Balay, S., Buschelman, K., Eijkhout, V., Gropp, W. D., Kaushik, D., Knepley, M. G., McInnes, L. C., Smith, B. F. & Zhang, H. 2008 PETSc users’ manual. Tech. Rep. ANL-95/11, Revision 3.0.0. Argonne National Laboratory, available athttp://www.mcs.anl.gov/petsc/petsc-as/.Google Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Batchelor, G. K. & Gill, A. E. 1962 Analysis of the stability of axisymmetric jets. J. Fluid Mech. 14 (4), 529.Google Scholar
Cooper, A. J. & Crighton, D. G. 2000 Global modes and superdirective acoustic radiation in low-speed axisymmetric jets. Eur. J. Mech. B 19 (5), 559–574.Google Scholar
Crighton, D. G. & Gaster, M. 1976 Stability of slowly diverging jet flow. J. Fluid Mech. 77 (2), 397.Google Scholar
Crow, S. C. & Champagne, F. H. 1971 Orderly structure in jet turbulence. J. Fluid Mech. 48 (3), 547.Google Scholar
Dick, E. 2009 Introduction to finite element methods in computational fluid dynamics. In Computational Fluid Dynamics: An Introduction, 3rd edn. Springer.Google Scholar
Garnaud, X. 2012 Modes, transient dynamics and forced response of circular jets. PhD thesis, Ecole Polytechnique.Google Scholar
Garnaud, X., Lesshafft, L. & Huerre, P. 2011 Global linear stability of a model subsonic jet. AIAA Paper 2011-3608.CrossRefGoogle Scholar
Gudmundsson, K. & Colonius, T. 2011 Instability wave models for the near-field fluctuations of turbulent jets. J. Fluid Mech. 689, 97–128.Google Scholar
Hecht, F. 2011 FreeFem++ manual, 3rd edn, version 3.16-1. Tech. Rep. Available athttp://www.freefem.org/ff++.Google Scholar
Hernandez, V., Roman, J. E. & Vidal, V. 2005 SLEPc: a scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans. Math. Softw. 31 (3), 351–362.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
Jendoubi, S. & Strykowski, P. J. 1994 Absolute and convective instability of axisymmetric jets with external flow. Phys. Fluids 6 (9), 3000.Google Scholar
Lesshafft, L. 2007 Global modes and aerodynamic sound radiation in self-excited hot jets. PhD thesis, Ecole Polytechnique.Google Scholar
Marquet, O. & Sipp, D. 2010 Global sustained perturbations in a backward-facing step flow. In Seventh IUTAM Symposium on Laminar–Turbulent Transition. Springer.Google Scholar
Matsushima, T. & Marcus, P. S. 1995 A spectral method for polar coordinates. J. Comput. Phys. 120, 365–374.Google Scholar
Michalke, A. 1984 Survey on jet instability theory. Prog. Aerosp. Sci. 21, 159–199.Google Scholar
Monkewitz, P. A. 1989 Feedback control of global oscillations in fluid systems. AIAA Paper 89-0991.Google Scholar
Monkewitz, P. A. & Sohn, K. 1988 Absolute instability in hot jets. AIAA J. 26 (8), 911–916.Google Scholar
Monokrousos, A., Akervik, E., Brandt, L. & Henningson, D. S. 2010 Global three-dimensional optimal disturbances in the Blasius boundary-layer flow using time-steppers. J. Fluid Mech. 650, 181.Google Scholar
Moore, C. J. 1977 The role of shear-layer instability waves in jet exhaust noise. J. Fluid Mech. 80 (2), 321.Google Scholar
Nichols, J. W. & Lele, S. K. 2010 Global mode analysis of turbulent high-speed jets. Annual Research Briefs 2010, Center for Turbulence Research.Google Scholar
Nichols, J. W. & Lele, S. K. 2011a Global modes and transient response of a cold supersonic jet. J. Fluid Mech. 669, 225–241.CrossRefGoogle Scholar
Nichols, J. W. & Lele, S. K. 2011b Non-normal global modes of high-speed jets. Intl J. Spray Combust. Dyn. 3 (4), 285–302.CrossRefGoogle Scholar
Pier, B. 2002 On the frequency selection of finite-amplitude vortex shedding in the cylinder wake. J. Fluid Mech. 458.CrossRefGoogle Scholar
Ray, P. K., Cheung, L. C. & Lele, S. K. 2009 On the growth and propagation of linear instability waves in compressible turbulent jets. Phys. Fluids 21 (5), 054106.Google Scholar
Rodriguez Alvarez, D., Samanta, A., Cavalieri, A. V. G., Colonius, T. & Jordan, P. 2011 Parabolized stability equation models for predicting large-scale mixing noise of turbulent round jets. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference, Portland, Oregon. AIAA Paper 2011-2743.Google Scholar
Sipp, D. & Marquet, O. 2012 Characterization of noise amplifiers with global singular modes: the case of the leading-edge flat-plate boundary layer. Theor. Comput. Fluid Dyn., doi:10.1007/s00162-012-0265-y.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.Google Scholar