Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T23:13:52.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Preferential concentration driven instability of sheared gas–solid suspensions

Published online by Cambridge University Press:  30 March 2015

M. Houssem Kasbaoui ,
Donald L. Koch ,
Ganesh Subramanian  and
Olivier Desjardins
M. Houssem Kasbaoui*
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
Donald L. Koch
Affiliation:
School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
Ganesh Subramanian
Affiliation:
Engineering Mechanics, JNCASR, Bangalore 560064, India
Olivier Desjardins
Affiliation:
Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the linear stability of a homogeneous gas–solid suspension of small Stokes number particles, with a moderate mass loading, subject to a simple shear flow. The modulation of the gravitational force exerted on the suspension, due to preferential concentration of particles in regions of low vorticity, in response to an imposed velocity perturbation, can lead to an algebraic instability. Since the fastest growing modes have wavelengths small compared with the characteristic length scale (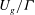$U_{g}/{\it\Gamma}$) and oscillate with frequencies large compared with 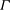${\it\Gamma}$, 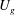$U_{g}$ being the settling velocity and 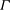${\it\Gamma}$ the shear rate, we apply the WKB method, a multiple scale technique. This analysis reveals the existence of a number density mode which travels due to the settling of the particles and a momentum mode which travels due to the cross-streamline momentum transport caused by settling. These modes are coupled at a turning point which occurs when the wavevector is nearly horizontal and the most amplified perturbations are those in which a momentum wave upstream of the turning point creates a downstream number density wave. The particle number density perturbations reach a finite, but large amplitude that persists after the wave becomes aligned with the velocity gradient. The growth of the amplitude of particle concentration and fluid velocity disturbances is characterised as a function of the wavenumber and Reynolds number (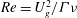$\mathit{Re}=U_{g}^{2}/{\it\Gamma}{\it\nu}$) using both asymptotic theory and a numerical solution of the linearised equations.

JFM classification

Instability: Instability Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Multiphase and Particle-laden Flows: Particle/fluid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 770 , 10 May 2015 , pp. 85 - 123
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfaro, S. C. & Gomez, L. 2001 Modeling mineral aerosol production by wind erosion: emission intensities and aerosol size distributions in source areas. J. Geophys. Res. 106 (D16), 18075–18084.Google Scholar
Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105; WOS:000178731400003.Google Scholar
Anderson, K., Sundaresan, S. & Jackson, R. 1995 Instabilities and the formation of bubbles in fluidized beds. J. Fluid Mech. 303, 327–366.CrossRefGoogle Scholar
Baggett, J. S. & Trefethen, L. N. 1997 Low-dimensional models of subcritical transition to turbulence. Phys. Fluids 9 (4), 1043–1053.CrossRefGoogle Scholar
Batchelor, G. K. 1988 A new theory of the instability of a uniform fluidized bed. J. Fluid Mech. 193, 75–110.CrossRefGoogle Scholar
Batchelor, G. K. & Nitsche, J. M. 1991 Instability of stationary unbounded stratified fluid. J. Fluid Mech. 227, 357–391.Google Scholar
Bellman, R. 1997 Introduction to Matrix Analysis, 2nd edn. Society for Industrial and Applied Mathematics.Google Scholar
Bender, C. M. & Orszag, S. A. 1999 Advanced Mathematical Methods for Scientists and Engineers: Asymptotic Methods and Perturbation Theory. Springer.Google Scholar
Craik, A. D. D. & Criminale, W. O. 1986 Evolution of wavelike disturbances in shear flows: a class of exact solutions of the Navier–Stokes equations. Proc. R. Soc. Lond. A 406 (1830), 13–26.Google Scholar
Dasgupta, S., Jackson, R. & Sundaresan, S. 1994 Turbulent gas–particle flow in vertical risers. AIChE J. 40 (2), 215–228.Google Scholar
Druzhinin, O. A. 1995 On the two-way interaction in two-dimensional particle-laden flows: the accumulation of particles and flow modification. J. Fluid Mech. 297, 49–76.Google Scholar
Dyson, F. J. 1949 The radiation theories of Tomonaga, Schwinger, and Feynman. Phys. Rev. 75 (3), 486–502.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1993 On the two-way interaction between homogeneous turbulence and dispersed solid particles. I: turbulence modification. Phys. Fluids A 5 (7), 1790–1801.Google Scholar
Ferry, J. & Balachandar, S. 2001 A fast Eulerian method for disperse two-phase flow. Intl J. Multiphase Flow 27 (7), 1199–1226.Google Scholar
Ferry, J. & Balachandar, S. 2002 Equilibrium expansion for the Eulerian velocity of small particles. Powder Technol. 125 (23), 131–139.Google Scholar
Gradshteyn, I. S., Ryzhik, I. M., Jeffrey, A. & Zwillinger, D. 2000 Table of Integrals, Series, and Products, 6th edn. Academic.Google Scholar
Hinch, E. J. 1991 Perturbation Methods. Cambridge University Press.Google Scholar
Kelvin, L. 1887 Stability of fluid motion: rectilinear motion of viscous fluid between two parallel plates. Phil. Mag. 24 (5), 188–196.Google Scholar
Lun, C. K. K., Savage, S. B., Jeffrey, D. J. & Chepurniy, N. 1984 Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 140, 223–256.Google Scholar
Magnus, W. 1954 On the exponential solution of differential equations for a linear operator. Commun. Pure Appl. Maths 7 (4), 649–673.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.Google Scholar
Nishimura, K. & Hunt, J. C. R. 2000 Saltation and incipient suspension above a flat particle bed below a turbulent boundary layer. J. Fluid Mech. 417, 77–102.Google Scholar
Parthasarathy, R. N. & Faeth, G. M. 1990 Turbulence modulation in homogeneous dilute particle-laden flows. J. Fluid Mech. 220, 485–514.Google Scholar
Rani, S. L. & Balachandar, S. 2003 Evaluation of the equilibrium Eulerian approach for the evolution of particle concentration in isotropic turbulence. Intl J. Multiphase Flow 29 (12), 1793–1816.Google Scholar
Saffman, P. G. 1962 On the stability of laminar flow of a dusty gas. J. Fluid Mech. 13 (01), 120–128.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39 (1), 129–162.CrossRefGoogle Scholar
Schmid, P. J. & Kytomaa, H. K. 1994 Transient and asymptotic stability of granular shear flow. J. Fluid Mech. 264, 255–275.CrossRefGoogle Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3 (5), 1169–1178.Google Scholar
Tio, K.-K., Gañán-Calvo, A. M. & Lasheras, J. C. 1993 The dynamics of small, heavy, rigid spherical particles in a periodic stuart vortex flow. Phys. Fluids A 5 (7), 1679–1693.Google Scholar
Trefethen, L. 1997 Pseudospectra of linear operators. SIAM Rev. 39 (3), 383–406.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261, 578–584.Google Scholar
Wang, C.-H., Jackson, R. & Sundaresan, S. 1996 Stability of bounded rapid shear flows of a granular material. J. Fluid Mech. 308, 31–62.CrossRefGoogle Scholar
Wang, L.-P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar