Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-08T02:14:50.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Predictions of microstructure and stress in planar extensional flows of a dense viscous suspension

Published online by Cambridge University Press:  11 February 2021

James T. Jenkins Open the ORCID record for James T. Jenkins [Opens in a new window] ,
Ryohei Seto Open the ORCID record for Ryohei Seto [Opens in a new window]  and
Luigi La Ragione Open the ORCID record for Luigi La Ragione [Opens in a new window]
James T. Jenkins*
Affiliation:
School of Civil and Environmental Engineering, Cornell University, Ithaca, NY14853, USA
Ryohei Seto*
Affiliation:
Wenzhou Institute, University of Chinese Academy of Sciences, Wenzhou, Zhejiang325001, PR China
Luigi La Ragione
Affiliation:
Dipartimento di Scienze dell'Ingegneria Civile e dell'Architettura, Politecnico di Bari, 70125Bari, Italy
*
†Email address for correspondence regarding the model: [email protected]
‡Email address for correspondence regarding the simulation: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

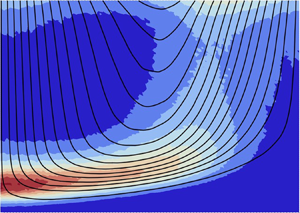
We consider extensional flows of a dense layer of spheres in a viscous fluid and employ force and torque balances to determine the trajectory of particle pairs that contribute to the stress. In doing this, we use Stokesian dynamics simulations to guide the choice of the near-contacting pairs that follow such a trajectory. We specify the boundary conditions on the representative trajectory, and determine the distribution of particles along it and how the stress depends on the microstructure and strain rate. We test the resulting predictions using the numerical simulations. Also, we show that the relation between the tensors of stress and strain rate involves the second and fourth moments of the particle distribution function.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 912 , 10 April 2021 , A27
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Advani, S.G. & Tucker, C.L. 1987 The use of tensors to describe and predict fiber orientation in short fiber composites. J.Rheol. 31, 751–784.CrossRefGoogle Scholar
Advani, S.G. & Tucker, C.L. 1990 Closure approximations for three dimensional structure tensors. J.Rheol. 34, 367–386.CrossRefGoogle Scholar
Ball, R.C. & Melrose, J.R. 1995 Lubrication breakdown in hydrodynamic simulations of concentrated colloids. Adv. Colloid Interface Sci. 59, 19–30.CrossRefGoogle Scholar
Boyer, F., Guazzelli, E. & Pouliquen, O. 2011 Unifying suspension and granular rheology. Phys. Rev. Lett. 107, 188301.CrossRefGoogle ScholarPubMed
Brady, J.F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20 (1), 111–157.CrossRefGoogle Scholar
Chacko, R.N., Mari, R., Fielding, S.M. & Cates, M.E. 2018 Shear reversal in dense suspensions: the challenge to fabric evolution models from simulation data. J.Fluid Mech. 847, 700–734.CrossRefGoogle Scholar
Gillissen, J.J.J. & Wilson, H.J. 2018 Modeling sphere suspension microstructure and stress. Phys. Rev. E 98, 033119.CrossRefGoogle Scholar
Gillissen, J.J.J. & Wilson, H.J. 2019 The effect of normal contact forces on the stress in shear rate invariant particle suspensions. Phys. Rev. Fluids 4, 013301.CrossRefGoogle Scholar
Gillissen, J.J.J., Ness, C., Peterson, J.D., Wilson, H.J. & Cates, M.E. 2019 Constitute models for time-dependent flows. Phys. Rev. Lett. 123, 214504.CrossRefGoogle Scholar
Goddard, J.D. 2006 A dissipative anisotropic fluid model for non-colloidal particle suspensions. J.Fluid Mech. 568, 1–17.CrossRefGoogle Scholar
Guazzelli, E. & Pouliquen, O. 2018 Rheology of dense granular suspensions. J.Fluid Mech. 852, P1.CrossRefGoogle Scholar
Jeffrey, D.J. 1992 The calculation of low Reynolds number resistance functions for two unequal spheres. Phys. Fluids A 4, 16–29.CrossRefGoogle Scholar
Jeffrey, D.J. & Onishi, Y. 1984 Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J.Fluid Mech. 139, 261–290.CrossRefGoogle Scholar
Jenkins, J.T., La Ragione, L., Johnson, D. & Makse, H.A. 2005 Fluctuations and effective moduli of an isotropic, random aggregate of identical, frictionless spheres. J.Mech. Phys. Solids 53, 197–225.CrossRefGoogle Scholar
Jenkins, J.T. & La Ragione, L. 2015 An analytical determination of microstructure and stresses in a dense, sheared monolayer of non-Brownian spheres. J.Fluid Mech. 763, 218–236.CrossRefGoogle Scholar
Kraynik, A.M. & Reinelt, D.A. 1992 Extensional motions of spatially periodic lattices. Intl J. Multiphase Flow 18, 1045–1059.CrossRefGoogle Scholar
Love, A.E.H. 1944 A Treatise on the Mathematical Theory of Elasticity, 3rd edn. Cambridge University Press.Google Scholar
Mari, R., Seto, R., Morris, J.F. & Denn, M.M. 2014 Shear thickening, frictionless and frictional rheologies in non-Brownian suspensions. J.Rheol. 58, 1693–1724.CrossRefGoogle Scholar
Nazockdast, E. & Morris, J.F. 2012 a Microstructural theory and rheology of concentrated suspensions. J.Fluid Mech. 713, 420–452.CrossRefGoogle Scholar
Nazockdast, E. & Morris, J.F. 2012 b Effect of repulsive interaction on structure and rheology of sheared colloidal suspensions. Soft Matt. 8, 4223–4234.CrossRefGoogle Scholar
Nazockdast, E. & Morris, J.F. 2013 Pair-particle dynamics and microstructure in sheared colloidal suspensions: simulation and Smoluchowski theory. Phys. Fluids 25, 25070601.CrossRefGoogle Scholar
Nott, P.R. & Brady, J.F. 1994 Pressure-driven flow of suspensions: simulation and theory. J.Fluid Mech. 275, 157–199.CrossRefGoogle Scholar
Onat, E.T. & Leckie, F.A. 1988 Representation of mechanical behavior in the presence of changing internal structure. Trans. ASME: J. Appl. Mech. 55, 1–10.CrossRefGoogle Scholar
Phan-Thien, N. 1995 Constitutive relation for concentrated suspensions in Newtonian liquids. J.Rheol. 39, 679–695.CrossRefGoogle Scholar
Prantil, V.C., Jenkins, J.T. & Dawson, P.R. 1993 An analysis of texture and plastic spin for planar polycristal. J.Mech. Phys. Solids 41, 1357–1382.CrossRefGoogle Scholar
Seto, R., Giusteri, G.G. & Martiniello, A. 2017 Microstructure and thickening of dense suspensions under extensional and shear flows. J.Fluid Mech. 825, R3.CrossRefGoogle Scholar
Singh, A. & Nott, P.R. 2000 Normal stresses and microstructure in bounded sheared suspensions via Stokesian dynamics simulations. J.Fluid Mech. 412, 279–301.CrossRefGoogle Scholar
Stickel, J.J., Phillips, R.J. & Powell, R.L. 2006 A constitutive model for microstructure and total stress in particulate suspensions. J.Rheol. 50, 379–413.CrossRefGoogle Scholar
Thomas, J.E., Ramola, K., Singh, A., Mari, R., Morris, J.F. & Chakraborty, B. 2018 Microscopic origin of frictional rheology in dense suspensions: correlations in force space. Phys. Rev. Lett. 121, 128002.CrossRefGoogle ScholarPubMed
Todd, B.D. & Daivis, P.J. 1998 Nonequilibrium molecular dynamics simulations of planar elongational flow with spatially and temporally periodic boundary conditions. Phys. Rev. Lett. 81, 1118–1121.CrossRefGoogle Scholar
Torquato, S. 1995 Nearest-neighbor statistics for packings of hard spheres and disks. Phys. Rev. E 51, 3170–3184.CrossRefGoogle ScholarPubMed