Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T04:47:14.013Z Has data issue: false hasContentIssue false
  • English
  • Français

Precursors of backflow events and their relationship with the near-wall self-sustaining process

Published online by Cambridge University Press:  29 December 2021

Byron Guerrero Open the ORCID record for Byron Guerrero [Opens in a new window] ,
Martin F. Lambert Open the ORCID record for Martin F. Lambert [Opens in a new window]  and
Rey C. Chin Open the ORCID record for Rey C. Chin [Opens in a new window]
Byron Guerrero*
Affiliation:
School of Mechanical Engineering, University of Adelaide, Adelaide, South Australia5005
Martin F. Lambert
Affiliation:
School of Civil, Environmental & Mining Engineering, University of Adelaide, Adelaide, South Australia5005
Rey C. Chin
Affiliation:
School of Mechanical Engineering, University of Adelaide, Adelaide, South Australia5005
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

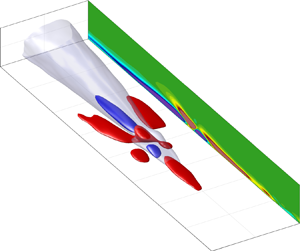
This study examines the precursors and consequences of rare backflow events at the wall using direct numerical simulation of turbulent pipe flow with a high spatiotemporal resolution. The results obtained from conditionally averaged fields reveal that the precursor of a backflow event is the asymmetric collision between a high- and a low-speed streak (LSS) associated with the sinuous mode of the streaks. As the collision occurs, a lifted shear layer with high local azimuthal enstrophy is formed at the trailing end of the LSS. Subsequently, a spanwise or an oblique vortex spontaneously arises. The dominant nonlinear mechanism by which this vortex is engendered is enstrophy intensification due to direct stretching of the lifted vorticity lines in the azimuthal direction. As time progresses, this vortex tilts and orientates towards the streamwise direction and, as its enstrophy increases, it induces the breakdown of the LSS located below it. Subsequently, this vortical structure advects as a quasi-streamwise vortex, as it tilts and stretches with time. As a result, it is shown that reverse flow events at the wall are the signature of the nonlinear mechanism of the self-sustaining process occurring at the near-wall region. Additionally, each backflow event has been tracked in space and time, showing that approximately 50 % of these events are followed by at least one additional vortex generation that gives rise to new backflow events. It is also found that up to a maximum of seven regenerations occur after a backflow event has appeared for the first time.

JFM classification

Turbulent Flows: Intermittency Turbulent Flows: Turbulence simulation Turbulent Flows: Pipe flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 933 , 25 February 2022 , A33
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adrian, R.J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
Adrian, R., Meinhart, C. & Tomkins, C. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Avila, M., Mellibovsky, F., Roland, N. & Hof, B. 2013 Streamwise-localized solutions at the onset of turbulence in pipe flow. Phys. Rev. Lett. 110, 224502.CrossRefGoogle Scholar
Bae, H., Lozano-Durán, A. & McKeon, B. 2021 Non-linear mechanism of the self-sustaining process in the buffer and logarithmic layer of wall-bounded flows. J. Fluid Mech. 914, A3.CrossRefGoogle Scholar
Batchelor, G.K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Blackburn, H.M. & Sherwin, S.J. 2004 Formulation of a Galerkin spectral element–Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.CrossRefGoogle Scholar
Blonigan, P.J., Farazmand, M. & Sapsis, T.P. 2019 Are extreme dissipation events predictable in turbulent fluid flows? Phys. Rev. Fluids 4, 044606.CrossRefGoogle Scholar
Brandt, L. & de Lange, H. 2008 Streak interactions and breakdown in boundary layer flows. Phys. Fluids 20, 024107.CrossRefGoogle Scholar
Brandt, L., Schlatter, P. & Henningson, D. 2004 Transition in boundary layers subject to free-stream turbulence. J. Fluid Mech. 517, 167–198.CrossRefGoogle Scholar
Bross, M., Fuchs, T. & Kähler, C. 2019 Interaction of coherent flow structures in adverse pressure gradient turbulent boundary layers. J. Fluid Mech. 873, 287–321.CrossRefGoogle Scholar
Brücker, C. 2015 Evidence of rare backflow and skin-friction critical points in near-wall turbulence using micropillar imaging. Phys. Fluids 27, 031705.CrossRefGoogle Scholar
Cardesa, J.I., Monty, J.P., Soria, J. & Chong, M.S. 2014 Skin-friction critical points in wall-bounded flows. J. Phys.: Conf. Ser. 506, 012009.Google Scholar
Cardesa, J.I., Monty, J.P., Soria, J. & Chong, M.S. 2019 The structure and dynamics of backflow in turbulent channels. J. Fluid Mech. 880, R3.CrossRefGoogle Scholar
Chin, R.C., Monty, J.P., Chong, M.S. & Marusic, I. 2018 Conditionally averaged flow topology about a critical point pair in the skin friction field of pipe flows using direct numerical simulations. Phys. Rev. Fluids 3, 114607.CrossRefGoogle Scholar
Chin, C., Ooi, A.S.H., Marusic, I. & Blackburn, H.M. 2010 The influence of pipe length on turbulence statistics computed from direct numerical simulation data. Phys. Fluids 22, 115107.CrossRefGoogle Scholar
Chin, C., Philip, J., Klewicki, J., Ooi, A. & Marusic, I. 2014 Reynolds-number-dependent turbulent inertia and onset of log region in turbulent pipe flows. J. Fluid Mech. 757, 747–769.CrossRefGoogle Scholar
Chin, R.C., Vinuesa, R., Örlü, R., Cardesa, J.I., Noorani, A., Chong, M.S. & Schlatter, P. 2020 Backflow events under the effect of secondary flow of Prandtl's first kind. Phys. Rev. Fluids 5, 074606.CrossRefGoogle Scholar
Davidson, P.A. 2004 Turbulence an Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Diaz-Daniel, C., Laizet, S. & Vassilicos, J.C. 2017 Wall shear stress fluctuations: mixed scaling and their effects on velocity fluctuations in a turbulent boundary layer. Phys. Fluids 29, 055102.CrossRefGoogle Scholar
Eckelmann, H. 1974 The structure of the viscous sublayer and the adjacent wall region in a turbulent channel flow. J. Fluid Mech. 65, 439–459.CrossRefGoogle Scholar
Eitel-Amor, G., Örlü, R., Schlatter, P. & Flores, O. 2015 Hairpin vortices in turbulent boundary layers. Phys. Fluids 27 (2), 025108.CrossRefGoogle Scholar
Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91, 224502.CrossRefGoogle ScholarPubMed
Farano, M., Cherubini, S., De Palma, P. & Robinet, J. 2018 Nonlinear optimal large-scale structures in turbulent channel flow. Eur. J. Mech. B/Fluids 72, 74–86.CrossRefGoogle Scholar
Farano, M., Cherubini, S., Robinet, J. & De Palma, P. 2017 Optimal bursts in turbulent channel flow. J. Fluid Mech. 817, 35–60.CrossRefGoogle Scholar
Farazmand, M. & Sapsis, T.P. 2017 A variational approach to probing exteme events in turbulent dynamical systems. Sci. Adv. 3, e1701533.CrossRefGoogle Scholar
Gomit, G., De Kat, R. & Ganapathisubramani, B. 2018 Structure of high and low-shear stress events in a turbulent boundary layer. Phys. Rev. Fluids 3, 014609.CrossRefGoogle Scholar
Goudar, M., Breugem, W. & Elsinga, G. 2016 Auto-generation in wall turbulence by the interaction of weak eddies. Phys. Fluids 28, 035111.CrossRefGoogle Scholar
Guerrero, B., Lambert, M.F. & Chin, R.C. 2020 Extreme wall shear stress events in turbulent pipe flows: spatial characteristics of coherent motions. J. Fluid Mech. 904, A18.CrossRefGoogle Scholar
Hack, M.J.P. & Schmidt, O.T. 2021 Extreme events in wall turbulence. J. Fluid Mech. 907, A9.CrossRefGoogle Scholar
Hamilton, J., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.CrossRefGoogle Scholar
Head, M.R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.CrossRefGoogle Scholar
Heist, D. & Hanratty, T. 2000 Observations of the formation of streamwise vortices by rotation of arch vortices. Phys. Fluids 12, 2965–2975.CrossRefGoogle Scholar
Hof, B., van Doorne, C., Westerweel, J., Nieuwstadt, F., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. & Waleffe, F. 2004 Experimental observation of nonlinear traveling waves in turbulent pipe flow. Science 305 (5690), 1594–1598.CrossRefGoogle ScholarPubMed
Hunt, J., Wray, A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Proc. of the summer program 1988, pp. 193–208. Center for Turbulence Research.Google Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. 365, 647–664.CrossRefGoogle ScholarPubMed
Hutchins, N., Monty, J.P., Ganapathisubramani, B., Ng, H.C.H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.CrossRefGoogle Scholar
Jalalabadi, R. & Sung, H. 2018 Influence of backflow on skin friction in turbulent pipe flow. Phys. Fluids 30, 065104.CrossRefGoogle Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.CrossRefGoogle Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44 (1), 203–225.CrossRefGoogle Scholar
Kim, H., Kline, S. & Reynolds, W. 1971 The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50, 133–160.CrossRefGoogle Scholar
Kline, S.J., Reynolds, W.C., Schraub, F.A. & Runstadler, P.W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (4), 741–773.CrossRefGoogle Scholar
Landahl, M.T. & Mollo-Christensen, E. 1992 Turbulence and Random Processes in Fluid Mechanics. Cambridge University Press.CrossRefGoogle Scholar
Lee, J., Hutchis, N. & Monty, J. 2019 Formation and evolution of shear layers in a developing turbulent boundary layer. In 11th International Symposium on Turbulence and Shear Flow Phenomena. Southampton, UK.Google Scholar
Lenaers, P., Li, Q., Brethouwer, G., Schlatter, P. & Örlü, R. 2012 Rare backflow and extreme wall-normal velocity fluctuations in near-wall turbulence. Phys. Fluids 24, 035110.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329, 193–196.CrossRefGoogle ScholarPubMed
McKeon, B.J. 2017 The engine behind (wall) turbulence: perspectives on scale interactions. J. Fluid Mech. 817, P1.CrossRefGoogle Scholar
Meinhart, C. & Adrian, R. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7, 694–696.CrossRefGoogle Scholar
Morton, B.R. 1984 The generation and decay of vorticity. Geophys. Astrophys. Fluid Dyn. 28, 277–308.CrossRefGoogle Scholar
Pan, C. & Kwon, Y. 2018 Extremely high wall-shear stress events in a turbulent boundary layer. J. Phys.: Conf. Ser. 1001, 012004.Google Scholar
Panton, R. 1999 Self-sustaining mechanisms of wall turbulence - a review. In 37th Aerospace Sciences Meeting and Exhibit, AIAA Paper 99-0552.Google Scholar
Panton, R. 2001 Overview of the self-sustaining mechanisms of wall turbulence. Prog. Aerosp. Sci. 37 (4), 341–383.CrossRefGoogle Scholar
Perry, A.E. & Chong, M.S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Örlü, R. & Schlatter, P. 2011 On the fluctuating wall-shear stress in zero pressure-gradient turbulent boundary layer flows. Phys. Fluids 23, 021704.CrossRefGoogle Scholar
Örlü, R. & Vinuesa, R. 2020 Instantaneous wall-shear-stress measurements: advances and application to near-wall extreme events. Meas. Sci. Technol. 31 (11), 112001.CrossRefGoogle Scholar
Robinson, S.K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.CrossRefGoogle Scholar
Schlatter, P., Brandt, L., de Lange, H. & Henningson, D. 2008 On streak breakdown in bypass transition. Phys. Fluids 20, 101505.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 1997 Genesis and Dynamics of Coherent Structures in Near-Wall Turbulence: A New Look. Computational Mechanics Inc.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–106.CrossRefGoogle Scholar
Sheng, J., Malkiel, E. & Katz, J. 2009 Buffer layer structures associated with extreme wall stress events in a smooth wall turbulent boundary layer. J. Fluid Mech. 633, 17–60.CrossRefGoogle Scholar
de Silva, C., Hutchins, N. & Marusic, I. 2016 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.CrossRefGoogle Scholar
Smith, C.R., Walker, J.D.A., Haidari, A.H., Sobrun, U., Walker, J.D.A. & Smith, F.T. 1991 On the dynamics of near-wall turbulence. Phil. Trans. R. Soc. Lond. A 336 (1641), 131–175.Google Scholar
Tong, T., Bhatt, K., Tsuneyoshi, T. & Tsuji, Y. 2020 Effect of large-scale structures on wall shear stress fluctuations in pipe flow. Phys. Rev. Fluids 5, 104601.CrossRefGoogle Scholar
Vinuesa, R., Örlü, R. & Schlatter, P. 2017 Characterisation of backflow events over a wing section. J. Turbul. 18 (2), 170–185.CrossRefGoogle Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9 (4), 883–900.CrossRefGoogle Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81, 4140–4143.CrossRefGoogle Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.CrossRefGoogle Scholar
Waleffe, F. 2009 Exact coherent structures in turbulent shear flows. In Notes on Numerical Fluid Mechanics and Multidisciplinary Design. Springer.CrossRefGoogle Scholar
Willert, C.E., et al. 2018 Experimental evidence of near-wall reverse flow events in zero pressure gradient turbulent boundary layers. Exp. Therm. Fluid Sci. 91, 320–328.CrossRefGoogle Scholar
Wu, X., Cruickshank, M. & Ghaemi, S. 2020 Negative skin friction during transition in a zero-pressure-gradient flat-plate boundary layer and in pipe flows with slip and no-slip boundary conditions. J. Fluid Mech. 887, 1–35.CrossRefGoogle Scholar
Zhou, J., Adrian, R., Balachandar, S. & Kendall, T. 1998 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 225, 353–396.Google Scholar