Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T16:34:23.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Potential enstrophy in stratified turbulence

Published online by Cambridge University Press:  09 April 2013

Michael L. Waite
Michael L. Waite*
Affiliation:
Department of Applied Mathematics, University of Waterloo, 200 University Avenue W., Waterloo, ON N2L 3G1, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

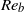Direct numerical simulations are used to investigate potential enstrophy in stratified turbulence with small Froude numbers, large Reynolds numbers, and buoyancy Reynolds numbers ($R{e}_{b} $) both smaller and larger than unity. We investigate the conditions under which the potential enstrophy, which is a quartic quantity in the flow variables, can be approximated by its quadratic terms, as is often done in geophysical fluid dynamics. We show that at large scales, the quadratic fraction of the potential enstrophy is determined by 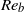$R{e}_{b} $. The quadratic part dominates for small 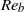$R{e}_{b} $, i.e. in the viscously coupled regime of stratified turbulence, but not when $R{e}_{b} \gtrsim 1$. The breakdown of the quadratic approximation is consistent with the development of Kelvin–Helmholtz instabilities, which are frequently observed to grow on the layerwise structure of stratified turbulence when 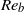$R{e}_{b} $ is not too small.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulence simulation
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 722 , 10 May 2013 , R4
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almalkie, S. & deBruynKops, S. M. 2012 Kinetic energy dynamics in forced, horizontally homogeneous and isotropic, stably stratified turbulence. J. Turbul. 13, N29.Google Scholar
Aluie, H. & Kurien, S. 2011 Joint downscale fluxes of energy and potential enstrophy in rotating stratified Boussinesq flows. Eur. Phys. Lett. 96, 44006.Google Scholar
Augier, P., Chomaz, J.-M. & Billant, P. 2012 Spectral analysis of the transition to turbulence from a dipole in stratified fluids. J. Fluid Mech. 713, 167–188.Google Scholar
Bartello, P. 1995 Geostrophic adjustment and inverse cascades in rotating stratified turbulence. J. Atmos. Sci. 52, 4410–4428.Google Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13, 1645–1651.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Charney, J. G. 1971 Geostrophic turbulence. J. Atmos. Sci. 28, 1087–1095.Google Scholar
Dewan, E. M. 1997 Saturated-cascade similitude theory of gravity wave spectra. J. Geophys. Res. 102, 29799–29817.Google Scholar
Fjørtoft, R. 1953 On the changes in the spectral distribution of kinetic energy for two-dimensional non-divergent flow. Tellus 5, 225–230.Google Scholar
Godoy-Diana, R., Chomaz, J.-M. & Billant, P. 2004 Vertical length scale selection for pancake vortices in strongly stratified viscous fluids. J. Fluid Mech. 504, 229–238.Google Scholar
Hebert, D. A. & deBruynKops, S. M. 2006 Relationship between vertical shear rate and kinetic energy dissipation rate in stably stratified flows. Geophys. Res. Lett. 33, L06602.Google Scholar
Herring, J. R., Kerr, R. M. & Rotunno, R. 1994 Ertel’s potential vorticity in unstratified turbulence. J. Atmos. Sci. 51, 35–47.Google Scholar
Kimura, Y. & Herring, J. R. 2012 Energy spectra of stably stratified turbulence. J. Fluid Mech. 698, 19–50.CrossRefGoogle Scholar
Kurien, S., Smith, L. & Wingate, B. 2006 On the two-point correlation of potential vorticity in rotating and stratified turbulence. J. Fluid Mech. 555, 131–140.Google Scholar
Laval, J.-P., McWilliams, J. C. & Dubrulle, B. 2003 Forced stratified turbulence: Successive transitions with Reynolds number. Phys. Rev. E 68, 036308.Google Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
Moum, J. N. 1996 Energy-containing scales of turbulence in the ocean thermocline. J. Geophys. Res. 101, 14095–14109.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.Google Scholar
Praud, O., Fincham, A. M. & Sommeria, J. 2005 Decaying grid turbulence in a strongly stratified fluid. J. Fluid Mech. 522, 1–33.Google Scholar
Riley, J. J. & deBruynKops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15, 2047–2059.Google Scholar
Riley, J. J. & Lelong, M.-P. 2000 Fluid motions in the presence of strong stable stratification. Annu. Rev. Fluid Mech. 32, 613–657.Google Scholar
Smith, L. M. & Waleffe, F. 2002 Generation of slow large-scales in forced rotating stratified turbulence. J. Fluid Mech. 451, 145–168.Google Scholar
Waite, M. L. 2011 Stratified turbulence at the buoyancy scale. Phys. Fluids 23, 066602.Google Scholar
Waite, M. L. 2013 Direct numerical simulations of laboratory-scale stratified turbulence. In Modelling Atmospheric and Oceanic Flows: Insights from Laboratory Experiments (ed. von Larcher, T. & Williams, P. D.). American Geophysical Union (in press).Google Scholar
Waite, M. L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–308.Google Scholar
Waite, M. L. & Bartello, P. 2006 The transition from geostrophic to stratified turbulence. J. Fluid Mech. 568, 89–108.Google Scholar