Article contents
Post-stall flow control on aerofoils by leading-edge flags
Published online by Cambridge University Press: 26 September 2023
Abstract
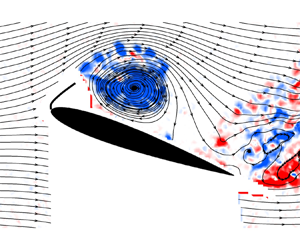
Self-excited oscillations of flags attached at the leading edge of aerofoils have been investigated at post-stall angles of attack at a chord Reynolds number of 100 000. Significant increases in the time-averaged lift coefficient and stall angle have been observed for three aerofoils: one symmetric, one cambered and one with a sharp leading edge. The aerodynamic improvement is due to the periodic formation of vortices caused by the flag oscillations. When the flag is near the aerofoil surface, it is lifted upwards by the induced velocity of the growing vortex. As the flag moves up, the vortex grows in strength and reaches maximum circulation when the flag is furthest from the aerofoil surface and subsequently sheds. Flags with large stiffness exhibit better spatial and temporal coherence of flag oscillations than the compliant flags, resulting in a larger maximum lift coefficient and higher stall angle. For all aerofoils tested, the best lift enhancement with respect to the clean aerofoils is found when the angle of attack is 6° to 10° above the stall angle of the clean aerofoil. High lift is observed when the flags are locked in with the wake instability in a narrow frequency band, depending on the flag mass ratio and length.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 6
- Cited by



