Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-27T23:44:44.877Z Has data issue: false hasContentIssue false
  • English
  • Français

Polymer scission in turbulent flows

Published online by Cambridge University Press:  10 February 2021

Dario Vincenzi Open the ORCID record for Dario Vincenzi [Opens in a new window] ,
Takeshi Watanabe Open the ORCID record for Takeshi Watanabe [Opens in a new window] ,
Samriddhi Sankar Ray Open the ORCID record for Samriddhi Sankar Ray [Opens in a new window]  and
Jason R. Picardo Open the ORCID record for Jason R. Picardo [Opens in a new window]
Dario Vincenzi*
Affiliation:
Université Côte d'Azur, CNRS, LJAD, 06100Nice, France
Takeshi Watanabe
Affiliation:
Department of Physical Science and Engineering, Nagoya Institute of Technology, Gokiso, Nagoya466-8555, Japan
Samriddhi Sankar Ray
Affiliation:
International Centre for Theoretical Sciences, Tata Institute of Fundamental Research, Bangalore560089, India
Jason R. Picardo
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology Bombay, Mumbai400076, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

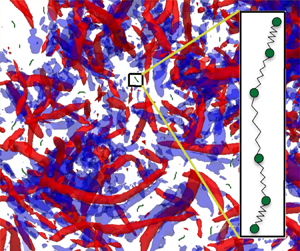
Polymers in a turbulent flow are subject to intense strain, which can cause their scission and thereby limit the experimental study and application of phenomena such as turbulent drag reduction and elastic turbulence. In this paper, we study polymer scission in homogeneous isotropic turbulence, through a combination of stochastic modelling, based on a Gaussian time-decorrelated random flow, and direct numerical simulations (DNS) with both one-way (passive) and two-way (active) coupling of the polymers, modelled as bead-spring chains, and the flow. For the first scission of passive polymers, the stochastic model yields analytical predictions which are found to be in good agreement with results from the DNS, for the temporal evolution of the fraction of unbroken polymers and the statistics of the survival of polymers. The impact of scission on the dynamics of a turbulent polymer solution is investigated through DNS with two-way coupling (active polymers). Our results indicate that the reduction of kinetic energy dissipation due to feedback from stretched polymers is an inherently transient effect, which is lost as the polymers break up. Thus, the overall dissipation reduction is maximized by an intermediate polymer relaxation time, for which polymers stretch significantly but without breaking too quickly. We also study the dynamics of the polymer fragments which form after scission; these daughter polymers can themselves undergo subsequent, repeated, breakups to produce a hierarchical population of polymers with a range of relaxation times and scission rates.

JFM classification

Non-Newtonian Flows: Polymers Turbulent Flows: Isotropic turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 912 , 10 April 2021 , A18
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Allende, S., Henry, C. & Bec, J. 2020 Dynamics and fragmentation of small inextensible fibers in turbulence. Phil. Trans. R. Soc. Lond. A 378, 20190398.Google Scholar
Balkovsky, E., Fouxon, A. & Lebedev, V. 2000 Turbulent dynamics of polymer solutions. Phys. Rev. Lett. 84, 4765–4768.CrossRefGoogle ScholarPubMed
Bec, J., Biferale, L., Boffetta, G., Cencini, M., Lanotte, A., Musacchio, S. & Toschi, F. 2006 Lyapunov exponents of heavy particles in turbulence. Phys. Fluids 18, 091702.CrossRefGoogle Scholar
Benzi, R. 2010 A short review on drag reduction by polymers in wall bounded turbulence. Physica D 239, 1338–1345.CrossRefGoogle Scholar
Biferale, L., Meneveau, C. & Verzicco, R. 2014 Deformation statistics of sub-Kolmogorov-scale ellipsoidal neutrally buoyant drops in isotropic turbulence. J. Fluid Mech. 754, 184–207.CrossRefGoogle Scholar
Bird, R.B., Curtiss, C.F., Armstrong, R.C. & Hassager, O. 1977 Dynamics of Polymeric Liquids, vol. II. Wiley.Google Scholar
Bird, R.B., Dotson, P.J. & Johnson, N.L. 1980 Polymer solution rheology based on a finitely extensible bead–spring chain model. J. Non-Newtonian Fluid Mech. 7, 213–235.CrossRefGoogle Scholar
Cascales, J.J.L. & de la Torre, J.G. 1991 Simulation of polymer chains in elongational flow. Steady-state properties and chain fracture. J. Chem. Phys. 95, 9384–9392.CrossRefGoogle Scholar
Cascales, J.J.L. & de la Torre, J.G., 1992 Simulation of polymer chains in elongational flow. Kinetics of chain fracture and fragment distribution. J. Chem. Phys. 97, 4549–4554.CrossRefGoogle Scholar
Celani, A., Musacchio, S. & Vincenzi, D. 2005 Polymer transport in random flow. J. Stat. Phys. 118, 531–554.CrossRefGoogle Scholar
de Chaumont Quitry, A. & Ouellette, N.T. 2016 Concentration effects on turbulence in dilute polymer solutions far from walls. Phys. Rev. E 93, 063116.CrossRefGoogle ScholarPubMed
Chertkov, M. 2000 Polymer stretching by turbulence. Phys. Rev. Lett. 84, 4761–4764.CrossRefGoogle ScholarPubMed
Choi, H.J., Lim, S.T., Lai, P.-Y. & Chan, C.K., 2002 Turbulent drag reduction and degradation of DNA. Phys. Rev. Lett. 89, 088302.CrossRefGoogle ScholarPubMed
Cifre, J.G.H. & de la Torre, J.G. 1999 Steady-state behavior of dilute polymers in elongational flow. Dependence of the critical elongational rate on chain length, hydrodynamic interaction, and excluded volume. J. Rheol. 43, 339.CrossRefGoogle Scholar
Crawford, A.M., Mordant, N., Xu, H. & Bodenschatz, E. 2008 Fluid acceleration in the bulk turbulence of dilute polymer solutions. New J. Phys. 10, 123015.CrossRefGoogle Scholar
De Angelis, E., Casciola, C.M., Benzi, R. & Piva, R. 2005 Homogeneous isotropic turbulence in dilute polymers. J. Fluid Mech. 531, 1–10.CrossRefGoogle Scholar
Elbing, B.R., Winkel, S., Solomon, J. & Ceccio, L. 2009 Degradation of homogeneous polymer solutions in high shear turbulent pipe flow. Exp. Fluids 47, 1033–1044.CrossRefGoogle Scholar
Falkovich, G., Gawȩdzki, K. & Vergassola, M. 2001 Particles and fields in fluid turbulence. Rev. Mod. Phys. 73, 913–975.CrossRefGoogle Scholar
Girimaji, S.S. & Pope, S.B. 1990 A diffusion model for velocity gradients in turbulence. Phys. Fluids A 2, 242–256.CrossRefGoogle Scholar
Graham, M.D. 2014 Drag reduction and the dynamics of turbulence in simple and complex fluids. Phys. Fluids 26, 101301.CrossRefGoogle Scholar
Groisman, A. & Steinberg, V. 2004 Elastic turbulence in curvilinear flows of polymer solutions. New J. Phys. 6, 29.CrossRefGoogle Scholar
Horn, A.F. & Merrill, E.W. 1984 Midpoint scission of macromolecules in dilute solution in turbulent flow. Nature 312, 140–141.CrossRefGoogle Scholar
Hsieh, C.C., Park, S.J. & Larson, R.G. 2005 Brownian Dynamics modeling of flow-induced birefringence and chain scission in dilute polymer solutions in a planar cross-slot flow. Macromolecules 38, 1456–1468.CrossRefGoogle Scholar
Jendrejack, R.M., de Pablo, J.J. & Graham, M.D. 2002 Stochastic simulations of DNA in flow: dynamics and the effects of hydrodynamic interactions. J. Chem. Phys. 116, 7752.CrossRefGoogle Scholar
Jin, S. & Collins, L.R. 2008 Dynamics of dissolved polymer chains in isotropic turbulence. New J. Phys. 9, 360.CrossRefGoogle Scholar
Kalelkar, C., Govindarajan, R. & Pandit, R. 2005 Drag reduction by polymer additives in decaying turbulence. Phys. Rev. E 72, 017301.CrossRefGoogle ScholarPubMed
Knudsen, K.D., Hernández Cifre, J.G. & García de la Torre, J. 1996 Conformation and fracture of polystyrene chains in extensional flow studied by numerical simulation. Macromolecules 29, 3603–3610.CrossRefGoogle Scholar
Kraichnan, R.H. 1968 Small-scale structure of a scalar field convected by turbulence. Phys. Fluids 11, 945–953.CrossRefGoogle Scholar
Larson, R.G. 1999 The Structure and Rheology of Complex Fluids. Oxford University.Google Scholar
Liu, Y. & Steinberg, V. 2014 Single polymer dynamics in a random flow. Macromol. Symp. 337, 34–43.CrossRefGoogle Scholar
Lumley, J.L. 1972 On the solution of equations describing small scale deformation. In Symposia Mathematica, Istituto Nazionale di Alta Matematica, Bologna, vol. IX, pp. 315–334. Academic Press.Google Scholar
Moussa, T., Tiu, C. & Sridhar, T. 1993 Effect of solvent on polymer degradation in turbulent flow. J. Non-Newtonian Fluid Mech. 48, 261–284.CrossRefGoogle Scholar
Musacchio, S. & Vincenzi, D. 2011 Deformation of a flexible polymer in a random flow with long correlation time. J. Fluid Mech. 670, 326–336.CrossRefGoogle Scholar
Oldroyd, D.J. 1950 On the formulation of rheological equations of state. Proc. R. Soc. Lond. A 200, 523–541.Google Scholar
Öttinger, H.C. 1996 Stochastic Processes in Polymeric Fluids. Springer.CrossRefGoogle Scholar
Ouellette, N.T., Xu, H. & Bodenschatz, E. 2009 Bulk turbulence in dilute polymer solutions. J. Fluid Mech. 629, 375–385.CrossRefGoogle Scholar
Owolabi, B.E., Dennis, D.J.C. & Poole, R.J. 2017 Turbulent drag reduction by polymer additives in parallel-shear flows. J. Fluid Mech. 827, R4.CrossRefGoogle Scholar
Paterson, R.W. & Abernathy, F.H. 1970 Turbulent flow drag reduction and degradation with dilute polymer solutions. J. Fluid Mech. 43, 689–710.CrossRefGoogle Scholar
Pereira, A.S. & Soares, E.J. 2012 Polymer degradation of dilute solutions in turbulent drag reducing flows in a cylindrical double gap rheometer device. J. Non-Newtonian Fluid Mech. 179-180, 9–22.CrossRefGoogle Scholar
Pereira, A.S., Mompean, G. & Soares, E.J. 2018 Modeling and numerical simulations of polymer degradation in a drag reducing plane Couette flow. J. Non-Newtonian Fluid Mech. 256, 1–7.CrossRefGoogle Scholar
Perkins, T.T., Smith, D.E. & Chu, S. 1997 Single polymer dynamics in an elongational flow. Science 276, 2016–2021.CrossRefGoogle Scholar
Perlekar, P., Mitra, D. & Pandit, R. 2006 Manifestations of drag reduction by polymer additives in decaying, homogeneous, isotropic turbulence. Phys. Rev. Lett. 97, 264501.CrossRefGoogle ScholarPubMed
Perlekar, P., Mitra, D. & Pandit, R. 2010 Direct numerical simulations of statistically steady, homogeneous, isotropic fluid turbulence with polymer additives. Phys. Rev. E 82, 066313.CrossRefGoogle ScholarPubMed
Plan, E.L.C.VI.M., Ali, A. & Vincenzi, D. 2016 Bead-rod-spring models in random flows. Phys. Rev. E 94, 020501(R).Google ScholarPubMed
Poole, R.J. 2020 Editorial for the special issue on ‘Polymer degradation in turbulent drag reduction’. J. Non-Newtonian Fluid Mech. 281, 104283.CrossRefGoogle Scholar
Procaccia, I., L'Vov, V.S. & Benzi, R. 2008 Theory of drag reduction by polymers in wall-bounded turbulence. Rev. Mod. Phys. 80, 225–247.CrossRefGoogle Scholar
Ray, S.S. & Vincenzi, D. 2018 Droplets in isotropic turbulence: deformation and breakup statistics. J. Fluid Mech. 852, 313–328.CrossRefGoogle Scholar
Rouse, P.E. 1953 A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 21, 1272–1280.CrossRefGoogle Scholar
Schroeder, C.M., Shaqfeh, E.S.G. & Chu, S. 2004 Effect of hydrodynamic interactions on DNA dynamics in extensional flow: simulation and single molecule experiment. Macromolecules 37, 9242–9256.CrossRefGoogle Scholar
Sim, H.G., Khomami, B. & Sureshkumar, R. 2007 Flow-induced chain scission in dilute polymer solutions: algorithm development and results for scission dynamics in elongational flow. J. Rheol. 51, 1223–1251.CrossRefGoogle Scholar
Soares, E.J. 2020 Review of mechanical degradation and de-aggregation of drag reducing polymers in turbulent flows. J. Non-Newtonian Fluid Mech. 276, 104225.CrossRefGoogle Scholar
Stone, P.A. & Graham, M.D. 2003 Polymer dynamics in a model of the turbulent buffer layer Phys. Fluids 15, 1247–1256.CrossRefGoogle Scholar
Steinberg, V. 2009 Elastic stresses in random flow of a dilute polymer solution and the turbulent drag reduction problem. C. R. Phys. 10, 728–738.CrossRefGoogle Scholar
Thiffeault, J.-L. 2003 Finite extension of polymers in turbulent flow. Phys. Lett. A 308, 445–450.CrossRefGoogle Scholar
Toms, B.A. 1949 Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. In Proceedings of the First International Congress on Rheology, North-Holland, Amsterdam, vol. II, pp. 135–141. North-Holland Publishing Company.Google Scholar
Toms, B.A. 1977 On the early experiments on drag reduction by polymers. Phys. Fluids 20, S3–S5.CrossRefGoogle Scholar
den Toonder, J.M.J., Draad, A.A., Kuiken, G.D.C. & Nieuwstadt, F.T.M. 1995 Degradation effects of dilute polymer solutions on turbulent drag reduction in pipe flows. Appl. Sci. Res. 55, 63–82.CrossRefGoogle Scholar
Vanapalli, S.A., Islam, M.T. & Solomon, M.J. 2005 Scission-induced bounds on maximum polymer drag reduction in turbulent flow. Phys. Fluids 17, 095108.CrossRefGoogle Scholar
Vanapalli, S.A., Ceccio, S.L. & Solomon, M.J. 2006 Universal scaling for polymer chain scission in turbulence. Proc. Natl Acad. Sci. USA 103, 16660–16665.CrossRefGoogle ScholarPubMed
Villermaux, E. 2007 Fragmentation. Annu. Rev. Fluid Mech. 39, 419–446.CrossRefGoogle Scholar
Villermaux, E. 2020 Fragmentation versus cohesion. J. Fluid Mech. 898, P1.CrossRefGoogle Scholar
Vaithianathan, T. & Collins, L.R. 2003 Numerical approach to simulating turbulent flow of a viscoelastic polymer solution. J. Comput. Phys. 187, 1–21.CrossRefGoogle Scholar
Vincenzi, D., Jin, S., Bodenschatz, E. & Collins, L.R. 2007 Stretching of polymers in isotropic turbulence: a statistical closure. Phys. Rev. Lett. 98, 024503.CrossRefGoogle ScholarPubMed
Vincenzi, D., Perlekar, P., Biferale, L. & Toschi, F. 2015 Impact of the Peterlin approximation on polymer dynamics in turbulent flows. Phys. Rev. E 92, 053004.CrossRefGoogle ScholarPubMed
Virk, P.S. 1975 Drag reduction fundamentals. AIChE J. 21, 625–656.CrossRefGoogle Scholar
Watanabe, T. & Gotoh, T. 2010 Coil-stretch transition in an ensemble of polymers in isotropic turbulence. Phys. Rev. E 81, 066301.CrossRefGoogle Scholar
Watanabe, T. & Gotoh, T. 2013 a Hybrid Eulerian–Lagrangian simulations for polymer-turbulence interactions. J. Fluid Mech. 717, 535–575.CrossRefGoogle Scholar
Watanabe, T. & Gotoh, T. 2013 b Kinetic energy spectrum of low-Reynolds-number turbulence with polymer additives. J. Phys.: Conf. Ser. 454, 012007.Google Scholar
Watanabe, T. & Gotoh, T. 2014 Power-law spectra formed by stretching polymers in decaying isotropic turbulence. Phys. Fluids 26, 035110.CrossRefGoogle Scholar
White, C.M. & Mungal, M.G. 2008 Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 40, 235–256.CrossRefGoogle Scholar
Wu, S., Li, C., Zheng, Q. & Xu, L. 2018 Modelling DNA extension and fragmentation in contractive microfluidic devices: a Brownian dynamics and computational fluid dynamics approach. Soft Matt. 14, 8780–8791.CrossRefGoogle ScholarPubMed
Xi, H.-D., Bodenschatz, E. & Xu, H. 2013 Elastic energy flux by flexible polymers in fluid turbulence. Phys. Rev. Lett. 111, 024501.CrossRefGoogle ScholarPubMed
Yeung, P.K. 2002 Lagrangian investigations of turbulence. Annu. Rev. Fluid Mech. 34, 115–142.CrossRefGoogle Scholar