Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T04:22:26.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Plumes in rotating fluid and their transformation into tornados

Published online by Cambridge University Press:  05 August 2021

B.R. Sutherland Open the ORCID record for B.R. Sutherland [Opens in a new window] ,
Y. Ma ,
M.R. Flynn Open the ORCID record for M.R. Flynn [Opens in a new window] ,
D. Frank Open the ORCID record for D. Frank [Opens in a new window] ,
P.F. Linden ,
D. Lemasquerier Open the ORCID record for D. Lemasquerier [Opens in a new window] ,
M. Le Bars Open the ORCID record for M. Le Bars [Opens in a new window] ,
C. Pacary ,
T. Jamin  and
T. Dauxois Open the ORCID record for T. Dauxois [Opens in a new window]
...Show all authors
B.R. Sutherland*
Affiliation:
Department of Physics, University of Alberta, Edmonton, AB T6G 2E1, Canada Department of Earth & Atmospheric Sciences, University of Alberta, Edmonton, AB T6G 2E3, Canada
Y. Ma
Affiliation:
Department of Earth & Atmospheric Sciences, University of Alberta, Edmonton, AB T6G 2E3, Canada
M.R. Flynn
Affiliation:
Department of Mechanical Engineering, University of Alberta, Edmonton, AB T6G 1H9, Canada
D. Frank
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
P.F. Linden
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
D. Lemasquerier
Affiliation:
CNRS, Aix Marseille University, Centrale Marseille, IRPHE, Marseille 13013, France
M. Le Bars
Affiliation:
CNRS, Aix Marseille University, Centrale Marseille, IRPHE, Marseille 13013, France
C. Pacary
Affiliation:
Univ Lyon, ENS de Lyon, CNRS, Laboratoire de Physique, F-69342 Lyon, France
T. Jamin
Affiliation:
Univ Lyon, ENS de Lyon, CNRS, Laboratoire de Physique, F-69342 Lyon, France
T. Dauxois
Affiliation:
Univ Lyon, ENS de Lyon, CNRS, Laboratoire de Physique, F-69342 Lyon, France
S. Joubaud
Affiliation:
Univ Lyon, ENS de Lyon, CNRS, Laboratoire de Physique, F-69342 Lyon, France Institut Universitaire de France (IUF), Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

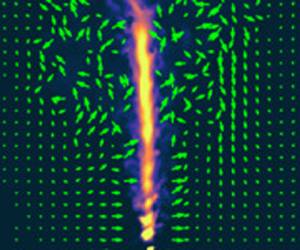
Through laboratory experiments and numerical simulations, we examine the evolution of buoyant plumes as they are influenced by background rotation in a uniform density ambient fluid. The source Rossby number is sufficiently large that rotation does not directly affect the plume at early times. However, on a time scale of the order of half a rotation period, the plume becomes deflected from the vertical axis. For some experiments and simulations, the deflection persists and the flow precesses about the vertical axis. In other cases, shortly after being deflected, the plume laminarizes near the source to form a near-vertical columnar vortex, which we refer to as a ‘tornado’. Tornado formation occurs in some experiments and not in others even if the source and background rotation parameters are identical. However, their formation is more likely if the plumes are ‘lazy’. Simulations reveal that this is a consequence of the competing dynamics that occurs on comparable time scales. As a consequence of entrainment, vertical vorticity builds up within the plume reducing the Rossby number and suppressing vertical motion at distances progressively closer to the source. Meanwhile, the swirl (the ratio of the azimuthal to vertical flow) around the vicinity of the source increases, which tends to suppress three-dimensional turbulence in the near-source flow. Although the former process ultimately acts to deflect the plume off axis, in some instances, the swirl around the source succeeds in laminarizing the flow, resulting in tornado formation.

JFM classification

Convection: Plumes/thermals Geophysical and Geological Flows: Rotating flows Turbulent Flows: Rotating turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 924 , 10 October 2021 , A15
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Batchelor, G.K. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20, 645–658.CrossRefGoogle Scholar
Caulfield, C.P. 1991 Stratification and buoyancy in geophysical flows. PhD thesis, University of Cambridge.Google Scholar
Clarke, R.A. & Gascard, J.-C. 1983 The formation of Labrador Sea Water. Part I: large-scale processes. J. Phys. Oceanogr. 13, 1764–1778.2.0.CO;2>CrossRefGoogle Scholar
Davidson, P.A., Staplehurst, P.J. & Dalziel, S.B. 2006 On the evolution of eddies in a rapidly rotating system. J. Fluid Mech. 557, 135–144.CrossRefGoogle Scholar
Delbende, I., Chomaz, J.-M. & Huerre, P. 1998 Absolute/convective instabilities in the Batchelor vortex: a numerical study of the linear impulse response. J. Fluid Mech. 355, 229–254.CrossRefGoogle Scholar
Delbende, I., Rossi, M. & Le Dizès, S. 2002 Stretching effects on the three-dimensional stability of vortices with axial flow. J. Fluid Mech. 454, 419–442.CrossRefGoogle Scholar
Deremble, B. 2016 Convective plumes in rotating systems. J. Fluid Mech. 799, 27–55.CrossRefGoogle Scholar
Fabregat Tomàs, A., Deremble, B., Wienders, N., Stroman, A., Poje, A.C., Özgökmen, T.M. & Dewar, W.K. 2017 Rotating 2d point source plume models with application to Deepwater Horizon. Ocean Model. 119, 118–135.CrossRefGoogle Scholar
Fabregat Tomàs, A., Dewar, W.K., Özgökmen, T.M., Poje, A.C. & Wienders, N. 2015 Numerical simulations of turbulent thermal, bubble and hybrid plumes. Ocean Model. 90, 16–28.CrossRefGoogle Scholar
Fabregat Tomàs, A., Poje, A.C., Özgökmen, T.M. & Dewar, W.K. 2016 Effects of rotation on turbulent buoyant plumes in stratified environments. J. Geophys. Res. 121 (8), 5397–5417.CrossRefGoogle Scholar
Fernando, H.J.S., Chen, R. & Ayotte, B.A. 1998 Development of a point plume in the presence of background rotation. Phys. Fluids 10 (9), 2369–2383.CrossRefGoogle Scholar
Frank, D., Landel, J.R., Dalziel, S.B. & Linden, P.F. 2017 Anticyclonic precession of a plume in a rotating environment. Geophys. Res. Lett. 44 (18), 9400–9407.CrossRefGoogle Scholar
Frank, D., Landel, J.R., Dalziel, S.B. & Linden, P.F. 2021 Effects of background rotation on the dynamics of multiphase plumes. J. Fluid Mech. 915, A2.CrossRefGoogle Scholar
Greenspan, H.P. & Howard, L.N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17, 385–404.CrossRefGoogle Scholar
Helfrich, K.R. & Battisti, T.M. 1991 Experiments on baroclinic vortex shedding from hydrothermal plumes. J. Geophys. Res. 96 (C7), 12511–12518.CrossRefGoogle Scholar
Hopfinger, E.J., Browand, F.K. & Gagne, Y. 1982 Turbulence and waves in a rotating tank. J. Fluid Mech. 125, 505–534.CrossRefGoogle Scholar
Huang, S. & Li, Q.S. 2009 A new dynamic one-equation subgrid-scale model for large eddy simulations. Intl J. Numer. Meth. Engng 81, 835–865.Google Scholar
Hunt, G.R. & Kaye, N.G. 2001 Virtual origin correction of lazy turbulent plumes. J. Fluid Mech. 435, 377–396.CrossRefGoogle Scholar
Hunt, G.R. & Kaye, N.G. 2005 Lazy plumes. J. Fluid Mech. 533, 329–338.CrossRefGoogle Scholar
Hunt, G.R. & Linden, P.F. 2001 Steady-state flows in an enclosure ventilated by buoyancy forces assisted by wind. J. Fluid Mech. 426, 355–386.CrossRefGoogle Scholar
Jones, H. & Marshall, J. 1993 Convection with rotation in a neutral ocean: a study of open-ocean deep convection. J. Phys. Oceanogr. 23, 1009–1039.2.0.CO;2>CrossRefGoogle Scholar
Kumar, R. & Dewan, A. 2014 Urans computations with buoyancy corrected turbulence models for turbulent thermal plume. Intl J. Heat Mass Transfer 72, 680–689.CrossRefGoogle Scholar
Lessen, M. & Paillet, F. 1974 The stability of a trailing line vortex. Part 2. Viscous theory. J. Fluid Mech. 65, 769–779.CrossRefGoogle Scholar
Lessen, M., Singh, P.J. & Paillet, F. 1974 The stability of a trailing line vortex. Part 1. Inviscid theory. J. Fluid Mech. 63, 753–763.CrossRefGoogle Scholar
Lupton, J.E., Delaney, J.R., Johnson, H.P. & Tivey, M.K. 1985 Entrainment and vertical transport of deep-ocean water by buoyant hydrothermal plumes. Nature 316, 621–623.CrossRefGoogle Scholar
Ma, Y. 2018 Plumes in two-layer stratified fluid with and without background rotation. PhD thesis, University of Alberta.Google Scholar
Martins, F.C., Pereira, J.M.C. & Pereira, J.C.F. 2020 Vorticity transport in laminar steady rotating plumes. Phys. Fluids 32, 043604.CrossRefGoogle Scholar
Maxworthy, T. & Narimousa, S. 1994 Unsteady, turbulent convection into a homogeneous, rotating fluid, with oceanographic applications. J. Phys. Oceanogr. 24, 865–887.2.0.CO;2>CrossRefGoogle Scholar
MEDOC Group 1970 Observation of formation of deep water in the Mediterranean Sea, 1969. Nature 227, 1037–1040.CrossRefGoogle Scholar
Morton, B.R., Taylor, G.I. & Turner, J.S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Pal, A. & Chalamalla, V.K. 2020 Evolution of plumes and turbulent dynamics in deep-ocean convection. J. Fluid Mech. 889, A35.CrossRefGoogle Scholar
van Reeuwijk, M., Salizzoni, P., Hunt, G.R. & Craske, J. 2016 Turbulent transport and entrainment in jets and plumes: a DNS study. Phys. Rev. Fluids 1, 074301.CrossRefGoogle Scholar
Schott, F. & Leaman, K.D. 1991 Observations with moored acoustic Doppler current profiles in the convection regime in the Golfe du Lion. J. Phys. Oceanogr. 21, 558–574.2.0.CO;2>CrossRefGoogle Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. Mon. Weath. Rev. 91, 99–164.2.3.CO;2>CrossRefGoogle Scholar
Sovolofsky, S.A., Adams, E.E. & Sherwood, C.R. 2011 Formation dynamics of subsurface hydrocarbon intrusions following the Deepwater Horizon blowout. Geophys. Res. Lett. 38, L09602.Google Scholar
Speer, K.G. & Marshall, J. 1995 The growth of convective plumes at seafloor hot springs. J. Mar. Res. 53, 1025–1057.CrossRefGoogle Scholar
Staplehurst, P.J., Davidson, P.A. & Dalziel, S.B. 2008 Structure formation in homogeneous freely decaying turbulence. J. Fluid Mech. 598, 81–105.CrossRefGoogle Scholar
Stewartson, K. & Leibovich, S. 1987 On the stability of a columnar vortex to disturbances with large azimuthal wavenumber: the lower neutral points. J. Fluid Mech. 178, 549–566.CrossRefGoogle Scholar
Suzuki, Y.J., Costa, A., Cerminara, M., Esposti Ongaro, T., Herzog, M., Van Eaton, A.R. & Denby, L.C. 2016 Inter-comparison of three-dimensional models of volcanic plumes. J. Volcanol. Geotherm. Res. 326, 26–42.CrossRefGoogle Scholar
Tabor, G. & Baba-Ahmadi, M. 2010 Inlet conditions for large eddy simulation: a review. Comput. Fluids 39, 553–567.CrossRefGoogle Scholar
Vallis, G.K. 2006 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Wang, Y., Chatterjee, P. & de Ris, J.L. 2011 Large eddy simulation of fire plumes. Proc. Combust. Inst. 33, 2473–2480.CrossRefGoogle Scholar
Whitehead, J.A., Marshall, J. & Hufford, G.E. 1996 Localized convection in rotating stratified fluid. J. Geophys. Res. 101 (C11), 25705–25721.CrossRefGoogle Scholar
Yoshizawa, A. 1986 Statistical theory for compressible turbulent shear flows, with application to subgrid modeling. Phys. Fluids 29, 2152–2164.CrossRefGoogle Scholar