Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T10:14:46.101Z Has data issue: false hasContentIssue false
  • English
  • Français

Plume flows in porous media driven by horizontal differential heating

Published online by Cambridge University Press:  06 March 2012

P. Adamou-Graham  and
P. G. Daniels
P. Adamou-Graham
Affiliation:
Centre for Mathematical Science, City University London, Northampton Square, London EC1V 0HB, UK
P. G. Daniels*
Affiliation:
Centre for Mathematical Science, City University London, Northampton Square, London EC1V 0HB, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we describe flow through a porous medium in a two-dimensional rectangular cavity driven by differential heating of the impermeable lower surface. The upper surface is held at constant pressure and at a constant temperature equal to the minimum temperature of the lower surface, while the sidewalls are impermeable and thermally insulated. Numerical results for general values of the Darcy–Rayleigh number 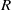and the cavity aspect ratio 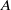are compared with theoretical predictions for the small Darcy–Rayleigh number limit 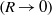where the temperature field is conduction-dominated, and with a boundary-layer theory for the large Darcy–Rayleigh number limit 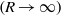where convection is significant. In the latter case a horizontal boundary layer near the lower surface conveys fluid to the hot end of the cavity where it rises to the upper surface in a narrow plume. Predictions are made of the vertical heat transfer through the cavity.

JFM classification

Convection: Convection Convection: Convection in cavities Convection: Convection in porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 696 , 10 April 2012 , pp. 263 - 284
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adamou-Graham, P. 2008 Plume flows in porous media driven by horizontal differential heating, PhD thesis, City University London.Google Scholar
2. Brace, W. F. 1980 Permeability of crystalline and argillaceous rocks. Int. J. Rock Mech. Min. Sci. 17, 241–251.CrossRefGoogle Scholar
3. Cheng, P. 1985 Natural convection in a porous medium: external flows. In Natural Convection: Fundamentals and Applications (ed. Kakac, S., Aung, W. & Viskanta, R. ). Hemisphere.Google Scholar
4. Chery, J., Bonneville, A., Vilotte, J. P. & Yuen, D. 1991 Numerical modelling of caldera dynamic behaviour. Geophys. J. Intl 105, 365–379.CrossRefGoogle Scholar
5. Daniels, P. G. 2007 On the boundary layer structure of differentially heated cavity flow in a stably stratified porous medium. J. Fluid Mech. 586, 347–370.CrossRefGoogle Scholar
6. Daniels, P. G. & Punpocha, M. 2004 Cavity flow in a porous medium driven by differential heating. Intl J. Heat Mass Transfer 47, 3017–3030.CrossRefGoogle Scholar
7. Daniels, P. G. & Punpocha, M. 2005 On the boundary-layer structure of cavity flow in a porous medium driven by differential heating. J. Fluid Mech. 532, 321–344.Google Scholar
8. Daniels, P. G. & Simpkins, P. G. 1984 The flow induced by a heated vertical wall in a porous medium. Q. J. Mech. Appl. Maths 37, 339–354.Google Scholar
9. Horton, C. W. & Rogers, F. T. 1945 Convection currents in a porous medium. J. Appl. Phys. 16, 367–370.Google Scholar
10. Ingham, D. B. & Brown, S. N. 1986 Flow past a suddenly heated vertical plate in a porous medium. Proc. R. Soc. Lond. A403, 51–80.Google Scholar
11. Ingham, D. B., Merkin, J. H. & Pop, I. 1982 Flow past a suddenly cooled vertical flat surface in a saturated porous medium. Intl J. Heat Mass Transfer 25, 1916–1919.CrossRefGoogle Scholar
12. Ingham, D. B. & Pop, I. 1987 Free convection from a semi-infinite vertical surface bounded by a horizontal wall in a porous medium. Intl J. Heat Mass Transfer 30, 1615–1622.Google Scholar
13. Joshi, V. & Gebhart, B. 1984 Vertical natural convection flows in porous media: calculations of improved accuracy. Intl J. Heat Mass Transfer 27, 69–75.CrossRefGoogle Scholar
14. Kohout, F. A. 1965 A hypothesis concerning cyclic flow of salt water related to geothermal heating in the Floridian aquifer. Trans. N. Y. Acad. Sci. 28, 249–271.CrossRefGoogle Scholar
15. Masuoka, T., Tohda, Y., Tsurota, Y. & Yasuda, Y. 1986 Buoyant plume above concentrated heat source in stratified porous media. Trans. JSME Ser. B 52, 2656–2662.Google Scholar
16. Merkin, J. H. 1980 Mixed convection boundary layer flow on a vertical surface in a saturated porous medium. J. Engng Maths 14, 301–313.CrossRefGoogle Scholar
17. Morland, L. W., Zebib, A. & Kassoy, D. R. 1977 Variable property effects on the onset of convection in an elastic porous material. Phys. Fluids 20, 1255–1259.Google Scholar
18. Nield, D. A. 1996 The effect of temperature-dependent viscosity on the onset of convection in a saturated porous medium. Trans. ASME: J. Heat Transfer 118, 803–805.CrossRefGoogle Scholar
19. Nield, D. A. & Bejan, A. 1999 Convection in Porous Media. Springer.CrossRefGoogle Scholar
20. Phillips, O. M. 1991 Flow and Reactions in Permeable Rocks. Cambridge University Press.Google Scholar
21. Rees, D. A. S. 2000 The stability of Darcy–Bénard convection. In Handbook of Porous Media (ed. Vafai, K. ). Marcel Dekker.Google Scholar
22. Rees, D. A. S. 2002 Recent advances in the instability of free convective boundary layers in porous media. In Transport Phenomena in Porous Media II (ed. Ingham, D. B. & Pop, I. ). Elsevier.Google Scholar
23. Rees, D. A. S. & Bassom, A. P. 1991 Some exact solutions for free convection flows over heated semi-infinite surfaces in porous media. Intl J. Heat Mass Transfer 34, 1564–1567.CrossRefGoogle Scholar
24. Rees, D. A. S. & Bassom, A. P. 1993 The nonlinear non-parallel wave instability of boundary-layer flow induced by a horizontal heated surface in porous media. J. Fluid Mech. 253, 267–296.CrossRefGoogle Scholar
25. Rees, D. A. S. & Bassom, A. P. 1994 The linear wave instability of boundary-layer flow induced by a horizontal heated surface in porous media. Intl Commun. Heat Mass Transfer 21, 143–150.CrossRefGoogle Scholar
26. Straus, J. M. & Schubert, G. 1977 Thermal convection of water in a porous medium: effects of temperature- and pressure-dependent thermodynamic and transport processes. J. Geophys. Res. 82, 325–333.CrossRefGoogle Scholar
27. Wooding, R. A. 1963 Convection in a saturated porous medium at large Rayleigh number or Péclet number. J. Fluid Mech. 15, 527–544.CrossRefGoogle Scholar