Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T12:49:04.071Z Has data issue: false hasContentIssue false
  • English
  • Français

Plane shock waves and Haff’s law in a granular gas

Published online by Cambridge University Press:  18 August 2015

M. H. Lakshminarayana Reddy  and
Meheboob Alam
M. H. Lakshminarayana Reddy
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Center for Advanced Scientific Research, Jakkur PO, Bangalore 560064, India
Meheboob Alam*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Center for Advanced Scientific Research, Jakkur PO, Bangalore 560064, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Riemann problem of planar shock waves is analysed for a dilute granular gas by solving Euler- and Navier–Stokes-order equations numerically. The density and temperature profiles are found to be asymmetric, with the maxima of both density and temperature occurring within the shock layer. The density peak increases with increasing Mach number and inelasticity, and is found to propagate at a steady speed at late times. The granular temperature at the upstream end of the shock decays according to Haff’s law (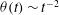${\it\theta}(t)\sim t^{-2}$), but the downstream temperature decays faster than its upstream counterpart. Haff’s law seems to hold inside the shock up to a certain time for weak shocks, but deviations occur for strong shocks. The time at which the maximum temperature deviates from Haff’s law follows a power-law scaling with the upstream Mach number and the restitution coefficient. The origin of the continual build-up of density with time is discussed, and it is shown that the granular energy equation must be ‘regularized’ to arrest the maximum density.

JFM classification

Granular media: Granular media Rarefied Gas Flow: Rarefied Gas Flow Compressible Flows: Shock waves
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 779 , 25 September 2015 , R2
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. & Nott, P. R. 1998 Stability of plane Couette flow of a granular material. J. Fluid Mech. 377, 99–136.Google Scholar
Alam, M., Shukla, P. & Luding, S. 2008 Universality of shear-banding instability and crystallization in sheared granular fluid. J. Fluid Mech. 615, 239–321.Google Scholar
Amarouchene, Y. & Kellay, H. 2006 Speed of sound from shock-fronts in granular flows. Phys. Fluids 18, 031707.Google Scholar
Boudet, J. F., Amarouchene, Y. & Kellay, H. 2008 Shock front width and structure in supersonic granular flows. Phys. Rev. Lett. 101, 254503.Google Scholar
Bougie, J., Moon, S. J., Swift, J. B. & Swinney, H. L. 2002 Shocks in vertically oscillated granular layers. Phys. Rev. E 66, 051301.CrossRefGoogle ScholarPubMed
Buchholtz, V. & Pöschel, T. 1998 Interaction of a granular stream with an obstacle. Granul. Matt. 1, 33–41.CrossRefGoogle Scholar
Carrillo, J. A., Pöschel, T. & Saluena, C. 2008 Granular hydrodynamics and pattern formation in vertically oscillated granular disk layers. J. Fluid Mech. 597, 119–144.Google Scholar
Courant, R. & Friedrichs, K. O. 1948 Supersonic Flows and Shock Waves. Interscience.Google Scholar
Delis, A. I. & Katsaounis, T. 2003 Relaxation schemes for the shallow water equations. Intl J. Numer. Meth. Fluids 41, 695–719.Google Scholar
Esipov, P. & Pöschel, T. 1997 The granular phase diagram. J. Stat. Phys 86, 1385–1395.Google Scholar
Evje, S. & Fjelde, K. K. 2002 Relaxation schemes for the calculation of two-phase flow in pipes. Math. Comput. Model. 36, 535–567.Google Scholar
Forterre, Y. & Pouliquen, O. 2008 Flows of dense granular media. Annu. Rev. Fluid Mech. 40, 1–24.Google Scholar
Garzo, V., Santos, A. & Montanero, J. M. 2007 Modified Sonine approximation for the Navier–Stokes transport coefficients of a granular gas. Physica A 376, 94–107.Google Scholar
Gayen, B. & Alam, M. 2006 Algebraic and exponential instabilities in a sheared micropolar granular fluid. J. Fluid Mech. 567, 195–233.Google Scholar
Gilbarg, D. & Paolucci, D. 1953 The structure of shock waves in the continuum theory of fluids. J. Rat. Mech. Anal. 2, 617–643.Google Scholar
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35, 267–293.Google Scholar
Goldhirsch, I. & Zanetti, G. 1993 Clustering instability in dissipative gases. Phys. Rev. Lett. 70, 1619–1622.Google Scholar
Goldshtein, A. & Shapiro, M. 1995 Mechanics of collisional motion of granular materials. Part 1. General hydrodynamic equations. J. Fluid Mech. 282, 75–114.Google Scholar
Goldshtein, A., Shapiro, M., Moldavsky, L. & Fichman, L. 1995 Mechanics of collisional motion of granular materials. Part 2. Wave propagation through vibrofluidized granular layers. J. Fluid Mech. 287, 349–382.Google Scholar
Gray, J. M. N. T., Tai, Y. C. & Noelle, S. 2003 Shock waves, dead-zones and particle-free regions in rapid granular free surface flows. J. Fluid Mech. 491, 161–181.Google Scholar
Haff, P. K. 1983 Grain flow as a fluid mechanical phenomenon. J. Fluid Mech. 134, 401–430.Google Scholar
Jenkins, J. T. & Savage, S. B. 1983 A theory for the rapid flow of identical, smooth, nearly inelastic, spherical particles. J. Fluid Mech. 130, 187–202.Google Scholar
Jin, S. & Xin, Z. 1995 The relaxation schemes for systems of conservation laws in arbitrary space dimensions. Commun. Pure Appl. Maths. 48, 235–276.Google Scholar
Kamenetsky, V., Goldshtein, A., Shapiro, M. & Degani, D. 2000 Evolution of a shock wave in a granular gas. Phys. Fluids 12, 3036–3049.Google Scholar
Kremer, G. M. & Marques, W. 2011 Fourteen moment theory for granular gases. Kinet. Relat. Models 4, 317–331.Google Scholar
LeVeque, R. J. 2002 Finite Volume Methods for Hyperbolic Conservation Laws. Cambridge University Press.CrossRefGoogle Scholar
Luding, S. & Goldshtein, A. 2002 Collisional cooling with multi-particle interactions. Granul. Matt. 5, 159–163.Google Scholar
Luding, S. & Herrmann, H. J. 1999 Cluster growth in freely cooling granular media. Chaos 8, 673–681.Google Scholar
Nott, P. R. 2011 Boundary conditions at a rigid wall for rough granular gases. J. Fluid Mech. 678, 179–202.Google Scholar
Pöschel, T. & Luding, S. 2001 Granular Gases. Springer.Google Scholar
Prasad, P. 2001 Nonlinear Hyperbolic Waves in Multi-dimensions. Chapman & Hall.Google Scholar
Rericha, E. C., Bizon, C., Shattuck, M. & Swinney, H. L. 2002 Shocks in supersonic sands. Phys. Rev. Lett. 88, 014302.Google Scholar
Saha, S. & Alam, M. 2014 Non-Newtonian stress, collisional dissipation and heat flux in the shear flow of inelastic disks: a reduction via Grad’s moment method. J. Fluid Mech. 757, 251–296.Google Scholar
Sela, N. & Goldhirsch, I. 1998 Hydrodynamic equations for rapid shear flows of smooth, inelastic spheres, to Burnett order. J. Fluid Mech. 361, 41–68.Google Scholar
Torrilhon, M. & Struchtrup, H. 2004 Regularized 13-moment equations: shock structure calculations and comparison to Burnett models. J. Fluid Mech. 513, 171–198.Google Scholar