Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T03:52:16.819Z Has data issue: false hasContentIssue false
  • English
  • Français

Planar hydraulic jumps in thin film flow

Published online by Cambridge University Press:  05 December 2019

Mrinmoy Dhar ,
Gargi Das Open the ORCID record for Gargi Das [Opens in a new window]  and
Prasanta Kumar Das Open the ORCID record for Prasanta Kumar Das [Opens in a new window]
Mrinmoy Dhar
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology, Kharagpur721302, India
Gargi Das
Affiliation:
Department of Chemical Engineering, Indian Institute of Technology, Kharagpur721302, India
Prasanta Kumar Das*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology, Kharagpur721302, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

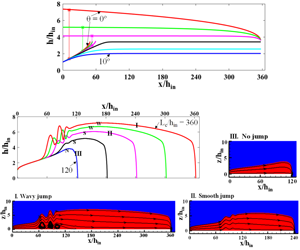
We reformulate shallow water theory to understand viscous shear induced natural hydraulic jumps in channels slightly deviated from the horizontal. One of the interesting contributions of the study is a modified expression for Froude number to predict jumps in inclined channels. The proposed Froude number is different from the conventional expression which incorporates channel inclination as a straight forward component of gravity. This highlights the complexity that a jump can generate even in single phase laminar flow. We also obtain an analytical expression for predicting jump strength and show that the scaling relationship originally proposed for jump location in horizontal channels is applicable for both upslope and downslope flows. As expected, upslope flow aids jump formation and beyond a critical adverse tilt, a submerged jump results in subcritical flow right from the entry. On the other hand, both Reynolds number and channel tilt suppress the tendency to jump in downslope flows and below a critical downslope inclination, the flow remains supercritical throughout the channel length. The film thickness for fully developed flow can be predicted from the exact solution of the Navier–Stokes equations. As the theory encounters a singularity in the jump region, numerical simulations and experimental results have been used to obtain additional insights into the physics of jump formation. They have revealed the existence of submerged jump, wavy jump, smooth jump and no jump conditions as a function of liquid Reynolds number, scaled channel length and channel inclination. Such a variety of jump geometries in planar laminar flow has not been reported earlier. Both theory and simulations also reveal that the linear free surface profile upstream of the jump is a function of Reynolds number only, while the downstream profiles can be tuned by changing both Reynolds number as well as the channel length and tilt over the range of parameters studied. We thus demonstrate that, despite the simplicity and the approximations involved, shallow water equations formulated assuming self-similar velocity profiles can elucidate the physics of planar laminar jumps over slight inclinations, difficult to avoid in practice. The analytical and simulated results have been extensively validated with experimental data obtained from a specially designed test rig which ensures laminar flow before and after the jump. To the authors’ knowledge, almost no experimental study has to date been reported on films ‘thin enough’ to remain laminar even after the planar jump.

JFM classification

Geophysical and Geological Flows: Shallow water flows Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A11
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arakeri, J. H. & Rao, K. P. A. 1996 On radial film flow on a horizontal surface and the circular hydraulic jump. J. Indian Inst. Sci. 76, 73–91.Google Scholar
Beirami, M. K. & Chamani, M. R. 2006 Hydraulic jumps in sloping channels: sequent depth ratio. J. Hydraul. Engng 132, 1061–1068.CrossRefGoogle Scholar
Bhagat, R. K., Jha, N. K., Linden, P. F. & Wilson, D. I. 2018 On the origin of the circular hydraulic jump in a thin liquid film. J. Fluid Mech. 851, R5.CrossRefGoogle Scholar
Bohr, T., Dimon, P. & Putkaradze, V. 1993 Shallow-water approach to the circular hydraulic jump. J. Fluid Mech. 254, 635–648.CrossRefGoogle Scholar
Bohr, T., Putkaradze, V. & Watanabe, S. 1997 Averaging theory for the structure of hydraulic jumps and separation in laminar free-surface flows. Phys. Rev. Lett. 79, 1038–1041.CrossRefGoogle Scholar
Bonn, D., Andersen, A. & Bohr, T. 2009 Hydraulic jumps in a channel. J. Fluid Mech. 618, 71–87.CrossRefGoogle Scholar
Bowles, R. I. & Smith, F. T. 1992 The standing hydraulic jump: theory, computations and comparisons with experiments. J. Fluid Mech. 242, 145–168.CrossRefGoogle Scholar
Bush, J. W. M. & Aristoff, J. M. 2003 The influence of surface tension on the circular hydraulic jump. J. Fluid Mech. 489, 229–238.CrossRefGoogle Scholar
Chanson, H. & Chachereau, Y. 2013 Scale effects affecting two-phase flow properties in hydraulic jump with small inflow Froude number. Exp. Therm. Fluid Sci. 45, 234–242.CrossRefGoogle Scholar
Chanson, H. & Montes, J. S. 1995 Characteristics of undular hydraulic jumps: experimental apparatus and flow patterns. J. Hydraul. Engng ASCE 121, 129–144.CrossRefGoogle Scholar
Chippada, S., Ramaswamy, B. & Wheeler, M. F. 1994 Numerical simulation of hydraulic jump. Intl J. Numer. Meth. Engng 37, 1381–1397.CrossRefGoogle Scholar
Chow, V. T. 1959 Open-Channel Hydraulics. McGraw-Hill.Google Scholar
Craik, A. D. D., Latham, R. C., Fawises, M. J. & Gribbon, P. W. F. 1981 The circular hydraulic jump. J. Fluid Mech. 112, 347–362.CrossRefGoogle Scholar
Dasgupta, R. & Tomar, G. 2015 Viscous undular hydraulic jumps of moderate Reynolds number flows. Proc. IUTAM 15, 300–304.CrossRefGoogle Scholar
Dasgupta, R., Tomar, G. & Govindarajan, R. 2015 Numerical study of laminar, standing hydraulic jumps in a planar geometry. Eur. Phys. J. E 38, 1–14.Google Scholar
Duchesne, A., Lebon, L. & Limat, L. 2014 Constant Froude number in a circular hydraulic jump and its implication on the jump radius selecion. Eur. Phys. Lett. 107 (5), 54002.Google Scholar
Higuera, F. J. 1994 The hydraulic jump in a viscous laminar flow. J. Fluid Mech. 274, 69–92.CrossRefGoogle Scholar
Higuera, F. J. 1997 The circular hydraulic jump. Phys. Fluids 9, 1476–1478.CrossRefGoogle Scholar
Kasimov, A. R. 2008 A stationary circular hydraulic jump, the limits of its existence and its gasdynamic analogue. J. Fluid Mech. 601, 189–198.CrossRefGoogle Scholar
Kate, R. P., Das, P. K. & Chakraborty, S. 2007a An experimental investigation on the interaction of hydraulic jumps formed by two normal impinging circular liquid jets. J. Fluid Mech. 590, 355–380.CrossRefGoogle Scholar
Kate, R. P., Das, P. K. & Chakraborty, S. 2007b Hydraulic jumps due to oblique impingement of circular liquid jets on a flat horizontal surface. J. Fluid Mech. 573, 247–263.CrossRefGoogle Scholar
Kate, R. P., Das, P. K. & Chakraborty, S. 2008 An investigation on non-circular hydraulic jumps formed due to obliquely impinging circular liquid jets. Exp. Therm. Fluid Sci. 32, 1429–1439.CrossRefGoogle Scholar
Liu, X. & Lienhard, J. H. V. 1993 The hydraulic jump in circular jet impingement and in other thin liquid films. Exp. Fluids 15, 108–116.CrossRefGoogle Scholar
Meftah, M. B., Mossa, M. & Pollio, A. 2010 Considerations on shock wave/boundary layer interaction in undular hydraulic jumps in horizontal channels with a very high aspect ratio. Eur. J. Mech. (B/Fluids) 29, 415–429.CrossRefGoogle Scholar
Mohajer, B. & Li, R. 2015 Circular hydraulic jump on finite surfaces with capillary limit. Phys. Fluids 27, 117102.CrossRefGoogle Scholar
Montes, J. S. & Chanson, H. 1998 Characteristics of undular hydraulic jumps: experiments and analysis. J. Hydraul. Engng ASCE 124, 192–205.CrossRefGoogle Scholar
Mortazavi, M., Chenadec, V. L., Moin, P. & Mani, A. 2016 Direct numerical simulation of a turbulent hydraulic jump: turbulence statistics and air entrainment. J. Fluid Mech. 797, 60–94.CrossRefGoogle Scholar
Passandideh-Fard, M., Teymourtash, A. R. & Khavari, M. 2011 Numerical study of circular hydraulic jump using volume-of-fluid method. Trans. ASME J. Fluids Engng 133, 011401.CrossRefGoogle Scholar
Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 190, 572–600.CrossRefGoogle Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228, 5838–5866.CrossRefGoogle Scholar
Rayleigh, L. 1914 On the theory of long waves and bores. Proc. R. Soc. Lond. A 90, 324–328.CrossRefGoogle Scholar
Richard, G. L. & Gavrilyuk, S. L. 2013 The classical hydraulic jump in a model of shear shallow-water flows. J. Fluid Mech. 725, 492–521.CrossRefGoogle Scholar
Ruschak, K. J., Weinstein, S. J. & Ng, K. 2001 Developing film flow on an inclined plane with a critical point. Trans. ASME J. Fluids Engng 123, 698–709.CrossRefGoogle Scholar
Singh, D. & Das, A. K. 2018 Computational simulation of radially asymmetric hydraulic jumps and jump–jump interactions. Comput. Fluids 170, 1–12.CrossRefGoogle Scholar
Singha, S. B., Bhattacharjee, J. K. & Ray, A. K. 2005 Hydraulic jump in one-dimensional flow. Eur. Phys. J. B 426, 417–426.CrossRefGoogle Scholar
Tani, I. 1949 Water jump in the boundary layer. J. Phys. Soc. Japan 4, 212–215.CrossRefGoogle Scholar
Vishwanath, K. P., Dasgupta, R., Govindarajan, R. & Sreenivas, K. R. 2016 The effect of initial momentum flux on the circular hydraulic jump. Trans. ASME J. Fluids Engng 137, 1–7.Google Scholar
Watanabe, S., Putkaradze, V. & Bohr, T. 2003 Integral methods for shallow free-surface flows with separation. J. Fluid Mech. 480, 233–265.CrossRefGoogle Scholar
Watson, E. J. 1964 The radial spread of a liquid jet over a horizontal plane. J. Fluid Mech. 20, 481–499.CrossRefGoogle Scholar
Witt, A., Gulliver, J. & Shen, L. 2015 Simulating air entrainment and vortex dynamics in a hydraulic jump. Intl J. Multiphase Flow 72, 165–180.CrossRefGoogle Scholar
Witt, A., Gulliver, J. S. & Shen, L. 2018 Numerical investigation of vorticity and bubble clustering in an air entraining hydraulic jump. Comput. Fluids 172, 162–180.CrossRefGoogle Scholar
Yokoi, K. & Xiao, F. 2002 Mechanism of structure formation in circular hydraulic jumps: numerical studies of strongly deformed free-surface shallow flows. Physica D 161, 202–219.Google Scholar