Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-01T03:39:42.018Z Has data issue: false hasContentIssue false
  • English
  • Français

Phase-averaged equation for water waves

Published online by Cambridge University Press:  08 February 2013

Odin Gramstad  and
Michael Stiassnie
Odin Gramstad*
Affiliation:
Department of Mathematics, University of Oslo, PO Box 1053 Blindern, NO-0316 Oslo, Norway
Michael Stiassnie
Affiliation:
Faculty of Civil and Environmental Engineering, Technion IIT, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

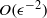We investigate phase-averaged equations describing the spectral evolution of dispersive water waves subject to weakly nonlinear quartet interactions. In contrast to Hasselmann’s kinetic equation, we include the effects of near-resonant quartet interaction, leading to spectral evolution on the ‘fast’ $O({\epsilon }^{- 2} )$ time scale, where $\epsilon $ is the wave steepness. Such a phase-averaged equation was proposed by Annenkov & Shrira (J. Fluid Mech., vol. 561, 2006b, pp. 181–207). In this paper we rederive their equation taking some additional higher-order effects related to the Stokes correction of the frequencies into account. We also derive invariants of motion for the phase-averaged equation. A numerical solver for the phase-averaged equation is developed and successfully tested with respect to convergence and conservation of invariants. Numerical simulations of one- and two-dimensional spectral evolution are performed. It is shown that the phase-averaged equation describes the ‘fast’ evolution of a spectrum on the 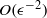$O({\epsilon }^{- 2} )$ time scale well, in good agreement with Monte-Carlo simulations using the Zakharov equation and in qualitative agreement with known features of one- and two-dimensional spectral evolution. We suggest that the phase-averaged equation may be a suitable replacement for the kinetic equation during the initial part of the evolution of a wave field, and in situations where ‘fast’ field evolution takes place.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 718 , 10 March 2013 , pp. 280 - 303
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Annenkov, S. Y. & Shrira, V. I. 2006a Direct numerical simulation of downshift and inverse cascade for water wave turbulence. Phys. Rev. Lett. 96 (20), 204501.Google Scholar
Annenkov, S. Y. & Shrira, V. I. 2006b Role of non-resonant interactions in the evolution of nonlinear random water wave fields. J. Fluid Mech. 561, 181–207.Google Scholar
Annenkov, S. Y. & Shrira, V. I. 2009 Fast nonlinear evolution in wave turbulence. Phys. Rev. Lett. 102 (2), 024502.CrossRefGoogle ScholarPubMed
Babanin, A. V., Chalikov, D., Young, I. R. & Savelyev, I. 2007 Predicting the breaking onset of surface water waves. Geophys. Res. Lett. 34 (7)L07605.CrossRefGoogle Scholar
Babanin, A. V., Chalikov, D., Young, I. R. & Savelyev, I. 2010 Numerical and laboratory investigation of breaking of steep two-dimensional waves in deep water. J. Fluid Mech. 644, 433–463.CrossRefGoogle Scholar
Cooker, M. J., Peregrine, D. H., Vidal, C. & Dold, J. W. 1990 The interaction between a solitary wave and a submerged semicircular cylinder. J. Fluid Mech. 215, 1–22.CrossRefGoogle Scholar
Dold, J. W. & Peregrine, D. H. 1986 An efficient boundary integral method for steep unsteady water waves. In Numerical Methods for Fluid Dynamics II (ed. Morton, K. W. & Baines, M. J.). pp. 671–679. Oxford University Press.Google Scholar
Dyachenko, A. I. & Zakharov, V. E. 1994 Is free-surface hydrodynamics an integrable system? Phys. Lett. A 190 (2), 144–148.Google Scholar
Dysthe, K. B., Trulsen, K., Krogstad, H. E. & Socquet-Juglard, H. 2003 Evolution of a narrow-band spectrum of random surface gravity waves. J. Fluid Mech. 478, 1–10.Google Scholar
Gramstad, O, Agnon, Y & Stiassnie, M 2011 The localized Zakharov equation: derivation and validation. Eur. J. Mech. B 30 (2), 137–146.Google Scholar
Hasselmann, K. 1962 On the nonlinear energy transfer in a gravity-wave spectrum. Part 1. General theory. J. Fluid Mech. 12, 481–500.Google Scholar
Janssen, P. A. E. M. 2003 Nonlinear four-wave interactions and freak waves. J. Phys. Oceanogr. 33 (4), 863–884.2.0.CO;2>CrossRefGoogle Scholar
Janssen, P. A. E. M. 2004 The Interaction of Ocean Waves and Wind. Cambridge University Press.CrossRefGoogle Scholar
Krasitskii, V. P. 1994 On reduced equations in the Hamiltonian theory of weakly nonlinear surface-waves. J. Fluid Mech. 272, 1–20.Google Scholar
Lvov, Y. V., Binder, R. & Newell, A. C. 1998 Quantum weak turbulence with applications to semiconductor lasers. Phys. Nonlinear Phenom. 121 (3–4), 317–343.CrossRefGoogle Scholar
Mei, C. C., Stiassnie, M. & Yue, D. K. P. 2005 Theory and Applications of Ocean Surface Waves, Part 2: Nonlinear Aspects. Advanced Series on Ocean Engineering , vol. 23. World Scientific.Google Scholar
Phillips, O. M. 1960 On the dynamics of unsteady gravity waves of finite amplitude. 1. The elementary interactions. J. Fluid Mech. 9, 193–217.CrossRefGoogle Scholar
Stiassnie, M. & Shemer, L. 1984 On modifications of the Zakharov equation for surface gravity-waves. J. Fluid Mech. 143, 47–67.Google Scholar
Stiassnie, M. & Shemer, L. 2005 On the interaction of four water-waves. Wave Motion 41 (4), 307–328.Google Scholar
van Vledder, G. P. & Holthuijsen, L. H. 1993 The directional response of ocean waves to turning winds. J. Phys. Oceanogr. 23 (2), 177–192.Google Scholar
Waseda, T., Toba, Y. & Tulin, M. P. 2001 Adjustment of wind waves to sudden changes of wind speed. J. Oceanogr. 57 (5), 519–533.Google Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9, 190–194.Google Scholar
Zakharov, V. E., L’vov, V. S. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence. Springer.Google Scholar