Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T21:27:34.679Z Has data issue: false hasContentIssue false
  • English
  • Français

Phase dynamics of freely swimming foils

Published online by Cambridge University Press:  02 July 2014

Cyndee L. Finkel  and
Karl D. von Ellenrieder
Cyndee L. Finkel
Affiliation:
Department of Physics, Florida Atlantic University, Boca Raton, FL 33431, USA
Karl D. von Ellenrieder*
Affiliation:
Department of Ocean and Mechanical Engineering, Florida Atlantic University, Dania Beach, FL 33004, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A two-dimensional D-shaped cylinder and heaving foil were mounted in tandem and used to simulate the main body and tail, respectively, of a natural swimmer. Thrust/drag measurements of the force on the foil and particle image velocimetry measurements of the flow downstream of the swimming system were conducted at a Reynolds number of about 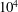$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}10^4$ in a water channel with a constant free stream current speed. Two main sets of measurements were conducted: one set with the swimming system locked at a fixed streamwise location in the water channel as the heave frequency of the foil was varied; the other set with the system freely swimming to a desired set-point position from different upstream and downstream locations. When the freely swimming system reached and maintained its set-point position, so that its swimming speed matched that of the current, the oscillation frequency of the heaving foil corresponded to a Strouhal number of 0.36. Phase portraits of the measured thrust/drag forces reveal limit cycle oscillations for all swimming cases studied, which suggests that self-regulation drives the selection of this Strouhal number. No coupling was observed between the vortices shed by the D-shaped cylinder and the self-selected frequency of the heaving foil during free swimming. An examination of the ratio of the phase-locking indices for the input heaving motion of the foil and the coupled fluidic thrust/drag response reveals that it approaches a value of 0.5 over time when the freely swimming system is released from rest and allowed to achieve steady-state cruising. The jet produced by the freely swimming foil was inclined at an angle of approximately 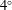$4^\circ $ with respect to the direction of the mean flow.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Swimming/flying
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 5 - 21
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. M., Streitlien, K., Barrett, D. S. & Triantafyllou, M. S. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.Google Scholar
Bandyopadhyay, P. R. & Leinhos, H. A. 2013 Propulsion efficiency of bodies appended with multiple flapping fins: when more is less. Phys. Fluids 25, 041902.Google Scholar
Beal, D. N., Hover, F. S., Triantafyllou, M. S., Liao, J. C. & Lauder, G. V. 2006 Passive propulsion in vortex wakes. J. Fluid Mech. 549, 385–402.Google Scholar
Bishop, R. E. D. & Hassan, A. Y. 1964 The lift and drag forces on a circular cylinder in a flowing fluid. Proc. R. Soc. Lond. A 7 277 (1368), 32–50.Google Scholar
Boashash, B. 1992 Estimating and interpreting the instantaneous frequency of a signal – part 1: fundamentals. Proc. IEEE 80 (4), 520–538.Google Scholar
von Ellenrieder, K. D., Parker, K. & Soria, J. 2008 Fluid mechanics of flapping wings. Exp. Therm. Fluid Sci. 32 (8), 1578–1589.Google Scholar
von Ellenrieder, K. D. & Pothos, S. 2008 PIV measurements of the asymmetric wake of a two dimensional heaving hydrofoil. Exp. Fluids 44, 733–745.Google Scholar
Eloy, C. 2012 Optimal Strouhal number for swimming animals. J. Fluids Struct. 30, 205–218.Google Scholar
Finkel, C. L. 2013 Synchronization and phase dynamics of oscillating foils. PhD thesis, Florida Atlantic University, Boca Raton, FL, USA.Google Scholar
Franklin, G. F., Powell, J. D. & Emami-Naeini, A. 1994 Feedback Control of Dynamic Systems, 3rd edn. Addison-Wesley.Google Scholar
Godoy-Diana, R., Aider, J.-L. & Wesfreid, J. E. 2008 Transitions in the wake of a flapping foil. Phys. Rev. E 77 (1), 016308.CrossRefGoogle ScholarPubMed
Godoy-Diana, R., Marais, C., Aider, J. L. & Wesfreid, J. E. 2009 A model for the symmetry breaking of the reverse Bérnard–von Kármán vortex street produced by a flapping foil. J. Fluid Mech. 622, 23–32.CrossRefGoogle Scholar
Gopalkrishnan, R., Triantafyllou, M. S., Triantafyllou, G. S. & Barrett, D. 1994 Active vorticity control in a shear flow using a flapping foil. J. Fluid Mech. 274, 1–21.Google Scholar
Heathcote, S. & Gursul, I. 2007 Jet switching phenomenon for a periodically plunging airfoil. Phys. Fluids 19 (2), 027104.Google Scholar
Jones, K. D., Dohring, C. M. & Platzer, M. P. 1988 Experimental and computational investigation of the Knoller–Betz effect. AIAA J. 36 (7), 1240–1246.CrossRefGoogle Scholar
Kundu, P. K. & Cohen, I. M. 2004 Fluid Mechanics, 3rd edn. Elsevier Inc.Google Scholar
Liao, Q., Dong, G. J. &  Lu, X. Y. 2004 Vortex formation and force characteristics of a foil in the wake of a circular cylinder. J. Fluid Struct. 19, 491–510.Google Scholar
Lighthill, M. J. 1971 Large-amplitude elongated-body theory of fish locomotion. Proc. R. Soc. Lond. B 179 (1055), 125–138.Google Scholar
Pikovsky, A., Rosenblum, M. & Kurths, J. 2003 Synchronization: a Universal Concept in Nonlinear Sciences. vol. 12. Cambridge University Press.Google Scholar
Pikovsky, A. S., Rosenblum, M. G., Osipov, G. V. & Kurths, J. 1997 Phase synchronization of chaotic oscillators by external driving. Physica D 104, 219–238.Google Scholar
Przybilla, A., Kunze, S., Rudert, A., Bleckmann, H. & Brücker, C. 2010 Entraining in trout: a behavioural and hydrodynamic analysis. J. Expl Biol. 213, 2976–2986.Google Scholar
Read, D. A., Hover, F. S. & Triantafyllou, M. S. 2003 Forces on oscillating foils for propulsion and maneuvering. J. Fluid Struct. 17, 163–183.Google Scholar
Ren, Wei, Hu, Hui, Liu, Hong &  Wu, James C 2013 An experimental investigation on the asymmetric wake formation of an oscillating airfoil. AIAA paper 2013-0794.Google Scholar
Rohr, J. J. & Fish, F. E. 2004 Strouhal numbers and optimization of swimming by odontocete cetaceans. J. Expl Biol. 207, 1633–1642.Google Scholar
Rosenblum, M., Pikovsky, A., Kurths, J., Schäfer, C. & Tass, P. A. 2001 Phase synchronization: from theory to data analysis. Handbook of Biological Physics, vol. 4. Elsevier Science.Google Scholar
Rosenblum, M. G., Pikovsky, A. S. & Kurths, J. 1996 Phase synchronization of chaotic oscillators. Phys. Rev. Lett. 76 (11), 1804–1807.Google Scholar
Streitlien, K., Triantafyllou, G. S. & Triantafyllou, M. S 1996 Efficient foil propulsion through vortex control. AIAA J. 34 (11), 2315–2319.Google Scholar
Strogatz, S. H. 1994 Nonlinear Dynamics and Chaos. Perseus Books.Google Scholar
Taylor, G. K., Nudds, R. L. & Thomas, A. L. R. 2003 Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 425, 707–711.Google Scholar
Triantafyllou, G. S., Triantafyllou, M. S. & Grosenbaugh, M. A. 1993 Optimal thrust development in oscillating foils with application to fish propulsion. J. Fluids Struct. 7 (2), 205–224.CrossRefGoogle Scholar
Triantafyllou, M. S., Triantafyllou, G. S. & Gopalkrishnan, R. 1991 Wake mechanics for thrust generation in oscillating foils. Phys. Fluids A 3 (12), 2835–2837.Google Scholar
Triantafyllou, M. S., Triantafyllou, G. S. & Yue, D. K. P. 2000 Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 32 (1), 33–53.Google Scholar
Vandenberghe, N., Zhang, J. & Childress, S. 2004 Symmetry breaking leads to forward flapping flight. J. Fluid Mech. 506, 147–155.Google Scholar
Wu, T. Y.-T. 1961 Swimming of a waving plate. J. Fluid Mech. 10 (03), 321–344.Google Scholar