Article contents
Perturbative corrections for the scaling of heat transport in a Hele-Shaw geometry and its application to geological vertical fractures
Published online by Cambridge University Press: 11 February 2019
Abstract
In this work, we investigate numerically the perturbative effects of cell aperture in heat transport and thermal dissipation rate for a vertical Hele-Shaw geometry, which is used as an analogue representation of a planar vertical fracture at the laboratory scale. To model the problem, we derive a two-dimensional set of equations valid for this geometry. For Hele-Shaw cells heated from below and above, with periodic boundary conditions in the horizontal direction, the model gives new nonlinear scalings for both the time-averaged Nusselt number 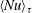 $\langle Nu\rangle _{\unicode[STIX]{x1D70F}}$ and dimensionless mean thermal dissipation rate
$\langle Nu\rangle _{\unicode[STIX]{x1D70F}}$ and dimensionless mean thermal dissipation rate 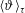 $\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}$ in the high-Rayleigh regime. We demonstrate that
$\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}$ in the high-Rayleigh regime. We demonstrate that 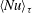 $\langle Nu\rangle _{\unicode[STIX]{x1D70F}}$ and
$\langle Nu\rangle _{\unicode[STIX]{x1D70F}}$ and 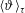 $\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}$ depend upon the cell anisotropy ratio
$\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}$ depend upon the cell anisotropy ratio  $\unicode[STIX]{x1D716}$, which measures the ratio between the cell gap and height. We show that
$\unicode[STIX]{x1D716}$, which measures the ratio between the cell gap and height. We show that 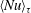 $\langle Nu\rangle _{\unicode[STIX]{x1D70F}}$ values in the high-Rayleigh regime decrease when
$\langle Nu\rangle _{\unicode[STIX]{x1D70F}}$ values in the high-Rayleigh regime decrease when  $\unicode[STIX]{x1D716}$ grows, supporting the field observations at the fracture scale. When
$\unicode[STIX]{x1D716}$ grows, supporting the field observations at the fracture scale. When 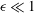 $\unicode[STIX]{x1D716}\ll 1$, our results are in agreement with the scalings found using the Darcy model. The numerical results satisfy the theoretical relation
$\unicode[STIX]{x1D716}\ll 1$, our results are in agreement with the scalings found using the Darcy model. The numerical results satisfy the theoretical relation 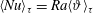 $\langle Nu\rangle _{\unicode[STIX]{x1D70F}}=Ra\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}$, which is obtained from the model. This latter relation is valid for all values of Rayleigh number considered. The perturbative effects of cell aperture are observed only in the exponents of the scalings
$\langle Nu\rangle _{\unicode[STIX]{x1D70F}}=Ra\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}$, which is obtained from the model. This latter relation is valid for all values of Rayleigh number considered. The perturbative effects of cell aperture are observed only in the exponents of the scalings 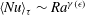 $\langle Nu\rangle _{\unicode[STIX]{x1D70F}}\sim Ra^{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D716})}$ and
$\langle Nu\rangle _{\unicode[STIX]{x1D70F}}\sim Ra^{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D716})}$ and 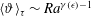 $\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}\sim Ra^{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D716})-1}$.
$\langle \unicode[STIX]{x1D717}\rangle _{\unicode[STIX]{x1D70F}}\sim Ra^{\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D716})-1}$.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 28
- Cited by



