Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-12-01T06:22:46.501Z Has data issue: false hasContentIssue false
  • English
  • Français

The persistence of large-scale circulation in Rayleigh–Bénard convection

Published online by Cambridge University Press:  12 August 2021

Ping Wei Open the ORCID record for Ping Wei [Opens in a new window]
Ping Wei*
Affiliation:
School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

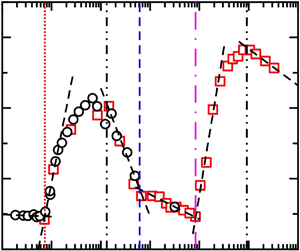
The time-averaged strength $\langle \delta \rangle /\varDelta$ of a convective cellular pattern and large-scale circulation (LSC) in the turbulence regime of turbulent Rayleigh–Bénard convection exhibits a sequence of sharp changes with the Rayleigh number $Ra$. Changes occur when $Ra$ reaches transition values between the conduction, convection, chaotic, transition, soft turbulence and hard turbulence regimes. Measurements were taken from two cylindrical cells with Plexiglas walls and nitrogen gas as the working fluid. The data cover the range $10^{3} \lesssim Ra \lesssim 10^{9}$ at $Pr = 0.72$, where $Pr$ is the Prandtl number and $\varGamma \equiv D/H=1.00$ is the aspect ratio (diameter over height). The cellular pattern strength $\delta$ grows continuously as $Ra$ exceeds the critical value $Ra_c=7300$ for the wall admittance $C=2.02$ in the convection regime. In the oscillation regime, the temperature power spectra at the sidewall show an oscillatory frequency peak. In the chaotic regime, δ is diminished as $Ra$ increases. In the transition regime, $\langle \delta \rangle /\varDelta$ continues to decrease, nearly to 0. Under soft turbulence where the LSC is formed, $\langle \delta \rangle$ grows with $Ra$ as a cellular pattern in the convection regime, suggesting that LSC reflects a cellular pattern. Under hard turbulence, the LSC flow strength decreases as $Ra$ increases. The Reynolds number $Re$ was also measured based on the LSC turnover time, and it was found that two power laws, $\langle \delta \rangle /\varDelta \times Ra/Pr = 0.007Re^{3.0}$ and $\langle \delta \rangle /\varDelta \times Ra/Pr = 15.4Re^{1.76}$, fit the data for $Re<400$ and $Re>400$, respectively.

JFM classification

Convection: Buoyancy-driven instability Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 924 , 10 October 2021 , A28
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlers, G. 2009 Turbulent convection. Physics 2, 74.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–538.CrossRefGoogle Scholar
Bai, K., Ji, D. & Brown, E. 2016 Ability of a low-dimensional model to predict geometry-dependent dynamics of large-scale coherent structures in turbulence. Phys. Rev. E 93, 023117.CrossRefGoogle ScholarPubMed
Brent, A.D., Voller, V.R. & Reid, K.J. 1988 Enthalpy-porosity technique for modeling convection-diffusion phase change – application to the melting of a pure metal. Numer. Heat Transfer 13, 297–318.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2006 Effect of the Earth's Coriolis force on turbulent Rayleigh–Bénard convection in the laboratory. Phys. Fluids 18, 125108.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2007 Temperature gradients and search for non-Boussinesq effects in the interior of turbulent Rayleigh–Bénard convection. Europhys. Lett. 80, 14001.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2008 a Azimuthal asymmetries of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20, 105105.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2008 b A model of diffusion in a potential well for the dynamics of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20, 075101.CrossRefGoogle Scholar
Brown, E., Funfschilling, D. & Ahlers, G. 2007 Anomalous Reynolds-number scaling in turbulent Rayleigh–Bénard convection. J. Stat. Mech. 2007, P10005.CrossRefGoogle Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 a Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.CrossRefGoogle ScholarPubMed
Brown, E., Nikolaenko, A., Funfschilling, D. & Ahlers, G. 2005 b Heat transport by turbulent Rayleigh–Bénard convection: effect of finite top- and bottom-plate conductivity. Phys. Fluids 17, 075108.CrossRefGoogle Scholar
Buell, J.C. & Catton, I. 1983 Effects of rotation on the stability of a bounded cylindrical layer of fluid heated from below. Phys. Fluids 26, 892.CrossRefGoogle Scholar
Busse, F.H. 2003 The sequence-of-bifurcations approach towards understanding turbulent fluid flow. Surv. Geophys. 24, 269–288.CrossRefGoogle Scholar
Chandra, M. & Verma, M.K. 2011 Dynamics and symmetries of flow reversals in turbulent convection. Phys. Rev. E 83, 067303.CrossRefGoogle ScholarPubMed
Chandra, M. & Verma, M.K. 2013 Flow reversals in turbulent convection via vortex reconnections. Phys. Rev. Lett. 110, 114503.CrossRefGoogle ScholarPubMed
Charlson, G.S. & Sani, R.L. 1970 Thermoconvective instability in a bounded cylindrical fluid layer. Intl J. Heat Mass Transfer 13, 1479–1496.CrossRefGoogle Scholar
Charlson, G.S. & Sani, R.L. 1971 On thermoconvective instability in a bounded cylindrical fluid layer. Intl J. Heat Mass Transfer 14, 2157–2160.CrossRefGoogle Scholar
Foroozani, N., Niemela, J.J., Armenio, V. & Sreenivasan, K.R. 2017 Reorientations of the large-scale flow in turbulent convection in a cube. Phys. Rev. E 95, 033107.CrossRefGoogle Scholar
Funfschilling, D., Brown, E. & Ahlers, G. 2008 Torsional oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 607, 119–139.CrossRefGoogle Scholar
Hartlep, T., Tilgner, A. & Busse, F.H. 2005 Transition to turbulent convection in a fluid layer heated from below at moderate aspect ratio. J. Fluid Mech. 544, 309–322.CrossRefGoogle Scholar
Hartmann, D.L., Moy, L.A. & Fu, Q. 2001 Tropical convection and the energy balance at the top of the atmosphere. J. Clim. 14, 4495–4511.2.0.CO;2>CrossRefGoogle Scholar
He, X., Bodenschatz, E. & Ahlers, G. 2016 Azimuthal diffusion of the large-scale-circulation plane, and absence of significant non-Boussinesq effects, in turbulent convection near the ultimate-state transition. J. Fluid Mech. 791, R3.CrossRefGoogle Scholar
Hébert, F., Hufschmid, R., Scheel, J. & Ahlers, G. 2010 Onset of Rayleigh–Bénard convection in cylindrical containers. Phys. Rev. E 81 (4), 046318.CrossRefGoogle ScholarPubMed
Heslot, F., Castaing, B. & Libchaber, A. 1987 Transition to turbulence in helium gas. Phys. Rev. A 36, 5870–5873.CrossRefGoogle Scholar
Hunt, G.R. & Linden, P.F. 1999 The fluid mechanics of natural ventilation – displacement ventilation by buoyancy-driven flows assisted by wind. Build. Environ. 34, 707–720.CrossRefGoogle Scholar
Jeffreys, H. 1928 Some cases of instability in fluid motion. Proc. R. Soc. Lond. A 118 (779), 195–208.Google Scholar
Ji, D. & Brown, E. 2020 Low-dimensional model of the large-scale circulation of turbulent Rayleigh–Bénard convection in a cubic container. Phys. Rev. Fluids 5, 064606.CrossRefGoogle Scholar
Krishnamurti, R. & Howard, L.N. 1981 Large scale flow generation in turbulent convection. Proc. Natl Acad. Sci. USA 78, 1981–1985.CrossRefGoogle ScholarPubMed
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Mamykin, A.D., Kolesnichenko, I.V., Pavlinov, A.M. & Khalilov, R.I. 2018 Large scale circulation in turbulent Rayleigh–Bénard convection of liquid sodium in cylindrical cell. J. Phys.: Conf. Ser. 1128, 012019.Google Scholar
Marshall, J. & Schott, F. 1999 Open-ocean convection: observations, theory, and models. Rev. Geophys. 37, 1–64.CrossRefGoogle Scholar
Mishra, P.K., De, A.K., Verma, M.K. & Eswaran, V. 2011 Dynamics of reorientations and reversals of large-scale flow in Rayleigh–Bénard convection. J. Fluid Mech. 668, 480–499.CrossRefGoogle Scholar
Mueller, K.H., Ahlers, G. & Pobell, F. 1976 Thermal expansion coefficient, scaling, and universality near the superfluid transition of $^{4}\mathrm {He}$under pressure. Phys. Rev. B 14, 2096–2118.CrossRefGoogle Scholar
Müller, G., Neumann, G. & Weber, W. 1984 Natural convection in vertical bridgeman configurations. J. Cryst. Growth 70, 78–93.CrossRefGoogle Scholar
Musilová, V., Kréalíík, T., La Mantia, M., Macek, M., Urban, P. & Skrbek, L. 2017 Reynolds number scaling in cryogenic turbulent Rayleigh–Bénard convection in a cylindrical aspect ratio one cell. J. Fluid Mech. 832, 721–744.CrossRefGoogle Scholar
Ni, R., Huang, S.-D. & Xia, K.-Q. 2015 Reversals of the large-scale circulation in quasi-2D Rayleigh–Bénard convection. J. Fluid Mech. 778, R5.CrossRefGoogle Scholar
Rahmstorf, S. 2000 The thermohaline ocean circulation: a system with dangerous thresholds? Clim. Change 46, 247–256.CrossRefGoogle Scholar
Sakievich, P.J., Peet, Y.T. & Adrian, R.J. 2016 Large-scale thermal motions of turbulent Rayleigh–Bénard convection in a wide aspect-ratio cylindrical domain. Intl J. Heat Fluid Flow 61, 183–196, sI TSFP9 special issue.CrossRefGoogle Scholar
Schlüter, A., Lortz, D. & Busse, F.H. 1965 On the stability of steady finite amplitude convection. J. Fluid Mech. 23 (1), 129–124.CrossRefGoogle Scholar
Sreenivasan, K.R., Bershadski, A. & Niemela, J.J. 2002 Mean wind and its reversals in thermal convection. Phys. Rev. E 65, 056306.CrossRefGoogle ScholarPubMed
Stork, K. & Müller, U. 1975 Convection in boxes: an experimental investigation in vertical cylinders and annuli. J. Fluid Mech. 71, 231–240.CrossRefGoogle Scholar
Sugiyama, K., Ni, R., Stevens, R.J.A.M., Chan, T.S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.CrossRefGoogle ScholarPubMed
Threlfall, D.C. 1975 Free convection in low temperature gaseous helium. J. Fluid Mech. 67, 17–28.CrossRefGoogle Scholar
Vogt, T., Horn, S., Grannan, A.M. & Aurnou, J.M. 2018 Jump rope vortex in liquid metal convection. Proc. Natl Acad. Sci. USA 115 (50), 12674–12679.CrossRefGoogle ScholarPubMed
Wagner, S. & Shishkina, O. 2013 Aspect-ratio dependency of Rayleigh–Bénard convection in box-shaped containers. Phys. Fluids 25 (8), 085110.CrossRefGoogle Scholar
Wan, Z.-H., Wei, P., Verzicco, R., Lohse, D., Ahlers, G. & Stevens, R.J.A.M. 2019 Effect of sidewall on heat transfer and flow structure in Rayleigh–Bénard convection. J. Fluid Mech. 881, 218–243.CrossRefGoogle Scholar
Wang, Y., He, X.-Z. & Tong, P. 2019 Turbulent temperature fluctuations in a closed Rayleigh–Bénard convection cell. J. Fluid Mech. 874, 263–284.CrossRefGoogle Scholar
Wei, P. & Ahlers, G. 2016 On the nature of fluctuations in turbulent Rayleigh–Bénard convection at large Prandtl numbers. J. Fluid Mech. 802, 203–244.CrossRefGoogle Scholar
Weiss, S. & Ahlers, G. 2011 Turbulent Rayleigh–Bénard convection in a cylindrical container with aspect ratio $\gamma =0.50$and Prandtl number $Pr=4.38$. J. Fluid Mech. 676, 1–4.CrossRefGoogle Scholar
Weiss, S., Wei, P. & Ahlers, G. 2016 Heat-transport enhancement in rotating turbulent Rayleigh–Bénard convection. Phys. Rev. E 93, 043102.CrossRefGoogle ScholarPubMed
Xi, H.-D. & Xia, K.-Q. 2007 Cessations and reversals of the large-scale circulation in turbulent thermal convection. Phys. Rev. E 75, 066307.CrossRefGoogle ScholarPubMed
Xi, H.-D. & Xia, K.-Q. 2008 Flow mode transition in turbulent thermal convection. Phys. Fluids 20, 055104.CrossRefGoogle Scholar
Xi, H.-D., Zhang, Y.-B., Hao, J.-T. & Xia, K.-Q. 2016 Higher-order flow modes in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 805, 31–51.CrossRefGoogle Scholar
Xi, H.D., Zhou, Q. & Xia, K.Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73, 056312.CrossRefGoogle ScholarPubMed
Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102, 044503.CrossRefGoogle ScholarPubMed
Xie, Y.-C., Wei, P. & Xia, K.-Q. 2013 Dynamics of the large-scale circulation in high-Prandtl-number turbulent thermal convection. J. Fluid Mech. 717, 322–346.CrossRefGoogle Scholar
Yanagisawa, T., Yamagishi, Y., Hamano, Y., Tasaka, Y. & Takeda, Y. 2011 Spontaneous flow reversals in Rayleigh–Bénard convection of a liquid metal. Phys. Rev. E 83, 036307.CrossRefGoogle ScholarPubMed
Zhou, Q., Xi, H.-D., Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid Mech. 630 (-1), 367–390.CrossRefGoogle Scholar