Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T20:49:15.181Z Has data issue: false hasContentIssue false
  • English
  • Français

Péclet-number dependence of small-scale anisotropy of passive scalar fluctuations under a uniform mean gradient in isotropic turbulence

Published online by Cambridge University Press:  24 June 2020

Tatsuya Yasuda Open the ORCID record for Tatsuya Yasuda [Opens in a new window] ,
Toshiyuki Gotoh Open the ORCID record for Toshiyuki Gotoh [Opens in a new window] ,
Takeshi Watanabe Open the ORCID record for Takeshi Watanabe [Opens in a new window]  and
Izumi Saito Open the ORCID record for Izumi Saito [Opens in a new window]
Tatsuya Yasuda*
Affiliation:
Department of Physical Science and Engineering, Nagoya Institute of Technology, Gokiso-cho, Showa-ku, Nagoya, Aichi 466-8555, Japan
Toshiyuki Gotoh
Affiliation:
Department of Physical Science and Engineering, Nagoya Institute of Technology, Gokiso-cho, Showa-ku, Nagoya, Aichi 466-8555, Japan
Takeshi Watanabe
Affiliation:
Department of Physical Science and Engineering, Nagoya Institute of Technology, Gokiso-cho, Showa-ku, Nagoya, Aichi 466-8555, Japan
Izumi Saito
Affiliation:
Department of Physical Science and Engineering, Nagoya Institute of Technology, Gokiso-cho, Showa-ku, Nagoya, Aichi 466-8555, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

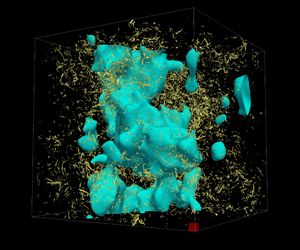
We study passive scalar fluctuations convected by statistically stationary homogeneous isotropic turbulence under a uniform mean scalar gradient. In order to elucidate the parameter dependence of small-scale statistics of scalar fluctuations, we conduct direct numerical simulations of passive scalar turbulence with 59 different combinations of Reynolds number and Schmidt number. For all the cases, we compute time-average statistics of various quantities, which include the scalar derivative skewness and flatness, the ratio of parallel-to-perpendicular scalar-gradient variances, and the anisotropy parameter recently proposed (Hill, Phys. Rev. Fluids, vol. 2, 2017, 094601). Notably, the degree of small-scale anisotropy of passive scalar fluctuation is characterised by a universal function of the Péclet number $Pe_{\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}}=u^{\prime }\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D705}$, where $u^{\prime }$ is the root mean square velocity, $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$ the Taylor microscale of scalar fluctuation, $\unicode[STIX]{x1D705}$ the mass diffusivity. In the definition of the Péclet number, the use of $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D703}}$, rather than the Taylor microscale of velocity fluctuation, is key to collapsing the data of different Reynolds and Schmidt numbers. When the Péclet number is low, large-scale anisotropic scalar structures emerge irrespective of the Reynolds number. These structures are elongated along the direction of the uniform mean scalar gradient, and their size is significantly larger than the integral length scale of velocity fluctuation.

JFM classification

Turbulent Flows: Turbulence theory Mixing: Turbulent mixing Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 898 , 10 September 2020 , A4
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.CrossRefGoogle Scholar
Batchelor, G. K., Howells, I. D. & Townsend, A. A. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 2. The case of large conductivity. J. Fluid Mech. 5, 134–139.CrossRefGoogle Scholar
Briard, A. & Gomez, T. 2016 Mixed-derivative skewness for high Prandtl and Reynolds numbers in homogeneous isotropic turbulence. Phys. Fluids 28, 081703.CrossRefGoogle Scholar
Budwig, R., Tavoularis, S. & Corrsin, S. 1985 Temperature fluctuations and heat flux in grid-generated isotropic turbulence with streamwise and transverse mean-temperature gradients. J. Fluid Mech. 153, 441–460.CrossRefGoogle Scholar
Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 22, 469–473.CrossRefGoogle Scholar
Donzis, D. A. & Yeung, P. K. 2010 Resolution effects and scaling in numerical simulations of passive scalar mixing in turbulence. Physica D 239, 1278–1287.Google Scholar
Eckert, E. R. G. & Drake, R. M. 1959 Heat and Mass Transfer, 2nd edn. McGraw-Hill Education.Google Scholar
Gotoh, T., Hatanaka, S. & Miura, H. 2012 Spectral compact difference hybrid computation of passive scalar in isotropic turbulence. J. Compt. Phys. 231, 7398–7414.CrossRefGoogle Scholar
Gotoh, T. & Watanabe, T. 2015 Power and nonpower laws of passive scalar moments convected by isotropic turbulence. Phys. Rev. Lett. 115, 114502.CrossRefGoogle ScholarPubMed
Gotoh, T., Watanabe, T. & Miura, H. 2014 Spectrum of passive scalar at very high Schmidt number in turbulence. Plasma Fusion Res. 9, 3401019.Google Scholar
Gotoh, T., Watanabe, T. & Suzuki, Y. 2011 Universality and anisotropy in passive scalar fluctuations in turbulence with uniform mean gradient. J. Turbul. 12, 1–27.Google Scholar
Gotoh, T. & Yeung, P. K. 2012 Passive scalar transport in turbulence: a computational perspective. In Ten Chapters in Turbulence (ed. Davidson, P. A., Kaneda, Y. & Sreenivasan, K. R.), pp. 87–131. Cambridge University Press.CrossRefGoogle Scholar
Hill, R. J. 2017 Spectra of turbulently advected scalars that have small Schmidt number. Phys. Rev. Fluids 2, 094601.CrossRefGoogle Scholar
Holzer, M. & Siggia, E. D. 1994 Turbulent mixing of a passive scalar. Phys. Fluids 6, 1820–1837.CrossRefGoogle Scholar
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.CrossRefGoogle Scholar
Lepore, J. & Mydlarski, L. 2012 Finite-Péclet-number effects on the scaling exponents of high-order passive scalar structure functions. J. Fluid Mech. 713, 453–481.CrossRefGoogle Scholar
Mydlarski, L. & Warhaft, Z. 1998 Passive scalar statistics in high-Péclet-number grid turbulence. J. Fluid Mech. 358, 135–175.CrossRefGoogle Scholar
Obukhov, A. M. 1949 Structure of the temperature field in turbulent flow. Izv. Akad. Nauk SSSR 13, 58–69.Google Scholar
O’Gorman, P. A. & Pullin, D. I. 2005 Effect of Schmidt number on the velocity-scalar cospectrum in isotropic turbulence with a mean scalar gradient. J. Fluid Mech. 532, 111–140.CrossRefGoogle Scholar
Schumacher, J., Sreenivasan, K. R. & Yeung, P. K. 2003 Schmidt number dependence of derivative moments for quasi-static straining motion. J. Fluid Mech. 479, 221–230.CrossRefGoogle Scholar
Schumacher, J., Sreenivasan, K. R. & Yeung, P. K. 2005 Very fine structures in scalar mixing. J. Fluid Mech. 531, 113–122.CrossRefGoogle Scholar
Sreenivasan, K. R. 1991 On local isotropy of passive scalars in turbulent shear flows. Proc. R. Soc. Lond. A 434, 165–182.Google Scholar
Sreenivasan, K. R. 1996 The passive scalar spectrum and the Obukhov–Corrsin constant. Phys. Fluids 8, 189–196.CrossRefGoogle Scholar
Sreenivasan, K. R. 2018 Turbulent mixing: a perspective. Proc. Natl Acad. Sci. USA 116, 18175–18183.CrossRefGoogle ScholarPubMed
Sreenivasan, K. R. & Tavoularis, S. 1980 On the skewness of the temperature derivative in turbulent flows. J. Fluid Mech. 101, 783–795.CrossRefGoogle Scholar
Tong, C. & Warhaft, Z. 1994 On passive scalar derivative statistics in grid turbulence. Phys. Fluids 6, 2165–2176.CrossRefGoogle Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.CrossRefGoogle Scholar
Watanabe, T. & Gotoh, T. 2004 Statistics of a passive scalar in homogeneous turbulence. New J. Phys. 6, 40.CrossRefGoogle Scholar
Watanabe, T. & Gotoh, T. 2007 Inertial-range intermittency and accuracy of direct numerical simulation for turbulence and passive scalar turbulence. J. Fluid Mech. 590, 117–146.CrossRefGoogle Scholar
Yeung, P. K., Donzis, D. A. & Sreenivasan, K. R. 2005 High-Reynolds-number simulation of turbulent mixing. Phys. Fluids 17, 081703.CrossRefGoogle Scholar
Yeung, P. K. & Sreenivasan, K. R. 2013 Spectrum of passive scalars of high molecular diffusivity in turbulent mixing. J. Fluid Mech. 716, R14.CrossRefGoogle Scholar
Yeung, P. K. & Sreenivasan, K. R. 2014 Direct numerical simulation of turbulent mixing at very low Schmidt number with a uniform mean gradient. Phys. Fluids 26, 015107.CrossRefGoogle Scholar
Yeung, P. K., Xu, S., Donzis, D. A. & Sreenivasan, K. R. 2004 Simulations of three-dimensional turbulent mixing for Schmidt numbers of the order 1000. Flow Turbul. Combust. 72, 333–347.CrossRefGoogle Scholar
Yeung, P. K., Xu, S. & Sreenivasan, K. R. 2002 Schmidt number effects on turbulent transport with uniform mean scalar gradient. Phys. Fluids 14, 4178–4191.CrossRefGoogle Scholar