Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Shtern, Vladimir
2014.
Moffatt eddies at an interface.
Theoretical and Computational Fluid Dynamics,
Vol. 28,
Issue. 6,
p.
651.
Balci, Adnan
Brøns, Morten
Herrada, Miguel A
and
Shtern, Vladimir N
2015.
Vortex breakdown in a truncated conical bioreactor.
Fluid Dynamics Research,
Vol. 47,
Issue. 6,
p.
065503.
Balci, Adnan
Brøns, Morten
Herrada, Miguel A.
and
Shtern, Vladimir N.
2016.
Bifurcations of a creeping air–water flow in a conical container.
Theoretical and Computational Fluid Dynamics,
Vol. 30,
Issue. 5,
p.
485.
Balci, Adnan
Brøns, Morten
Herrada, Miguel A.
and
Shtern, Vladimir N.
2016.
Patterns of a slow air–water flow in a semispherical container.
European Journal of Mechanics - B/Fluids,
Vol. 58,
Issue. ,
p.
1.
Carrión, Luis
Herrada, Miguel A.
and
Shtern, Vladimir N.
2017.
Topology changes in a water-oil swirling flow.
Physics of Fluids,
Vol. 29,
Issue. 3,
Naumov, I. V.
Sharifullin, B. R.
and
Shtern, V. N.
2017.
Capillary hysteresis in a confined swirling two-fluid flow.
Journal of Engineering Thermophysics,
Vol. 26,
Issue. 3,
p.
391.
Naumov, I.V.
Sharifullin, B.R.
and
Shtern, V.N.
2017.
Hysteresis in a swirling two-fluid flow.
Journal of Physics: Conference Series,
Vol. 899,
Issue. ,
p.
032015.
Carrión, Luis
Herrada, Miguel A.
and
Shtern, Vladimir N.
2017.
Topology and stability of a water-soybean-oil swirling flow.
Physical Review Fluids,
Vol. 2,
Issue. 2,
Carrión, Luis
Herrada, Miguel A
Shtern, Vladimir N
and
María López-Herrera, José
2017.
Patterns and stability of a whirlpool flow.
Fluid Dynamics Research,
Vol. 49,
Issue. 2,
p.
025519.
Carrión, Luis
Herrada, Miguel A.
and
Shtern, Vladimir N.
2018.
Stability of an air–water flow in a semispherical container.
European Journal of Mechanics - B/Fluids,
Vol. 67,
Issue. ,
p.
377.
Sharifullin, B R
Naumov, I V
Herrada, M A
and
Shtern, V N
2018.
Column formation and hysteresis in a two-fluid tornado.
Journal of Physics: Conference Series,
Vol. 980,
Issue. ,
p.
012008.
Naumov, Igor V.
Herrada, Miguel A.
Sharifullin, Bulat R.
and
Shtern, Vladimir N.
2018.
Slip at the interface of a two-fluid swirling flow.
Physics of Fluids,
Vol. 30,
Issue. 7,
Shtern, Vladimir
2018.
Mechanisms of jet instability: role of deceleration.
Fluid Dynamics Research,
Vol. 50,
Issue. 5,
p.
051408.
Naumov, Igor V.
Herrada, Miguel A.
Sharifullin, Bulat R.
and
Shtern, Vladimir N.
2018.
Hysteretic growth and decay of a waterspout column.
Physical Review Fluids,
Vol. 3,
Issue. 2,
Naumov, I V
Glavny, V G
Sharifullin, B R
and
Shtern, V N
2018.
Multi-cellular pattern of a two-fluid swirling flow in a closed cylinder.
Journal of Physics: Conference Series,
Vol. 1105,
Issue. ,
p.
012030.
Gulati, Shreyash
Riley, Frank P.
Lopez, Juan M.
and
Hirsa, Amir H.
2018.
Mixing within drops via surface shear viscosity.
International Journal of Heat and Mass Transfer,
Vol. 125,
Issue. ,
p.
559.
Naumov, Igor V.
Glavny, Vladimir G.
Sharifullin, Bulat R.
and
Shtern, Vladimir N.
2019.
Formation of a thin circulation layer in a two-fluid rotating flow.
Physical Review Fluids,
Vol. 4,
Issue. 5,
Naumov, Igor V.
Sharifullin, Bulat R.
Kravtsova, Aleksandra Yu.
and
Shtern, Vladimir N.
2020.
Velocity jumps and the Moffatt eddy in two-fluid swirling flows.
Experimental Thermal and Fluid Science,
Vol. 116,
Issue. ,
p.
110116.
Carrion, L.
Naumov, I. V.
Sharifullin, B. R.
Herrada, M. A.
and
Shtern, V. N.
2020.
Mechanism of Disappearance of Vortex Breakdown in a Confined Flow.
Journal of Engineering Thermophysics,
Vol. 29,
Issue. 1,
p.
49.
Naumov, I. V.
Sharifullin, B. R.
Herrada, M. A.
and
Shtern, V. N.
2023.
Effect of Rotation on Boundary Conditions at the Interface of Two Immiscible Fluids.
Journal of Engineering Thermophysics,
Vol. 32,
Issue. 3,
p.
508.
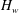 $H_{w}$ varies from 0 to 1. At
$H_{w}$ varies from 0 to 1. At 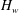 $H_{w}$ around 0.8, there are two large regions of the clockwise meridional circulation, one in air and one in water. These regions are separated by two small cells of the anticlockwise circulation adjacent to the interface near the sidewall in water and near the axis in air. The air cell is a thin layer and topologically is a bubble–ring for
$H_{w}$ around 0.8, there are two large regions of the clockwise meridional circulation, one in air and one in water. These regions are separated by two small cells of the anticlockwise circulation adjacent to the interface near the sidewall in water and near the axis in air. The air cell is a thin layer and topologically is a bubble–ring for 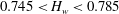 $0.745 < H_{w} < 0.785$. Alterations of this flow pattern are explored as (i) pressure increases, (ii) the bottom disk co-rotates and (iii) the top-disk rotation speeds up. This paper provides the physical reasoning behind the flow transformations; the results are of fundamental interest and can be utilized in bioreactors.
$0.745 < H_{w} < 0.785$. Alterations of this flow pattern are explored as (i) pressure increases, (ii) the bottom disk co-rotates and (iii) the top-disk rotation speeds up. This paper provides the physical reasoning behind the flow transformations; the results are of fundamental interest and can be utilized in bioreactors.