Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T06:57:24.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Pattern wavelengths and transport characteristics in three-dimensional bioconvection generated by chemotactic bacteria

Published online by Cambridge University Press:  22 November 2022

Hideki Yanaoka Open the ORCID record for Hideki Yanaoka [Opens in a new window]  and
Tomomu Nishimura
Hideki Yanaoka*
Affiliation:
Department of Systems Innovation Engineering, Faculty of Science and Engineering, Iwate University, 4-3-5 Ueda, Morioka, Iwate 020-8551, Japan
Tomomu Nishimura
Affiliation:
Kawasaki Heavy Industries, Ltd., 1-14-5 Kaigan, Minato-ku, Tokyo 105-8315, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

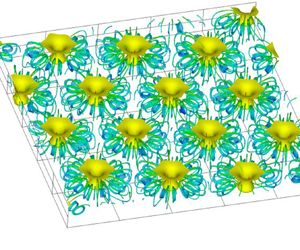
We conducted a three-dimensional numerical simulation of bioconvection generated by oxygen-reactive chemotactic bacteria. This study investigated the bioconvection patterns, interference between plumes, and the wavelength of bioconvection patterns. In addition, we clarified the transport characteristics of cells and oxygen in the bioconvection. Multiple plumes occur in the suspension, and three-dimensional bioconvection is formed around the plumes by the cells with vortex rings arising around the plumes. Even if bioconvection at a high Rayleigh number is disturbed, the bioconvection is strongly stable with respect to disturbances, and the pattern does not change due to disturbances. Bioconvection changes depending on the physical properties of bacteria and oxygen, and in particular, the rate of oxygen consumption by bacteria significantly affects the strength of bioconvection. Bioconvection patterns with different plume arrangements and shapes are formed for different Rayleigh numbers or initial disturbances of the cell concentration. As a result, the wavelengths of the patterns also vary. As the Rayleigh number increases, interference between plumes is strengthened by the shortening of the pattern wavelength, so the velocities of both upward and downward flows increase. Many cells are located under the plumes, and a strong shear flow occurs in these regions. As the pattern wavelength decreases, the cells are affected by high shear stress. Then the convective transport of the entire suspension strengthens and the transport characteristics of cells and oxygen improve. When the chamber boundary is changed to side walls, bacteria adhere to the wall surface, and plumes are arranged regularly along the side walls.

JFM classification

Biological Fluid Dynamics: Bioconvection Nonlinear Dynamical Systems: Pattern formation Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 952 , 10 December 2022 , A13
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amsden, A.A. & Harlow, F.H. 1970 A simplified MAC technique for incompressible fluid flow calculations. J. Comput. Phys. 6 (2), 322–325.CrossRefGoogle Scholar
Bees, M.A. & Croze, O.A. 2014 Mathematics for streamlined biofuel production from unicellular algae. Biofuels 5 (1), 53–65.CrossRefGoogle Scholar
Bees, M.A. & Hill, N.A. 1997 Wavelengths of bioconvection patterns. J. Expl Biol. 200 (10), 1515–1526.CrossRefGoogle ScholarPubMed
Berg, H.C. & Brown, D.A. 1972 Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature 239 (5374), 500–504.CrossRefGoogle ScholarPubMed
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.CrossRefGoogle Scholar
Chertock, A., Fellner, K., Kurganov, A., Lorz, A. & Markowich, P.A. 2012 Sinking, merging and stationary plumes in a coupled chemotaxis-fluid model: a high-resolution numerical approach. J. Fluid Mech. 694, 155–190.CrossRefGoogle Scholar
Cross, M.C. & Hohenberg, P.C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65 (3), 851–1112.CrossRefGoogle Scholar
Czirók, A., Jánosi, I.M. & Kessler, J.O. 2000 Bioconvective dynamics: dependence on organism behaviour. J. Expl Biol. 203 (21), 3345–3354.CrossRefGoogle ScholarPubMed
Geng, P. & Kuznetsov, A.V. 2005 Settling of bidispersed small solid particles in a dilute suspension containing gyrotactic micro-organisms. Intl J. Engng Sci. 43 (11–12), 992–1010.CrossRefGoogle Scholar
Ghorai, S. & Hill, N.A. 2000 Wavelengths of gyrotactic plumes in bioconvection. Bull. Math. Biol. 62 (3), 429–450.CrossRefGoogle ScholarPubMed
Ghorai, S. & Hill, N.A. 2002 Axisymmetric bioconvection in a cylinder. J. Theor. Biol. 219 (2), 137–152.CrossRefGoogle Scholar
Hart, A. & Edwards, C. 1987 Buoyant density fluctuations during the cell cycle of Bacillus subtilis. Arch. Microbiol. 147 (1), 68–72.CrossRefGoogle ScholarPubMed
Hillesdon, A.J. & Pedley, T.J. 1996 Bioconvection in suspensions of oxytactic bacteria: linear theory. J. Fluid Mech. 324, 223–259.CrossRefGoogle Scholar
Hillesdon, A.J., Pedley, T.J. & Kessler, J.O. 1995 The development of concentration gradients in a suspension of chemotactic bacteria. Bull. Math. Biol. 57 (344), 299–344.CrossRefGoogle Scholar
Hirooka, T. & Nagase, H. 2003 Biodegradation of endocrine disrupting chemicals and its application for bioremediation – utilization of photoautotrophic microorganisms. J. Environ. Biotechnol. 3 (1), 23–32.Google Scholar
Itoh, A., Toida, H. & Saotome, Y. 2001 Control of bioconvection and its application for mechanical system (1st report, basic effects of electrical field on bioconvection). JSME Intl J. 67 (662), 2449–2454.Google Scholar
Itoh, A., Toida, H. & Saotome, Y. 2006 Control of bioconvection and its application for mechanical system (2nd report, pitch optimization of electrodes array and driving of mechanical system by controlled bioconvection). JSME Intl J. 72 (716), 972–978.Google Scholar
Jánosi, I.M., Kessler, J.O. & Horváth, V.K. 1998 Onset of bioconvection in suspensions of Bacillus subtilis. Phys. Rev. E 58 (4), 4793–4800.CrossRefGoogle Scholar
Kage, A., Hosoya, C., Baba, S.A. & Mogami, Y. 2013 Drastic reorganization of bioconvection pattern of Chlamydomonas: quantitative analysis of the pattern transition response. J. Expl Biol. 216 (24), 4557–4566.Google ScholarPubMed
Karimi, A. & Paul, M.R. 2013 Bioconvection in spatially extended domains. Phys. Rev. E 87 (5), 053016.CrossRefGoogle ScholarPubMed
Khan, M., Salahuddin, T., Malik, M.Y., Alqarni, M.S. & Alqahtani, A.M. 2020 Numerical modeling and analysis of bioconvection on MHD flow due to an upper paraboloid surface of revolution. Physica A 553, 124231.CrossRefGoogle Scholar
Koschmieder, E.L. & Switzer, D.W. 1992 The wavenumbers of supercritical surface-tension-driven Bénard convection. J. Fluid Mech. 240, 533–548.CrossRefGoogle Scholar
Kuznetsov, A.V. 2005 The onset of bioconvection in a suspension of negatively geotactic microorganisms with high-frequency vertical vibration. Intl Commun. Heat Mass Transfer 32 (9), 1119–1127.CrossRefGoogle Scholar
Kuznetsov, A.V. 2011 Nanofluid bioconvection: interaction of microorganisms oxytactic upswimming, nanoparticle distribution, and heating/cooling from below. Theor. Comput. Fluid Dyn. 26, 291–310.CrossRefGoogle Scholar
Lee, H.G. & Kim, J. 2015 Numerical investigation of falling bacterial plumes caused by bioconvection in a three-dimensional chamber. Eur. J. Mech. (B/Fluids) 52, 120–130.CrossRefGoogle Scholar
Matsumoto, M. & Nishimura, T. 1998 Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul. 8 (1), 3–30.CrossRefGoogle Scholar
Mazzoni, S., Giavazzi, F., Cerbino, R., Giglio, M. & Vailati, A. 2008 Mutual Voronoi tessellation in spoke pattern convection. Phys. Rev. Lett. 100 (18), 188104.CrossRefGoogle ScholarPubMed
Metcalfe, A.M. & Pedley, T.J. 1998 Bacterial bioconvection: weakly nonlinear theory for pattern selection. J. Fluid Mech. 370, 249–270.CrossRefGoogle Scholar
Metcalfe, A.M. & Pedley, T.J. 2001 Falling plumes in bacterial bioconvection. J. Fluid Mech. 445, 121–149.CrossRefGoogle Scholar
Naseem, F., Shafiq, A., Zhao, L. & Naseem, A. 2017 MHD biconvective flow of Powell Eyring nanofluid over stretched surface. AIP Adv. 7, 065013.CrossRefGoogle Scholar
Noever, D.A. & Matsos, H.C. 1991 a A bioassay for monitoring cadmium based on bioconvective patterns. J. Environ. Sci. Heal. A 26 (2), 273–286.Google Scholar
Noever, D.A. & Matsos, H.C. 1991 b Calcium protection from cadmium poisoning: bioconvective indicators in Tetrahymena. J. Environ. Sci. Heal. A 26 (7), 1105–1113.Google Scholar
Noever, D.A., Matsos, H.C. & Looger, L.L. 1992 Bioconvective indicators in Tetrahymena: nickel and copper protection from cadmium poisoning. J. Environ. Sci. Heal. A 27 (2), 403–417.Google Scholar
Omori, T., Habe, H., Yoshida, T., Horinouchi, M., Saiki, Y. & Nojiri, H. 2003 Applied Ecological Microbiology. Shoko–do.Google Scholar
Omori, T., Nojiri, H., Horinouchi, M. & Kasuga, K. 2002 Environmental Biotechnology, 3rd edn. Shoko–do.Google Scholar
Pedley, T.J., Hill, N.A. & Kessler, J.O. 1988 The growth of bioconvection patterns in a uniform suspension of gyrotactic micro-organisms. J. Fluid Mech. 195, 223–237.CrossRefGoogle Scholar
Pedley, T.J. & Kessler, J.O. 1992 Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 24 (1), 313–358.CrossRefGoogle Scholar
Platt, J.R. 1961 Bioconvection patterns in cultures of free-swimming organisms. Science 133 (3466), 1766–1767.CrossRefGoogle ScholarPubMed
Shi, Q.-H., Hamid, A., Khan, M.I., Kumar, R.N., Gowda, R.J.P., Prasannakumara, B.C., Shah, N.A., Khan, S.U. & Chung, J.D. 2021 Numerical study of bio-convection flow of magneto-cross nanofluid containing gyrotactic microorganisms with activation energy. Sci. Rep. 11, 16030.CrossRefGoogle ScholarPubMed
Tomita, H. & Abe, K. 2000 Numerical simulation of pattern formation in the Bénard–Marangoni convection. Phys. Fluids 12 (6), 1389–1400.CrossRefGoogle Scholar
Tuval, I., Cisneros, L., Dombrowski, C., Wolgemuth, C.W., Kessler, J.O. & Goldstein, R.E. 2005 Bacterial swimming and oxygen transport near contact lines. Proc. Natl Acad. Sci. USA 102 (7), 2277–2282.CrossRefGoogle ScholarPubMed
Uddin, Md.J., Kabir, M.N. & Bég, O.A. 2016 Computational investigation of Stefan blowing and multiple-slip effects on buoyancy-driven bioconvection nanofluid flow with microorganisms. Intl J. Heat Mass Transfer 95, 116–130.CrossRefGoogle Scholar
Van der Pol, L. & Tramper, J. 1998 Shear sensitivity of animal cells from a culture-medium perspective. Trends Biotechnol. 16 (8), 323–328.CrossRefGoogle ScholarPubMed
Williams, C.R. & Bees, M.A. 2011 A tale of three taxes: photo-gyro-gravitactic bioconvection. J. Expl Biol. 214 (14), 2398–2408.CrossRefGoogle ScholarPubMed
Yamamoto, Y., Okayama, T., Sato, K. & Takaoki, T. 1992 Relation of pattern formation to external conditions in the flagellate, Chlamydomonas reinhardtii. Eur. J. Protistol. 28 (4), 415–420.CrossRefGoogle ScholarPubMed
Yanaoka, H., Inamura, T. & Suzuki, K. 2007 Numerical analysis of bioconvection generated by chemotactic bacteria. JSME Ser. B 73 (726), 575–580.CrossRefGoogle Scholar
Yanaoka, H., Inamura, T. & Suzuki, K. 2008 Three dimensional numerical analysis of bioconvection generated by chemotactic bacteria. JSME Ser. B 74 (737), 135–141.CrossRefGoogle Scholar
Zadeha, S.M.H., Mehryanb, S.A.M., Sheremetc, M.A., Izadid, M. & Ghodrate, M. 2020 Numerical study of mixed bio-convection associated with a micropolar fluid. Therm. Sci. Engng Prog. 18, 100539.Google Scholar