Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T14:51:49.379Z Has data issue: false hasContentIssue false
  • English
  • Français

Passive scalar transport in rotating turbulent channel flow

Published online by Cambridge University Press:  04 April 2018

Geert Brethouwer Open the ORCID record for Geert Brethouwer [Opens in a new window]
Get access Rights & Permissions [Opens in a new window]

Abstract

Passive scalar transport in turbulent channel flow subject to spanwise system rotation is studied by direct numerical simulations. The Reynolds number 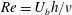$Re=U_{b}h/\unicode[STIX]{x1D708}$ is fixed at 20 000 and the rotation number 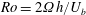$Ro=2\unicode[STIX]{x1D6FA}h/U_{b}$ is varied from 0 to 1.2, where 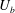$U_{b}$ is the bulk mean velocity, 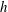$h$ the half channel gap width and 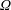$\unicode[STIX]{x1D6FA}$ the rotation rate. The scalar is constant but different at the two walls, leading to steady scalar transport across the channel. The rotation causes an unstable channel side with relatively strong turbulence and turbulent scalar transport, and a stable channel side with relatively weak turbulence or laminar-like flow, weak turbulent scalar transport but large scalar fluctuations and steep mean scalar gradients. The distinct turbulent–laminar patterns observed at certain 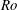$Ro$ on the stable channel side induce similar patterns in the scalar field. The main conclusions of the study are that rotation reduces the similarity between the scalar and velocity field and that the Reynolds analogy for scalar-momentum transport does not hold for rotating turbulent channel flow. This is shown by a reduced correlation between velocity and scalar fluctuations, and a strongly reduced turbulent Prandtl number of less than 0.2 on the unstable channel side away from the wall at higher 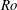$Ro$. On the unstable channel side, scalar scales become larger than turbulence scales according to spectra and the turbulent scalar flux vector becomes more aligned with the mean scalar gradient owing to rotation. Budgets in the governing equations of the scalar energy and scalar fluxes are presented and discussed as well as other statistics relevant for turbulence modelling.

JFM classification

Turbulent Flows: Rotating turbulence Turbulent Flows: Turbulence simulation Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 844 , 10 June 2018 , pp. 297 - 322
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H. & Antonia, R. A. 2009 Near-wall similarity between velocity and scalar fluctuations in turbulent channel flow. Phys. Fluids 21, 025109.10.1063/1.3081555Google Scholar
Abe, H. & Antonia, R. A. 2017 Relationship between the heat transfer law and the scalar dissipation function in a turbulent channel flow. J. Fluid Mech. 830, 300–325.10.1017/jfm.2017.564Google Scholar
Antonia, R. A., Abe, H. & Kawamura, H. 2009 Analogy between velocity and scalar fields in a turbulent channel flow. J. Fluid Mech. 628, 241–268.10.1017/S0022112009006181Google Scholar
Brethouwer, G. 2005 The effect of rotation on rapidly sheared homogeneous turbulence and passive scalar transport. J. Fluid Mech. 542, 305–342.10.1017/S0022112005006427Google Scholar
Brethouwer, G. 2016 Linear instabilities and recurring bursts of turbulence in rotating channel flow simulations. Phys. Rev. Fluids 1, 054404.10.1103/PhysRevFluids.1.054404Google Scholar
Brethouwer, G. 2017 Statistics and structure of spanwise rotating turbulent channel flow at moderate Reynolds numbers. J. Fluid Mech. 828, 424–458.10.1017/jfm.2017.526Google Scholar
Brethouwer, G., Duguet, Y. & Schlatter, P. 2012 Turbulent–laminar coexistence in wall flows with Coriolis, buoyancy or Lorentz forces. J. Fluid Mech. 704, 137–172.10.1017/jfm.2012.224Google Scholar
Brethouwer, G., Schlatter, P., Duguet, Y., Henningson, D. S. & Johansson, A. V. 2014 Recurrent bursts via linear processes in turbulent environments. Phys. Rev. Lett. 112, 144502.10.1103/PhysRevLett.112.144502Google Scholar
Chevalier, M., Schlatter, P., Lundbladh, A. & Henningson, D. S.2014 A pseudo-spectral solver for incompressible boundary layer flows. Technical Report TRITA-MEK 2007:07, KTH Mechanics, Stockholm, Sweden.Google Scholar
Dai, Y.-J., Huang, W.-X. & Xu, C.-X. 2016 Effects of Taylor–Görtler vortices on turbulent flows in a spanwise-rotating channel. Phys. Fluids 28, 115104.10.1063/1.4967702Google Scholar
Deusebio, E., Brethouwer, G., Schlatter, P. & Lindborg, E. 2014 A numerical study of the stratified and unstratified Ekman layer. J. Fluid Mech. 755, 672–704.10.1017/jfm.2014.318Google Scholar
Duguet, Y., Schlatter, P. & Henningson, D. S. 2010 Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 650, 119–129.10.1017/S0022112010000297Google Scholar
Grundestam, O., Wallin, S. & Johansson, A. V. 2008 Direct numerical simulations of rotating turbulent channel flow. J. Fluid Mech. 598, 177–199.10.1017/S0022112007000122Google Scholar
Hattori, H., Ohiwa, N., Kozuka, M. & Nagano, Y. 2009 Improvement of the nonlinear eddy diffusivity model for rotational turbulent heat transfer at various rotating axes. Fluid Dyn. Res. 41, 012402.10.1088/0169-5983/41/1/012402Google Scholar
Hsieh, A., Biringen, S. & Kucala, A. 2016 Simulation of rotating channel flow with heat transfer: evaluation of closure models. Trans. ASME J. Turbomach. 138, 111009.10.1115/1.4033463Google Scholar
Johansson, A. V. & Wikström, P. M. 1999 DNS and modelling of passive scalar transport in turbulent channel flow with a focus on scalar dissipation rate modelling. Flow Turbul. Combust. 63, 223–245.10.1023/A:1009948606944Google Scholar
Johnston, J. P., Halleen, R. M. & Lezius, D. K. 1972 Effects of spanwise rotation on the structure of two-dimensional fully developed turbulent channel flow. J. Fluid Mech. 56, 533–559.10.1017/S0022112072002502Google Scholar
Kassinos, S. C., Knaepen, B. & Carati, D. 2007 The transport of a passive scalar in magnetohydrodynamic turbulence subjected to mean shear and frame rotation. Phys. Fluids 19, 015105.10.1063/1.2409732Google Scholar
Kawamura, H., Abe, H. & Matsuo, Y. 1999 DNS of turbulent heat transfer in channel with respect to Reynolds and Prandtl number effects. Intl J. Heat Fluid Flow 20, 196–207.10.1016/S0142-727X(99)00014-4Google Scholar
Kawamura, H., Ohsaka, K., Abe, H. & Yamamoto, K. 1998 DNS of turbulent heat transfer in channel flow with low to medium-high Prandtl number fluid. Intl J. Heat Fluid Flow 19, 482–491.10.1016/S0142-727X(98)10026-7Google Scholar
Kristoffersen, R. & Andersson, H. I. 1993 Direct simulations of low-Reynolds number turbulent flow in a rotating channel. J. Fluid Mech. 256, 163–197.10.1017/S0022112093002757Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ∼ 5200. J. Fluid Mech. 774, 395–415.10.1017/jfm.2015.268Google Scholar
Liu, N.-S. & Lu, X.-Y. 2007 Direct numerical simulation of spanwise rotating turbulent channel flow with heat transfer. Intl J. Numer. Meth. Fluids 53, 1689–1706.10.1002/fld.1378Google Scholar
Matsubara, M. & Alfredsson, P. H. 1996 Experimental study of heat and momentum transfer in rotating channel flow. Phys. Fluids 8, 2964–2973.10.1063/1.869074Google Scholar
Müller, H., Younis, B. A. & Weigand, B. 2015 Development of a compact explicit algebraic model for the turbulent heat fluxes and its application in heated rotating flows. Intl J. Heat Mass Transfer 86, 880–889.10.1016/j.ijheatmasstransfer.2015.03.059Google Scholar
Nagano, Y. & Hattori, H. 2003 Direct numerical simulation and modelling of spanwise rotating channel flow with heat transfer. J. Turbul. 4, 010.10.1088/1468-5248/4/1/010Google Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2016 Passive scalars in turbulent channel flow at high Reynolds number. J. Fluid Mech. 788, 614–639.10.1017/jfm.2015.711Google Scholar
Wallin, S., Grundestam, O. & Johansson, A. V. 2013 Laminarization mechanisms and extreme-amplitude states in rapidly rotating plane channel flow. J. Fluid Mech. 730, 193–219.10.1017/jfm.2013.300Google Scholar
Wikström, P. M., Wallin, S. & Johansson, A. V. 2000 Derivation and investigation of a new explicit algebraic model for the passive scalar flux. Phys. Fluids 12, 688–702.10.1063/1.870274Google Scholar
Wu, H. & Kasagi, N. 2004 Turbulent heat transfer in a channel with arbitrary directional system rotation. Intl J. Heat Mass Transfer 47, 4579–4591.10.1016/j.ijheatmasstransfer.2003.07.034Google Scholar
Xia, Z., Shi, Y. & Chen, S. 2016 Direct numerical of turbulent channel flow with spanwise rotation. J. Fluid Mech. 788, 42–56.10.1017/jfm.2015.717Google Scholar
Yang, Y.-T. & Wu, J.-Z. 2012 Channel turbulence with spanwise rotation studied using helical wave decomposition. J. Fluid Mech. 692, 137–152.10.1017/jfm.2011.500Google Scholar
Yang, Z., Cui, G., Xu, C. & Zhang, Z. 2011 Study on the analogy between velocity and temperature fluctuations in the turbulent rotating channel flows. J. Phys.: Conf. Ser. 318, 022008.Google Scholar