Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T12:39:58.293Z Has data issue: false hasContentIssue false
  • English
  • Français

Passive pitching of splitters in the trailing edge of elliptic cylinders

Published online by Cambridge University Press:  03 August 2017

Y. Jin  and
L. P. Chamorro Open the ORCID record for L. P. Chamorro [Opens in a new window]
Y. Jin
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA
L. P. Chamorro*
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA Civil and Environmental Engineering Department, University of Illinois, Urbana, IL 61801, USA Aerospace Engineering Department, University of Illinois, Urbana, IL 61801, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The distinctive pitching of hinged splitters in the trailing edge of elliptic cylinders was experimentally studied at various angles of attack (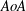$AoA$) of the cylinder, Reynolds numbers, splitter lengths, aspect ratios (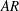$AR$) of the cylinder and freestream turbulence levels. High-resolution telemetry and hotwire anemometry were used to characterize and gain insight on the dynamics of splitters and wake flow. Results show that the motions of the splitters contain various dominating modes, e.g. 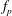$f_{p}$ and 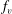$f_{v}$, which are induced by the mean flow and wake dynamics. High background turbulence dampens the coherence of the regular vortex shedding leading to negligible 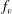$f_{v}$. For a sufficiently long splitter, namely twice the semimajor axis of the cylinder, dual vortex shedding mode exists close to the leading and trailing edges of the splitter. In general, the splitters oscillate around an equilibrium position nearly parallel to the mean direction of the flow; however, a skewed equilibrium is also possible with a strong recirculation region. This is the case with cylinders of low 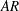$AR$ and high 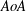$AoA$, where higher lift and drag occurs. Flow measurements at various transverse locations within the wake of the cylinder–splitter system indicate that the signature of the low-frequency splitter pitching is shifted in the wake in the cases with non-zero 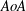$AoA$ of the cylinder. Although the splitter pitching exhibits two dominant vortex shedding modes in various configurations, only the higher frequency is transmitted to the wake.

JFM classification

Aerodynamics: Aerodynamics Aerodynamics: Flow-structure interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 363 - 375
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Allen, J. J. & Smits, A. J. 2001 Energy harvesting eel. J. Fluids Struct. 15 (3–4), 629–640.CrossRefGoogle Scholar
Apelt, C. J. & West, G. S. 1975 The effects of wake splitter plates on bluff-body flow in the range 104 < R < 5 × 104 . Part 2. J. Fluid Mech. 71 (01), 145–160.CrossRefGoogle Scholar
Argentina, M. & Mahadevan, L. 2005 Fluid-flow-induced flutter of a flag. Proc. Natl Acad. Sci. USA 102 (6), 1829–1834.CrossRefGoogle ScholarPubMed
Assi, G. R., Bearman, P. W. & Kitney, N. 2009 Low drag solutions for suppressing vortex-induced vibration of circular cylinders. J. Fluids Struct. 25 (4), 666–675.CrossRefGoogle Scholar
Bao, Y. & Tao, J. 2013 The passive control of wake flow behind a circular cylinder by parallel dual plates. J. Fluids Struct. 37, 201–219.CrossRefGoogle Scholar
Dudley, R., King, V. A. & Wassersug, R. J. 1991 The implications of shape and metamorphosis for drag forces on a generalized pond tadpole (rana catesbeiana). Copeia 1991 (1), 252–257.CrossRefGoogle Scholar
Eloy, C., Lagrange, R., Souilliez, C. & Schouveiler, L. 2008 Aeroelastic instability of cantilevered flexible plates in uniform flow. J. Fluid Mech. 611, 97–106.CrossRefGoogle Scholar
Gu, F., Wang, J. S., Qiao, X. Q. & Huang, Z. 2012 Pressure distribution, fluctuating forces and vortex shedding behavior of circular cylinder with rotatable splitter plates. J. Fluids Struct. 28, 263–278.CrossRefGoogle Scholar
Hamed, A. M., Vega, J., Liu, B. & Chamorro, L. P. 2017 Flow around a semicircular cylinder with passive flow control mechanisms. Exp. Fluids 58 (3), 22.CrossRefGoogle Scholar
Irwin, P. A. 2008 Bluff body aerodynamics in wind engineering. J. Wind Engng Ind. Aerodyn. 96 (6), 701–712.CrossRefGoogle Scholar
Jin, Y., Ji, S. & Chamorro, L. P. 2016a Spectral energy cascade of body rotations and oscillations under turbulence. Phys. Rev. E 94 (6), 063105.Google ScholarPubMed
Jin, Y., Ji, S., Liu, B. & Chamorro, L. P. 2016b On the role of thickness ratio and location of axis of rotation in the flat plate motions. J. Fluids Struct. 64, 127–137.CrossRefGoogle Scholar
Jin, Y., Liu, H., Aggarwal, R., Singh, A. & Chamorro, L. P. 2016c Effects of freestream turbulence in a model wind turbine wake. Energy 9 (10), 830.Google Scholar
Knisely, C. W. 1990 Strouhal numbers of rectangular cylinders at incidence: a review and new data. J. Fluids Struct. 4 (4), 371–393.CrossRefGoogle Scholar
Lācis, U., Brosse, N., Ingremeau, F., Mazzino, A., Lundell, F., Kellay, H. & Bagheri, S. 2014 Passive appendages generate drift through symmetry breaking. Nature Commun. 5, 5310.CrossRefGoogle ScholarPubMed
Laneville, A. & Yong, L. 1983 Mean flow patterns around two-dimensional rectangular cylinders and their interpretation. J. Wind Engng Ind. Aerodyn. 14 (1–3), 387–398.CrossRefGoogle Scholar
Liu, B., Hamed, A. M., Jin, Y. & Chamorro, L. P. 2017 Influence of vortical structure impingement on the oscillation and rotation of flat plates. J. Fluids Struct. 70, 417–427.CrossRefGoogle Scholar
Lu, L., Guo, X. L., Tang, G. Q., Liu, M. M., Chen, C. Q. & Xie, Z. H. 2016 Numerical investigation of flow-induced rotary oscillation of circular cylinder with rigid splitter plate. Phys. Fluids 28 (9), 093604.CrossRefGoogle Scholar
Modi, V. J., Wiland, E., Dikshit, A. K. & Yokomizo, T. 1992 On the fluid dynamics of elliptic cylinders. In The Second International Offshore and Polar Engineering Conference, International Society of Offshore and Polar Engineers.Google Scholar
Naimul Haque, M., Katsuchi, H., Yamada, H. & Nishio, M. 2014 Investigation of flow fields around rectangular cylinder under turbulent flow by les. Engng Appl. Comput. Fluids 8 (3), 396–406.Google Scholar
Nair, M. T. & Sengupta, T. K. 1997 Unsteady flow past elliptic cylinders. J. Fluids Struct. 11 (6), 555–595.CrossRefGoogle Scholar
Ozono, S. 1999 Flow control of vortex shedding by a short splitter plate asymmetrically arranged downstream of a cylinder. Phys. Fluids 11 (10), 2928–2934.CrossRefGoogle Scholar
Pastò, S. 2008 Vortex-induced vibrations of a circular cylinder in laminar and turbulent flows. J. Fluids Struct. 24 (7), 977–993.CrossRefGoogle Scholar
Paul, I., Arul Prakash, K. & Vengadesan, S. 2014 Numerical analysis of laminar fluid flow characteristics past an elliptic cylinder: a parametric study. Intl J. Numer. Meth. H 24 (7), 1570–1594.Google Scholar
Roshko, A. 1955 On the wake and drag of bluff bodies. J. Aero. Sci. 22, 124–132.CrossRefGoogle Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.CrossRefGoogle Scholar
Shukla, S., Govardhan, R. N. & Arakeri, J. H. 2009 Flow over a cylinder with a hinged-splitter plate. J. Fluids Struct. 25 (4), 713–720.CrossRefGoogle Scholar
Sudhakar, Y. & Vengadesan, S. 2012 Vortex shedding characteristics of a circular cylinder with an oscillating wake splitter plate. Comput. Fluids 53, 40–52.CrossRefGoogle Scholar
Tamura, T. & Miyagi, T. 1999 The effect of turbulence on aerodynamic forces on a square cylinder with various corner shapes. J. Wind Engng Ind. Aerodyn. 83 (1), 135–145.CrossRefGoogle Scholar
Thompson, M. C., Radi, A., Rao, A., Sheridan, J. & Hourigan, K. 2014 Low-Reynolds-number wakes of elliptical cylinders: from the circular cylinder to the normal flat plate. J. Fluid Mech. 751, 570–600.CrossRefGoogle Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36 (1), 413–455.CrossRefGoogle Scholar
Wu, X., Ge, F. & Hong, Y. 2012 A review of recent studies on vortex-induced vibrations of long slender cylinders. J. Fluids Struct. 28, 292–308.CrossRefGoogle Scholar
Yu, D., Butler, K., Kareem, A., Glimm, J. & Sun, J. 2012 Simulation of the influence of aspect ratio on the aerodynamics of rectangular prisms. J. Engng Mech. ASCE 139 (4), 429–438.CrossRefGoogle Scholar