Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2025-01-03T12:29:27.731Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle transport in turbulent curved pipe flow

Published online by Cambridge University Press:  15 March 2016

Azad Noorani ,
Gaetano Sardina ,
Luca Brandt  and
Philipp Schlatter
Azad Noorani*
Affiliation:
Swedish e-Science Research Centre (SeRC), Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
Gaetano Sardina
Affiliation:
Swedish e-Science Research Centre (SeRC), Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
Luca Brandt
Affiliation:
Swedish e-Science Research Centre (SeRC), Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
Philipp Schlatter
Affiliation:
Swedish e-Science Research Centre (SeRC), Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations (DNS) of particle-laden turbulent flow in straight, mildly curved and strongly bent pipes are performed in which the solid phase is modelled as small heavy spherical particles. A total of seven populations of dilute particles with different Stokes numbers, one-way coupled with their carrier phase, are simulated. The objective is to examine the effect of the curvature on micro-particle transport and accumulation. 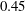It is shown that even a slight non-zero curvature in the flow configuration strongly impact the particle concentration map such that the concentration of inertial particles with bulk Stokes number $0.45$ (based on bulk velocity and pipe radius) at the inner bend wall of mildly curved pipe becomes 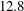$12.8$ times larger than that in the viscous sublayer of the straight pipe. Near-wall helicoidal particle streaks are observed in the curved configurations with their inclination varying with the strength of the secondary motion of the carrier phase. A reflection layer, as previously observed in particle laden turbulent S-shaped channels, is also apparent in the strongly curved pipe with heavy particles. In addition, depending on the curvature, the central regions of the mean Dean vortices appear to be completely depleted of particles, as observed also in the partially relaminarised region at the inner bend. The turbophoretic drift of the particles is shown to be affected by weak and strong secondary motions of the carrier phase and geometry-induced centrifugal forces. The first- and second-order moments of the velocity and acceleration of the particulate phase in the same configurations are addressed in a companion paper by the same authors. The current data set will be useful for modelling particles advected in wall-bounded turbulent flows where the effects of the curvature are not negligible.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 793 , 25 April 2016 , pp. 248 - 279
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.CrossRefGoogle Scholar
Berger, S. A., Talbot, L. & Yao, L. S. 1983 Flow in curved pipes. Annu. Rev. Fluid Mech. 15 (1), 461–512.Google Scholar
Berrouk, A. S. & Laurence, D. 2008 Stochastic modelling of aerosol deposition for les of $90^{\circ }$ degree bend turbulent flow. Intl J. Heat Fluid Flow 29 (4), 1010–1028.Google Scholar
Boersma, B. J. & Nieuwstadt, F. T. M. 1996 Large-eddy simulation of turbulent flow in a curved pipe. Trans. ASME J. Fluids Engng 118 (2), 248–254.CrossRefGoogle Scholar
Bradshaw, P. 1987 Turbulent secondary flows. Annu. Rev. Fluid Mech. 19, 53–74.Google Scholar
Breuer, M., Baytekin, H. T. & Matida, E. A. 2006 Prediction of aerosol deposition in $90^{\circ }$ bends using les and an efficient lagrangian tracking method. J. Aerosol Sci. 37 (11), 1407–1428.Google Scholar
Caporaloni, M., Tampieri, F., Trombetti, F. & Vittori, O. 1975 Transfer of particles in nonisotropic air turbulence. J. Atmos. Sci. 32, 565–568.2.0.CO;2>CrossRefGoogle Scholar
Chevalier, M., Schlatter, P., Lundbladh, A. & Henningson, D. S.2007 simson – a pseudo-spectral solver for incompressible boundary layer flows. Tech. Rep. TRITA-MEK 2007:07, KTH Mechanics, Stockholm, Sweden.Google Scholar
Chin, C., Ooi, A., Marusic, I. & Blackburn, H. M. 2010 The influence of pipe length on turbulence statistics computed from direct numerical simulation data. Phys. Fluids 22 (11), 115107.Google Scholar
Coleman, S. W. & Vassilicos, J. C. 2009 A unified sweep-stick mechanism to explain particle clustering in two-and three-dimensional homogeneous, isotropic turbulence. Phys. Fluids 21, 113301.Google Scholar
Crowe, C. T., Schwarzkopf, J. D., Sommerfeld, M. & Tsuji, Y. 2011 Multiphase Flows with Droplets and Particles, 2nd edn. CRC Press.CrossRefGoogle Scholar
Edwards, J. K., McLaury, B. S. & Shirazi, S. A. 2001 Modeling solid particle erosion in elbows and plugged tees. J. Energy Resour. Technol. 123 (4), 277–284.CrossRefGoogle Scholar
Elghobashi, S. 1991 Particle-laden turbulent flows: direct simulation and closure models. Appl. Sci. Res. 48 (3–4), 301–314.Google Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52 (4), 309–329.Google Scholar
Elghobashi, S. & Truesdell, G. C. 1992 Direct simulation of particle dispersion in a decaying isotropic turbulence. J. Fluid Mech. 242 (3), 655–700.CrossRefGoogle Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 nek5000 Web page.http://nek5000.mcs.anl.gov.Google Scholar
Germano, M. 1982 On the effect of torsion on a helical pipe flow. J. Fluid Mech. 125 (1), 1–8.CrossRefGoogle Scholar
Goto, S. & Vassilicos, J. C. 2008 Sweep-stick mechanism of heavy particle clustering in fluid turbulence. Phys. Rev. Lett. 100 (5).Google Scholar
van Hinsberg, M. A. T., ten Thije Boonkkamp, J. H. M., Toschi, F. & Clercx, H. J. H. 2013 Optimal interpolation schemes for particle tracking in turbulence. Phys. Rev. E 87 (4).CrossRefGoogle ScholarPubMed
Huang, X. & Durbin, P. 2010 Particulate dispersion in a turbulent serpentine channel. Flow Turbul. Combust. 85 (3–4), 333–344.Google Scholar
Huang, X. & Durbin, P. 2012 Particulate mixing in a turbulent serpentine duct. Phys. Fluids 24.CrossRefGoogle Scholar
Hüttl, T. J. & Friedrich, R. 2000 Influence of curvature and torsion on turbulent flow in helically coiled pipes. Intl J. Heat Fluid Flow 21 (3), 345–353.Google Scholar
Ito, H. 1959 Friction factors for turbulent flow in curved pipes. Trans. ASME J. Basic Engng 81 (2), 123–134.CrossRefGoogle Scholar
Kaftori, D., Hetsroni, G. & Banerjee, S. 1995a Particle behavior in the turbulent boundary layer. I. Motion, deposition, and entrainment. Phys. Fluids 7.Google Scholar
Kaftori, D., Hetsroni, G. & Banerjee, S. 1995b Particle behavior in the turbulent boundary layer. II. Velocity and distribution profiles. Phys. Fluids 7.Google Scholar
Kalpakli, A. & Örlü, R. 2013 Turbulent pipe flow downstream a $90^{\circ }$ pipe bend with and without superimposed swirl. Intl J. Heat Fluid Flow 41, 103–111.Google Scholar
Li, Y., McLaughlin, J. B., Kontomaris, K. & Portela, L. 2001 Numerical simulation of particle-laden turbulent channel flow. Phys. Fluids 13, 29–57.CrossRefGoogle Scholar
Manlapaz, R. L. & Churchill, S. W. 1981 Fully developed laminar convection from a helical coil. Chem. Engng Commun. 9 (1–6), 185–200.Google Scholar
Marchioli, C. & Soldati, A. 2002 Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 468, 283–315.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.Google Scholar
Mehlig, B., Wilkinson, M., Duncan, K., Weber, T. & Ljunggren, M. 2005 Aggregation of inertial particles in random flows. Phys. Rev. E 72 (5).CrossRefGoogle ScholarPubMed
Milici, B., De Marchis, M., Sardina, G. & Napoli, E. 2014 Effects of roughness on particle dynamics in turbulent channel flows: a DNS analysis. J. Fluid Mech. 739 (1), 465–478.Google Scholar
Ninto, Y. & Garcia, M. H. 1996 Experiments on particle turbulence interactions in the near–wall region of an open channel flow: Implications for sediment transport. J. Fluid Mech. 326 (1), 285–319.Google Scholar
Noorani, A., El Khoury, G. K. & Schlatter, P. 2013 Evolution of turbulence characteristics from straight to curved pipes. Intl J. Heat Fluid Flow 41, 16–26.Google Scholar
Noorani, A., Sardina, G., Brandt, L. & Schlatter, P. 2015 Particle velocity and acceleration in turbulent bent pipe flows. Flow Turbul. Combust. 95 (2–3), 539–559.Google Scholar
Nowbahar, A., Sardina, G., Picano, F. & Brandt, L. 2013 Turbophoresis attenuation in a turbulent channel flow with polymer additives. J. Fluid Mech. 732, 706–719.Google Scholar
Picano, F., Sardina, G. & Casciola, C. M. 2009 Spatial development of particle-laden turbulent pipe flow. Phys. Fluids 21.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Reeks, M. W. 1983 The transport of discrete particles in inhomogeneous turbulence. J. Aerosol Sci. 14 (6), 729–739.CrossRefGoogle Scholar
Rouson, D. W. I. & Eaton, J. K. 2001 On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 428 (1), 149–169.Google Scholar
Sardina, G., Schlatter, P., Brandt, L., Picano, F. & Casciola, C. M. 2012a Wall accumulation and spatial localization in particle-laden wall flows. J. Fluid Mech. 699, 50–78.Google Scholar
Sardina, G., Schlatter, P., Picano, F., Casciola, C. M., Brandt, L. & Henningson, D. S. 2012b Self-similar transport of inertial particles in a turbulent boundary layer. J. Fluid Mech. 706, 584–596.Google Scholar
Schiller, L. & Naumann, A. 1933 Über die grundlegenden berechnungen bei der schwerkraftaufbereitung. Ver. Deut. Ing. 77, 318–320.Google Scholar
Sikovsky, D. Ph. 2014 Singularity of inertial particle concentration in the viscous sublayer of wall-bounded turbulent flows. Flow Turbul. Combust. 92 (1–2), 41–64.Google Scholar
Soldati, A. & Marchioli, C. 2009 Physics and modelling of turbulent particle deposition and entrainment: review of a systematic study. Intl J. Multiphase Flow 35 (9), 827–839.Google Scholar
Squires, K. D. & Eaton, J. K. 1991 Measurements of particle dispersion obtained from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 226, 1–35.Google Scholar
Tomboulides, A. G., Lee, J. C. Y. & Orszag, S. A. 1997 Numerical simulation of low Mach number reactive flows. J. Sci. Comput. 12 (2), 139–167.CrossRefGoogle Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.Google Scholar
Vashisth, S., Kumar, V. & Nigam, K. 2008 A review on the potential applications of curved geometries in process industry. Ind. Engng Chem. Res. 47 (10), 3291–3337.Google Scholar
Wang, L. P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar
Winzeler, H. B. & Belfort, G. 1993 Enhanced performance for pressure-driven membrane processes: the argument for fluid instabilities. J. Membr. Sci. 80 (1), 35–47.Google Scholar
Wu, Z. & Young, J. B. 2012 The deposition of small particles from a turbulent air flow in a curved duct. Intl J. Multiphase Flow 44, 34–47.Google Scholar
Young, J. & Leeming, A. 1997 A theory of particle deposition in turbulent pipe flow. J. Fluid Mech. 340 (1), 129–159.CrossRefGoogle Scholar
Zonta, F., Marchioli, C. & Soldati, A. 2013 Particle and droplet deposition in turbulent swirled pipe flow. Intl J. Multiphase Flow 56, 172–183.Google Scholar