Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T13:32:17.917Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle saltation over rigid bumpy beds in viscous shearing flows

Published online by Cambridge University Press:  25 August 2022

Alexandre Valance Open the ORCID record for Alexandre Valance [Opens in a new window]  and
Diego Berzi Open the ORCID record for Diego Berzi [Opens in a new window]
Alexandre Valance*
Affiliation:
Institut de Physique de Rennes, Université de Rennes 1, Campus Beaulieu, 35 042 Rennes Cedex, France
Diego Berzi
Affiliation:
Department of Civil and Environmental Engineering, Politecnico di Milano, 20133 Milano, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

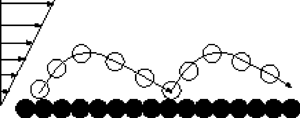
We investigate the steady motion of solid particles through successive jumps over a horizontal, rigid, bumpy bed driven by the shearing of a viscous fluid in the absence of turbulence, lubrication forces and collisions above the bed. We employ a discrete element method for the particles coupled to a mean field continuum model for the fluid to run quasi-two-dimensional simulations that we compare with the predictions of a simple model which assumes that all the particles follow identical periodic trajectories determined by the intensity of the shearing and compatible with previously suggested laws relating the particle velocities before and after the impact with the bed. We solve the periodic model both numerically and analytically, and identify the solutions that are linearly stable to small perturbations. We show that the stable solutions of the periodic model are in qualitative and quantitative agreement with the discrete simulations, as long as the number of moving particles in the system is not too large. The discrete simulations further reveal that there are two distinct families of particle trajectories, and that the simple periodic model is actually a good representation of the more energetic particles, that spend most of their time in the upper flow layers where they can gain momentum from the flow.

JFM classification

Geophysical and Geological Flows: Sediment transport Low-Reynolds-number flows: Stokesian dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 947 , 25 September 2022 , A28
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abbott, J.E. & Francis, J.R.D. 1977 Saltation and suspension trajectories of solid grains in a water stream. Phil. Trans. R. Soc. A 284 (1321), 225–254.Google Scholar
Ancey, C., Bigillon, F., Frey, P., Lanier, J. & Ducret, R. 2002 Saltating motion of a bead in a rapid water stream. Phys. Rev. E 66 (3), 036306.CrossRefGoogle Scholar
Andreotti, B. 2004 A two-species model of aeolian sand transport. J. Fluid Mech. 510, 47–70.CrossRefGoogle Scholar
Aussillous, P., Chauchat, J., Pailha, M., Médale, M. & Guazzelli, É. 2013 Investigation of the mobile granular layer in bedload transport by laminar shearing flows. J. Fluid Mech. 736, 594–615.CrossRefGoogle Scholar
Bagnold, R.A. 1941 The Physics of Blown Sand and Desert Dunes. Methuen.Google Scholar
Beladjine, D., Ammi, M., Oger, L. & Valance, A. 2007 Collision process between an incident bead and a three-dimensional granular packing. Phys. Rev. E 75 (6), 061305.CrossRefGoogle Scholar
Berzi, D., Jenkins, J.T. & Valance, A. 2016 Periodic saltation over hydrodynamically rough beds: aeolian to aquatic. J. Fluid Mech. 786, 190–209.CrossRefGoogle Scholar
Berzi, D., Valance, A. & Jenkins, J.T. 2017 The threshold for continuing saltation on earth and other solar system bodies. J. Geophys. Res. 122 (7), 1374–1388.CrossRefGoogle Scholar
Burr, D.M., Bridges, N.T., Marshall, J.R., Smith, J.K., White, B.R. & Emery, J.P. 2015 Higher-than-predicted saltation threshold wind speeds on Titan. Nature 517, 60–63.CrossRefGoogle ScholarPubMed
Charru, F., Andreotti, B. & Claudin, P. 2013 Sand ripples and dunes. Annu. Rev. Fluid Mech. 45 (1), 469–493.CrossRefGoogle Scholar
Charru, F., Larrieu, E., Dupont, J.B. & Zenit, R. 2007 Motion of a particle near a rough wall in a viscous shear flow. J. Fluid Mech. 570, 431–453.CrossRefGoogle Scholar
Charru, F. & Mouilleron-Arnould, H. 2002 Instability of a bed of particles sheared by a viscous flow. J. Fluid Mech. 452, 303–323.CrossRefGoogle Scholar
Crassous, J., Beladjine, D. & Valance, A. 2007 Impact of a projectile on a granular medium described by a collision model. Phys. Rev. Lett. 99 (24), 248001.CrossRefGoogle ScholarPubMed
Creyssels, M., Dupont, P., El Moctar, A.O., Valance, A., Cantat, I., Jenkins, J.T., Pasini, J.M. & Rasmussen, K.R. 2009 Saltating particles in a turbulent boundary layer: experiment and theory. J. Fluid Mech. 625, 47–74.CrossRefGoogle Scholar
Dall'Acqua, D., Benucci, M., Corvaro, F., Leporini, M., Cocci Grifoni, R., Del Monaco, A., Di Lullo, A., Passucci, C. & Marchetti, B. 2017 Experimental results of pipeline dewatering through surfactant injection. J. Petrol. Sci. Engng 159 (September), 542–552.CrossRefGoogle Scholar
Durán, O., Andreotti, B. & Claudin, P. 2012 Numerical simulation of turbulent sediment transport. From bed load to saltation. Phys. Fluids 24, 103306.CrossRefGoogle Scholar
Durán, O., Claudin, P. & Andreotti, B. 2011 On aeolian transport: grain-scale interactions, dynamical mechanisms and scaling laws. Aeolian Res. 3 (3), 243–270.CrossRefGoogle Scholar
Fernandez Luque, R. & Van Beek, R. 1976 Erosion and transport of bed-load sediment. J. Hydraul. Res. 14 (2), 127–144.CrossRefGoogle Scholar
Greeley, R., Iversen, J., Leach, R., Marshall, J., Williams, S. & White, B. 1984 Windblown sand on Venus - preliminary results of laboratory simulations. Icarus 57, 112–124.CrossRefGoogle Scholar
Ho, T.D., Valance, A., Dupont, P. & Ould El Moctar, A. 2014 Aeolian sand transport: length and height distributions of saltation trajectories. Aeolian Res. 12, 65–74.CrossRefGoogle Scholar
Iversen, J.D., Pollack, J.B., Greeley, R. & White, B.R. 1976 Saltation threshold on Mars: the effect of interparticle force, surface roughness, and low atmospheric density. Icarus 29 (3), 381–393.CrossRefGoogle Scholar
Iversen, J.D. & Rasmussen, K.R. 1999 The effect of wind speed and bed slope on sand transport. Sedimentology 46, 723–731.CrossRefGoogle Scholar
Iversen, J.D. & White, B.R. 1982 Saltation threshold on Earth, Mars and Venus. Sedimentology 29, 111–119.CrossRefGoogle Scholar
Jenkins, J.T. & Hanes, D.M. 1998 Collisional sheet flows of sediment driven by a turbulent fluid. J. Fluid Mech. 370, 29–52.CrossRefGoogle Scholar
Jenkins, J.T. & Valance, A. 2014 Periodic trajectories in aeolian sand transport. Phys. Fluids 26 (7), 073301.CrossRefGoogle Scholar
Kok, J.F., Parteli, E.J.R., Michaels, T.I. & Karam, D.B. 2012 The physics of wind-blown sand and dust. Rep. Prog. Phys. 75 (10), 106901.CrossRefGoogle Scholar
Leporini, M., Terenzi, A., Marchetti, B., Corvaro, F. & Polonara, F. 2019 On the numerical simulation of sand transport in liquid and multiphase pipelines. J. Petrol. Sci. Engng 175, 519–535.CrossRefGoogle Scholar
Niño, Y. & García, M. 1998 Experiments on saltation of sand in water. J. Hydraul. Engng 124 (10), 1014–1025.CrossRefGoogle Scholar
Oger, L., Ammi, M., Valance, A. & Beladjine, D. 2005 Discrete element method studies of the collision of one rapid sphere on 2D and 3D packings. Eur. Phys. J. E 17 (4), 467–76.CrossRefGoogle ScholarPubMed
Ouriemi, M., Aussillous, P. & Guazzelli, É. 2009 Sediment dynamics. Part 1. Bed-load transport by laminar shearing flows. J. Fluid Mech. 636, 295–319.CrossRefGoogle Scholar
Owen, P.R. 1964 Saltation of uniform grains in air. J. Fluid Mech. 20 (2), 225–242.CrossRefGoogle Scholar
Pähtz, T., Clark, A.H., Valyrakis, M. & Durán, O. 2020 The physics of sediment transport initiation, cessation, and entrainment across aeolian and fluvial environments. Rev. Geophys. 58 (1), e2019RG000679.CrossRefGoogle Scholar
Pähtz, T. & Durán, O. 2020 Unification of aeolian and fluvial sediment transport rate from granular physics. Phys. Rev. Lett. 124, 168001.CrossRefGoogle ScholarPubMed
Pähtz, T., Durán, O., Ho, T.-D., Valance, A. & Kok, J.F. 2015 The fluctuation energy balance in non-suspended fluid-mediated particle transport. Phys. Fluids 27, 013303.CrossRefGoogle Scholar
Pähtz, T., Kok, J.F. & Herrmann, H.J. 2012 The apparent roughness of a sand surface blown by wind from an analytical model of saltation. New J. Phys. 14, 043035.CrossRefGoogle Scholar
Ralaiarisoa, J.-L., Besnard, J.-B., Furieri, B., Dupont, P., Ould El Moctar, A., Naaim-Bouvet, F. & Valance, A. 2020 Transition from saltation to collisional regime in windblown sand. Phys. Rev. Lett. 124, 198501.CrossRefGoogle ScholarPubMed
van Rijn, L.C. 1984 Sediment transport. Part 1. Bed load transport. J. Hydraul. Engng 110 (10), 1431–1456.CrossRefGoogle Scholar
Sauermann, G., Kroy, K. & Herrmann, H.J. 2001 Continuum saltation model for sand dunes. Phys. Rev. E 64 (3), 031305.CrossRefGoogle ScholarPubMed
Seizilles, G., Lajeunesse, E., Devauchelle, O. & Bak, M. 2014 Cross-stream diffusion in bedload transport. Phys. Fluids 26 (1), 013302.CrossRefGoogle Scholar
Tsuji, Y., Kawaguchi, T. & Tanaka, T. 1993 Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 77 (1), 79–87.CrossRefGoogle Scholar
Valance, A., Rasmussen, K.R., Ould El Moctar, A. & Dupont, P. 2015 The physics of aeolian sand transport. C. R. Phys. 16 (1), 105–117.CrossRefGoogle Scholar