Article contents
Particle fountains in a confined environment
Published online by Cambridge University Press: 14 September 2018
Abstract
We present new experiments and theoretical models of the motion of relatively dense particles carried upwards by a liquid jet into a laterally confined space filled with the same liquid. The incoming jet is negatively buoyant and rises to a finite height, at which the dense mixture of liquid and particles, diluted by the entrainment of ambient liquid, falls back to the floor. The mixture further dilutes during the collapse and then spreads out across the floor and supplies an up-flow outside the fountain equal to the source volume flux plus the total entrained volume flux. The fate of the particles depends on the particle fall speed, 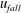 $u_{fall}$, compared to (i) the characteristic fountain velocity in the fountain core,
$u_{fall}$, compared to (i) the characteristic fountain velocity in the fountain core, 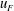 $u_{F}$, (ii) the maximum upward velocity in the ambient fluid outside the fountain,
$u_{F}$, (ii) the maximum upward velocity in the ambient fluid outside the fountain, 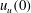 $u_{u}(0)$, which occurs at the base of the fountain, and (iii) the upward velocity in the ambient fluid above the top of the fountain associated with the original volume flux in the liquid jet,
$u_{u}(0)$, which occurs at the base of the fountain, and (iii) the upward velocity in the ambient fluid above the top of the fountain associated with the original volume flux in the liquid jet, 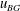 $u_{BG}$. From this comparison we identify four regimes. (I) If
$u_{BG}$. From this comparison we identify four regimes. (I) If 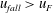 $u_{fall}>u_{F}$, then the particles separate from the fountain and settle on the floor. (II) If
$u_{fall}>u_{F}$, then the particles separate from the fountain and settle on the floor. (II) If 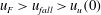 $u_{F}>u_{fall}>u_{u}(0)$, the particles are carried to the top of the fountain but then settle as the collapsing flow around the fountain spreads out across the floor; we do not observe particle suspension in the background flow. (III) For
$u_{F}>u_{fall}>u_{u}(0)$, the particles are carried to the top of the fountain but then settle as the collapsing flow around the fountain spreads out across the floor; we do not observe particle suspension in the background flow. (III) For 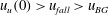 $u_{u}(0)>u_{fall}>u_{BG}$ we observe a particle-laden layer outside the fountain which extends from the floor of the tank to a point below the top of the fountain. The density of this lower particle-laden layer equals the density of the collapsing fountain fluid as it passes downwards through this interface. The collapsing fluid then spreads out horizontally through the depth of this particle-laden layer, instead of continuing downwards around the rising fountain. In the lower layer, the negatively buoyant source fluid in fact rises as a negatively buoyant jet, but this transitions into a fountain above the upper interface of the particle-laden layer. The presence of the particles in the lower layer reduces the density difference between fountain and environment, leading to an increase in the fountain height. (IV) If
$u_{u}(0)>u_{fall}>u_{BG}$ we observe a particle-laden layer outside the fountain which extends from the floor of the tank to a point below the top of the fountain. The density of this lower particle-laden layer equals the density of the collapsing fountain fluid as it passes downwards through this interface. The collapsing fluid then spreads out horizontally through the depth of this particle-laden layer, instead of continuing downwards around the rising fountain. In the lower layer, the negatively buoyant source fluid in fact rises as a negatively buoyant jet, but this transitions into a fountain above the upper interface of the particle-laden layer. The presence of the particles in the lower layer reduces the density difference between fountain and environment, leading to an increase in the fountain height. (IV) If 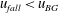 $u_{fall}<u_{BG}$ then an ascending front of particles rises above the fountain and eventually fills the entire tank up to the level where fluid is removed from the tank. We compare the results of a series of new laboratory experiments with simple theoretical investigations for each case, and discuss the relevance of our results.
$u_{fall}<u_{BG}$ then an ascending front of particles rises above the fountain and eventually fills the entire tank up to the level where fluid is removed from the tank. We compare the results of a series of new laboratory experiments with simple theoretical investigations for each case, and discuss the relevance of our results.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 4
- Cited by



