Article contents
Particle dynamics in the channel flow of a turbulent particle–gas suspension at high Stokes number. Part 2. Comparison of fluctuating force simulations and experiments
Published online by Cambridge University Press: 06 October 2011
Abstract
The particle and fluid velocity fluctuations in a turbulent gas–particle suspension are studied experimentally using two-dimensional particle image velocimetry with the objective of comparing the experiments with the predictions of fluctuating force simulations. Since the fluctuating force simulations employ force distributions which do not incorporate the modification of fluid turbulence due to the particles, it is of importance to quantify the turbulence modification in the experiments. For experiments carried out at a low volume fraction of 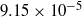 (mass loading is 0.19), where the viscous relaxation time is small compared with the time between collisions, it is found that the gas-phase turbulence is not significantly modified by the presence of particles. Owing to this, quantitative agreement is obtained between the results of experiments and fluctuating force simulations for the mean velocity and the root mean square of the fluctuating velocity, provided that the polydispersity in the particle size is incorporated in the simulations. This is because the polydispersity results in a variation in the terminal velocity of the particles which could induce collisions and generate fluctuations; this mechanism is absent if all of the particles are of equal size. It is found that there is some variation in the particle mean velocity very close to the wall depending on the wall-collision model used in the simulations, and agreement with experiments is obtained only when the tangential wall–particle coefficient of restitution is 0.7. The mean particle velocity is in quantitative agreement for locations more than 10 wall units from the wall of the channel. However, there are systematic differences between the simulations and theory for the particle concentrations, possibly due to inadequate control over the particle feeding at the entrance. The particle velocity distributions are compared both at the centre of the channel and near the wall, and the shape of the distribution function near the wall obtained in experiments is accurately predicted by the simulations. At the centre, there is some discrepancy between simulations and experiment for the distribution of the fluctuating velocity in the flow direction, where the simulations predict a bi-modal distribution whereas only a single maximum is observed in the experiments, although both distributions are skewed towards negative fluctuating velocities. At a much higher particle mass loading of 1.7, where the time between collisions is smaller than the viscous relaxation time, there is a significant increase in the turbulent velocity fluctuations by
(mass loading is 0.19), where the viscous relaxation time is small compared with the time between collisions, it is found that the gas-phase turbulence is not significantly modified by the presence of particles. Owing to this, quantitative agreement is obtained between the results of experiments and fluctuating force simulations for the mean velocity and the root mean square of the fluctuating velocity, provided that the polydispersity in the particle size is incorporated in the simulations. This is because the polydispersity results in a variation in the terminal velocity of the particles which could induce collisions and generate fluctuations; this mechanism is absent if all of the particles are of equal size. It is found that there is some variation in the particle mean velocity very close to the wall depending on the wall-collision model used in the simulations, and agreement with experiments is obtained only when the tangential wall–particle coefficient of restitution is 0.7. The mean particle velocity is in quantitative agreement for locations more than 10 wall units from the wall of the channel. However, there are systematic differences between the simulations and theory for the particle concentrations, possibly due to inadequate control over the particle feeding at the entrance. The particle velocity distributions are compared both at the centre of the channel and near the wall, and the shape of the distribution function near the wall obtained in experiments is accurately predicted by the simulations. At the centre, there is some discrepancy between simulations and experiment for the distribution of the fluctuating velocity in the flow direction, where the simulations predict a bi-modal distribution whereas only a single maximum is observed in the experiments, although both distributions are skewed towards negative fluctuating velocities. At a much higher particle mass loading of 1.7, where the time between collisions is smaller than the viscous relaxation time, there is a significant increase in the turbulent velocity fluctuations by 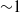 –2 orders of magnitude. Therefore, it becomes necessary to incorporate the modified fluid-phase intensity in the fluctuating force simulation; with this modification, the mean and mean-square fluctuating velocities are within 20–30 % of the experimental values.
–2 orders of magnitude. Therefore, it becomes necessary to incorporate the modified fluid-phase intensity in the fluctuating force simulation; with this modification, the mean and mean-square fluctuating velocities are within 20–30 % of the experimental values.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
Footnotes
Present address: CSIR Centre for Mathematical Modelling and Computer Simulation, Bangalore, India.
References
- 9
- Cited by


