Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T01:38:48.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle dispersion induced by vortical interactions in a particle-laden upward jet with a partial crossflow

Published online by Cambridge University Press:  09 March 2021

Jooyeon Park  and
Hyungmin Park Open the ORCID record for Hyungmin Park [Opens in a new window]
Jooyeon Park
Affiliation:
Department of Mechanical Engineering, Seoul National University, Seoul08826, Korea
Hyungmin Park*
Affiliation:
Department of Mechanical Engineering, Seoul National University, Seoul08826, Korea Institute of Advanced Machines and Design, Seoul National University, Seoul08826, Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

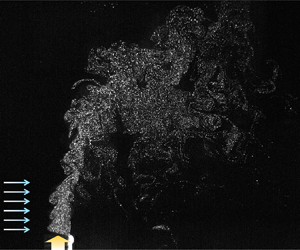
In the present study particle dispersions (concentrations) through vortical interactions are experimentally investigated for a particle-laden upward jet, with a horizontal crossflow covering a vertical range partially near the jet exit (Reynolds numbers of 1170–5200). We focus on the influences of the dynamics of counter-rotating vortex pairs existing in the flow on changes in the particle dispersion patterns, depending on the velocity (jet/crossflow) ratio and particle Stokes number ($St = 0.01\text {--}27.42$). Without crossflow, there is no dominant vortical structure along the horizontal direction; thus, the particles are not dispersed significantly out of the jet core in most cases, except for the case with the highest particle inertia (i.e. $St$). With crossflow, on the other hand, counter-rotating vortex pairs appear above the jet exit and become stronger as the velocity ratio decreases. With a lower velocity ratio, the vortices are tilted more toward the leeward side and dissipate faster. Driven by the vortex pairs, the drag force acting on the particles becomes stronger and, thus, particles with $St < 1.0$ are dragged out of the jet core following the rotation of the vortices. Those with $St \simeq 1.0$ are concentrated between the vortex pairs before the vortices collapse. When $St \gg 1.0$, particles are simply transported by the inertial effect. Finally, we suggest different regimes for particle dispersion (concentration) as classified by the Stokes number and velocity ratio, and elucidate their mechanisms, which are further extended to empirical particle dispersion models.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Multiphase and Particle-laden Flows: Multiphase flow Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A5
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abdelsamie, A.H. & Lee, C. 2012 Decaying versus stationary turbulence in particle-laden isotropic turbulence: turbulence modulation mechanism. Phys. Fluids 24, 015106.CrossRefGoogle Scholar
Acarlar, M.S. & Smith, C.R. 1987 A study of hairpin vortices in a laminar boundary layer. Part 2. Hairpin vortices generated by fluid injection. J. Fluid Mech. 175, 43–83.CrossRefGoogle Scholar
Anderson, S.L. & Longmire, E.K. 1995 Particle motion in the stagnation zone of an impinging air jet. J. Fluid Mech. 299, 333–366.CrossRefGoogle Scholar
Andreopoulos, J. 1982 Measurements in a jet-pipe flow issuing perpendicularly into a cross stream. Trans. ASME: J. Fluids Engng 104, 493–499.Google Scholar
Bagchi, P. & Balachandar, S. 2003 Inertial and viscous forces on a rigid sphere in straining flows at moderate Reynolds numbers. J. Fluid Mech. 481, 105–148.CrossRefGoogle Scholar
Bassenne, M., Moin, P. & Urzay, J. 2018 Wavelet multiresolution analysis of particle-laden turbulence. Phys. Rev. Fluids 3, 084304.CrossRefGoogle Scholar
Birzer, C.H., Kalt, P.A. & Nathan, G.J. 2012 The influences of particle mass loading on mean and instantaneous particle distributions in precessing jet flows. Intl J. Multiphase Flow 41, 13–22.CrossRefGoogle Scholar
Chauvat, G., Peplinski, A., Henningson, D.S. & Hanifi, A. 2020 Global linear analysis of a jet in cross-flow at low velocity ratios. J. Fluid Mech. 889, A12.CrossRefGoogle Scholar
Cheong, M., Birzer, C. & Lau, T. 2016 Laser attenuation correction for planar nephelometry concentration measurements. Exp. Techniques 40, 1075–1083.CrossRefGoogle Scholar
Choi, D. & Park, H. 2018 Flow around in-line sphere array at moderate Reynolds number. Phys. Fluids 30, 097104.CrossRefGoogle Scholar
Coimbra, C.F.M. & Rangel, R.H. 1998 General solution of the particle momentum equation in unsteady Stokes flows. J. Fluid Mech. 370, 53–72.CrossRefGoogle Scholar
Cortelezzi, L. & Karagozian, A.R. 2001 On the formation of the counter-rotating vortex pair in transverse jets. J. Fluid Mech. 446, 347–373.CrossRefGoogle Scholar
Dou, Z., Bragg, A.D., Hammond, A.L., Liang, Z., Collins, L.R. & Meng, H. 2018 Effects of Reynolds number and Stokes number on particle-pair relative velocity in isotropic turbulence: a systematic experimental study. J. Fluid Mech. 830, 271–292.CrossRefGoogle Scholar
Elghobashi, S. 2006 An updated classification map of particle-laden turbulent flows. In Proceedings of the IUTAM Symposium on Computational Multiphase Flow (ed. S. Balachandar & A. Prosperetti). Springer.Google Scholar
Fellouah, H., Ball, C. & Pollard, A. 2009 Reynolds number effects within the development region of a turbulent round free jet. Intl J. Heat Mass Transfer 52, 3943–3954.CrossRefGoogle Scholar
Ferreira, M.A. & Ganapathisubramani, B. 2020 PIV-based pressure estimation in the canopy of urban-like roughness. Exp. Fluids 61, 70.CrossRefGoogle Scholar
Fessler, J.R. & Eaton, J.K. 1997 Particle response in a planar sudden expansion flow. Exp. Therm. Fluid Sci. 15, 413–423.CrossRefGoogle Scholar
Fric, T.F. & Roshko, A. 1994 Vortical structure in the wake of a transverse jet. J. Fluid Mech. 279, 1–47.CrossRefGoogle Scholar
Fu, Y., Wang, T. & Gu, C.G. 2013 Experimental and numerical analyses of gas-solid-multiphase jet in cross-flow. Proc. Inst. Mech. Engrs 227, 61–79.CrossRefGoogle Scholar
Gibert, M., Xu, H. & Bodenschatz, E. 2012 Where do small, weakly inertial particles go in a turbulent flow? J. Fluid Mech. 698, 160–167.CrossRefGoogle Scholar
Goswami, P.S. & Kumaran, V. 2011 Particle dynamics in the channel flow of a turbulent particle-gas suspension at high Stokes number. Part 1. DNS and fluctuating force model. J. Fluid Mech. 687, 1–40.CrossRefGoogle Scholar
Guha, A. 2008 Transport and deposition of particles in turbulent and laminar flow. Annu. Rev. Fluid Mech. 40, 311–341.CrossRefGoogle Scholar
Hu, M., Peng, J.F., Sun, K., Yue, D.L., Guo, S., Wiedensohler, A. & Wu, Z.J. 2012 Estimation of size-resolved ambient particle density based on the measurement of aerosol number, mass, and chemical size distributions in the winter in Beijing. Environ. Sci. Technol. 46, 9941–9947.Google ScholarPubMed
Hwang, W. & Eaton, J.K. 2006 Homogeneous and isotropic turbulence modulation by small heavy ($St \sim 50$) particles. J. Fluid Mech. 564, 361–393.CrossRefGoogle Scholar
Kalt, P.A., Birzer, C.H. & Nathan, G.J. 2007 Corrections to facilitate planar imaging of particle concentration in particle-laden flows using Mie scattering. Part 1: collimated laser sheets. Appl. Opt. 46, 5823–5834.CrossRefGoogle ScholarPubMed
Kalt, P.A. & Nathan, G.J. 2007 Corrections to facilitate planar imaging of particle concentration in particle-laden flows using Mie scattering. Part 2: diverging laser sheets. Appl. Opt. 46, 7227–7236.CrossRefGoogle ScholarPubMed
Keffer, J.F. & Baines, W.D. 1963 The round turbulent jet in a cross-wind. J. Fluid Mech. 15, 481–496.CrossRefGoogle Scholar
Kelso, R.M., Lim, T.T. & Perry, A.E. 1996 An experimental study of round jets in cross-flow. J. Fluid Mech. 306, 111–144.CrossRefGoogle Scholar
Kim, M., Lee, J.H. & Park, H. 2016 Study of bubble-induced turbulence in upward laminar bubbly pipe flows measured with a two-phase particle image velocimetry. Exp. Fluids 57, 55.CrossRefGoogle Scholar
Kim, N., Kim, H. & Park, H. 2015 An experimental study on the effects of rough hydrophobic surfaces on the flow around a circular cylinder. Phys. Fluids 27, 085113.CrossRefGoogle Scholar
Kwon, S.J. & Seo, I.W. 2005 Reynolds number effects on the behavior of a non-buoyant round jet. Exp. Fluids 38, 801–812.CrossRefGoogle Scholar
Lau, T.C.W. & Nathan, G.J. 2014 Influence of Stokes number on the velocity and concentration distributions in particle-laden jets. J. Fluid Mech. 757, 432–457.CrossRefGoogle Scholar
Lau, T.C.W. & Nathan, G.J. 2016 The effect of Stokes number on particle velocity and concentration distributions in a well-characterised, turbulent, co-flowing two-phase jet. J. Fluid Mech. 809, 72–110.CrossRefGoogle Scholar
Lawson, N.J., Rudman, M., Guerra, A. & Liow, J.L. 1999 Experimental and numerical comparisons of the break-up of a large bubble. Exp. Fluids 26, 524–534.CrossRefGoogle Scholar
Lee, J. & Park, H. 2020 Bubble dynamics and bubble-induced agitation in the homogeneous bubble-swarm past a circular cylinder at small to moderate void fractions. Phys. Rev. Fluids 5, 054304.CrossRefGoogle Scholar
Li, W., Shao, L., Wang, Z., Shen, R., Yang, S. & Tang, U. 2010 Size, composition, and mixing state of individual aerosol particles in a South China coastal city. J. Environ. Sci. 22, 561–569.CrossRefGoogle Scholar
Liu, X., Jiang, Y., Zhang, N. & Li, J. 2016 Gas penetrating flow through dynamic particle clusters. Powder Technol. 297, 409–414.CrossRefGoogle Scholar
Liu, Y., Shen, L., Zamansky, R. & Coletti, F. 2020 Life and death of inertial particle clusters in turbulence. J. Fluid Mech. 902, R1.CrossRefGoogle Scholar
Longmire, E.K. & Eaton, J.K. 1992 Structure of a particle-laden round jet. J. Fluid Mech. 236, 217–257.CrossRefGoogle Scholar
Mahesh, K. 2013 The interaction of jets with crossflow. Annu. Rev. Fluid Mech. 45, 379–407.CrossRefGoogle Scholar
Marchioli, C. & Soldati, A. 2002 Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 468, 283–315.CrossRefGoogle Scholar
Maxey, M.R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow-fields. J. Fluid Mech. 174, 441–465.CrossRefGoogle Scholar
Maxey, M.R. & Riley, J.J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.CrossRefGoogle Scholar
Mi, J., Nobes, D.S. & Nathan, G.J. 2001 Influence of jet exit conditions on the passive scalar field of an axisymmetric free jet. J. Fluid Mech. 432, 91–125.CrossRefGoogle Scholar
Mi, J., Xu, M. & Zhou, T. 2013 Reynolds number influence on statistical behaviors of turbulence in a circular free jet. Phys. Fluids 25, 075101.CrossRefGoogle Scholar
Muppidi, S. & Mahesh, K. 2005 Study of trajectories of jets in crossflow using direct numerical simulations. J. Fluid Mech. 530, 81–100.CrossRefGoogle Scholar
Muppidi, S. & Mahesh, K. 2007 Direct numerical simulation of round turbulent jets in crossflow. J. Fluid Mech. 574, 59–84.CrossRefGoogle Scholar
Namer, I. & Ötügen, M.V. 1988 Velocity measurements in a plane turbulent air jet at moderate Reynolds numbers. Exp. Fluids 6, 387–399.CrossRefGoogle Scholar
Nathan, G.J., Mi, J., Alwahabi, Z.T., Newbold, G.J.R. & Nobes, D.S. 2006 Impacts of a jet's exit flow pattern on mixing and combustion performance. Prog. Energy Combust. Sci. 32, 496–538.CrossRefGoogle Scholar
Plesniak, M.W. & Cusano, D.M. 2005 Scalar mixing in a confined rectangular jet in crossflow. J. Fluid. Mech. 524, 1–45.CrossRefGoogle Scholar
Plesniak, M.W. & Yi, J. 2002 Dispersion of a particle-laden air jet in a confined rectangular crossflow. Powder Technol. 125, 168–178.Google Scholar
Poelma, C., Westerweel, J. & Ooms, G. 2007 Particle-fluid interactions in grid-generated turbulence. J. Fluid Mech. 589, 315–351.CrossRefGoogle Scholar
Pope, S.B. 2003 Turbulent Flows. Cambridge University Press.Google Scholar
Raffel, M., Willert, C.E. & Kompenhans, J. 2007 Particle Image Velocimetry: A Practical Guide. Springer.CrossRefGoogle Scholar
Reeks, M.W. 1983 The transport of discrete particles in inhomogeneous turbulence. J. Aerosol Sci. 14, 729–739.CrossRefGoogle Scholar
Rosenfeld, M., Kwak, D. & Vinokur, M. 1991 A fractional step solution method for the unsteady incompressible Navier–Stokes equations in generalized coordinate systems. J. Comput. Phys. 94, 102–137.CrossRefGoogle Scholar
Rubinow, S.I. & Keller, J.B. 1961 The transverse force on a spinning sphere moving in a viscous fluid. J. Fluid Mech. 11, 447–459.CrossRefGoogle Scholar
Saffman, P.G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22, 385–400.CrossRefGoogle Scholar
Sau, A., Sheu, T.W.H., Hwang, R.R. & Yang, W.C. 2004 Three-dimensional simulation of square jets in cross-flow. Phys. Rev. E 69, 066302.CrossRefGoogle ScholarPubMed
Sau, R. & Mahesh, K. 2008 Dynamics and mixing of vortex rings in crossflow. J. Fluid Mech. 604, 389–409.CrossRefGoogle Scholar
Schiller, L. & Neumann, A. 1933 Self-sustained oscillations in the wake of a sphere. Z. Verein. Deutsch. Ing. 77, 318–320.Google Scholar
Slater, S.A., Leeming, A.D. & Young, J.B. 2003 Particle deposition from two-dimensional turbulent gas flows. Intl J. Multiphase Flow 29, 721–750.CrossRefGoogle Scholar
Smith, S.H. & Mungal, M.G. 1998 Mixing, structure and scaling of the jet in crossflow. J. Fluid Mech. 357, 83–122.CrossRefGoogle Scholar
Squires, K.D. & Eaton, J.K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3, 1169–1178.CrossRefGoogle Scholar
Steinfeld, A. 2005 Solar thermochemical production of hydrogen – a review. Sol. Energy 78, 603–615.CrossRefGoogle Scholar
Su, L. & Mungal, M. 2004 Simultaneous measurements of scalar and velocity field evolution in turbulent crossflowing jets. J. Fluid Mech. 513, 1–45.CrossRefGoogle Scholar
Suresh, P.R., Srinivasan, K., Sundararajan, T. & Das, S.K. 2008 Reynolds number dependence of plane jet development in the transitional regime. Phys. Fluids 20, 044105.CrossRefGoogle Scholar
Tagawa, Y., Mercado, J.M., Prakash, V.N., Calzavarini, E., Sun, C. & Lohse, D. 2012 Three-dimensional Lagrangian Voronoï analysis for clustering of particles and bubbles in turbulence. J. Fluid Mech. 693, 201–215.CrossRefGoogle Scholar
Tang, L., Wen, F., Yang, Y., Crowe, C., Chung, J.N. & Troutt, T.R. 1992 Self-organizing particle dispersion mechanism in a plane wake. Phys. Fluids A 4, 2244–2251.CrossRefGoogle Scholar
Tong, C. & Warhaft, Z. 1994 Turbulence suppression in a jet by means of a fine ring. Phys. Fluids 6, 328–333.CrossRefGoogle Scholar
Tóth, B., Anthoine, J. & Riethmuller, M.L. 2009 Two-phase PIV method using two excitation and two emission spectra. Exp. Fluids 47, 475–487.CrossRefGoogle Scholar
Vuorinen, V. & Keskinen, K. 2016 DNSlab: a gateway to turbulent flow simulation in Matlab. Comput. Phys. Commun. 203, 278–289.CrossRefGoogle Scholar
Wang, G., Zheng, X. & Tao, J. 2017 a Very large scale motions and PM10 concentration in a high-Re boundary layer. Phys. Fluids 29, 061701.CrossRefGoogle Scholar
Wang, X., Zheng, X. & Wang, P. 2017 b Direct numerical simulation of particle-laden plane turbulent wall jet and the influence of Stokes number. Intl J. Multiphase Flow 92, 82–92.CrossRefGoogle Scholar
Wen, F., Kamalu, N., Chung, J.N., Crowe, C.T. & Troutt, T.R. 1992 Particle dispersion by vortex structures in plane mixing layers. Trans. ASME: J. Fluids Engng 114, 657–666.Google Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39, 1096–1100.CrossRefGoogle Scholar
Xu, M., Pollard, A., Mi, J., Secretain, F. & Sadeghi, H. 2013 Effects of Reynolds number on some properties of a turbulent jet from a long square pipe. Phys. Fluids 25, 035102.CrossRefGoogle Scholar
Yuan, L.L. & Street, R.L. 1998 Trajectory and entrainment of a round jet in crossflow. Phys. Fluids 10, 2323–2335.CrossRefGoogle Scholar
Zaichik, L.I. & Alipchenkov, V.M. 2005 Statistical models for predicting particle dispersion and preferential concentration in turbulent flows. Intl J. Heat Fluid Flow 26, 416–430.CrossRefGoogle Scholar
Zhang, J., Xu, M., Pollard, A. & Mi, J. 2013 Effects of external intermittency and mean shear on the spectral inertial-range exponent in a turbulent square jet. Phys. Rev. E 87, 053009.CrossRefGoogle Scholar