Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T16:52:13.820Z Has data issue: false hasContentIssue false
  • English
  • Français

A pancake droplet translating in a Hele-Shaw cell: lubrication film and flow field

Published online by Cambridge University Press:  15 June 2016

Lailai Zhu  and
François Gallaire
Lailai Zhu*
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, Ecole Polytechnique Fédérale de Lausanne, Lausanne, CH-1015, Switzerland
François Gallaire*
Affiliation:
Laboratory of Fluid Mechanics and Instabilities, Ecole Polytechnique Fédérale de Lausanne, Lausanne, CH-1015, Switzerland
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We adopt a boundary integral method to study the dynamics of a translating droplet confined in a Hele-Shaw cell in the Stokes regime. The droplet is driven by the motion of the ambient fluid with the same viscosity. We characterize the three-dimensional (3D) nature of the droplet interface and of the flow field. The interface develops an arc-shaped ridge near the rear-half rim with a protrusion in the rear and a laterally symmetric pair of higher peaks; this pair of protrusions has been identified by recent experiments (Huerre et al., Phys. Rev. Lett., vol. 115 (6), 2015, 064501) and predicted asymptotically (Burgess & Foster, Phys. Fluids A, vol. 2 (7), 1990, pp. 1105–1117). The mean film thickness is well predicted by the extended Bretherton model (Klaseboer et al., Phys. Fluids, vol. 26 (3), 2014, 032107) with fitting parameters. The flow in the streamwise wall-normal middle plane is featured with recirculating zones, which are partitioned by stagnation points closely resembling those of a two-dimensional droplet in a channel. Recirculation is absent in the wall-parallel, unconfined planes, in sharp contrast to the interior flow inside a moving droplet in free space. The preferred orientation of the recirculation results from the anisotropic confinement of the Hele-Shaw cell. 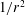On these planes, we identify a dipolar disturbance flow field induced by the travelling droplet and its $1/r^{2}$ spatial decay is confirmed numerically. We pinpoint counter-rotating streamwise vortex structures near the lateral interface of the droplet, further highlighting the complex 3D flow pattern.

JFM classification

Low-Reynolds-number flows: Boundary integral methods Drops and Bubbles: Drops Low-Reynolds-number flows: Hele-Shaw flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 955 - 969
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aussillous, P. & Quéré, D. 2000 Quick deposition of a fluid on the wall of a tube. Phys. Fluids 12 (10), 2367–2371.Google Scholar
Baroud, C. N., Gallaire, F. & Dangla, R. 2010 Dynamics of microfluidic droplets. Lab Chip 10 (16), 2032–2045.Google Scholar
Beatus, T., Tlusty, T. & Bar-Ziv, R. 2006 Phonons in a one-dimensional microfluidic crystal. Nat. Phys. 2 (11), 743–748.Google Scholar
Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10 (02), 166–188.Google Scholar
Burgess, D. & Foster, M. R. 1990 Analysis of the boundary conditions for a Hele-Shaw bubble. Phys. Fluids 2 (7), 1105–1117.Google Scholar
Cantat, I. 2013 Liquid meniscus friction on a wet plate: bubbles, lamellae, and foamsa. Phys. Fluids 25 (3), 031303.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 Nek5000: https://nek5000.mcs.anl.gov/.Google Scholar
Gallaire, F., Meliga, P., Laure, P. & Baroud, C. N. 2014 Marangoni induced force on a drop in a Hele Shaw cell. Phys. Fluids 26 (6), 062105.Google Scholar
Hernández-Ortiz, J. P., de Pablo, J. J. & Graham, M. D. 2007 Fast computation of many-particle hydrodynamic and electrostatic interactions in a confined geometry. Phys. Rev. Lett. 98 (14), 140602.Google Scholar
Hodges, S. R., Jensen, O. E. & Rallison, J. M. 2004 The motion of a viscous drop through a cylindrical tube. J. Fluid Mech. 501, 279–301.Google Scholar
Huerre, A., Theodoly, O., Leshansky, A. M., Valignat, M. P., Cantat, I. & Jullien, M. C. 2015 Droplets in microchannels: dynamical properties of the lubrication film. Phys. Rev. Lett. 115 (6), 064501.Google Scholar
Klaseboer, E., Gupta, R. & Manica, R. 2014 An extended Bretherton model for long Taylor bubbles at moderate capillary numbers. Phys. Fluids 26 (3), 032107.Google Scholar
Kumar, A. & Graham, M. D. 2012 Accelerated boundary integral method for multiphase flow in non-periodic geometries. J. Comput. Phys. 231, 6682–6713.Google Scholar
Lac, E. & Sherwood, J. D. 2009 Motion of a drop along the centreline of a capillary in a pressure-driven flow. J. Fluid Mech. 640, 27–54.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Lhuissier, H., Tagawa, Y., Tran, T. & Sun, C. 2013 Levitation of a drop over a moving surface. J. Fluid Mech. 733, R4.Google Scholar
Ling, Y., Fullana, J. M., Popinet, S. & Josserand, C. 2016 Droplet migration in a Hele-Shaw cell: effect of the lubrication film on the droplet dynamics. Phys. Fluids 28 (6), 062001.Google Scholar
Martinez, M. J. & Udell, K. S. 1990 Axisymmetric creeping motion of drops through circular tubes. J. Fluid Mech. 210, 565–591.Google Scholar
Maxworthy, T. 1986 Bubble formation, motion and interaction in a Hele-Shaw cell. J. Fluid Mech. 173, 95–114.Google Scholar
Meiburg, E. 1989 Bubbles in a Hele-Shaw cell: numerical simulation of three-dimensional effects. Phys. Fluids 1 (6), 938–946.Google Scholar
Nagel, M. & Gallaire, F. 2015 Boundary elements method for microfluidic two-phase flows in shallow channels. Comput. Fluids 107, 272–284.Google Scholar
Park, C.-W. & Homsy, G. M. 1984 Two-phase displacement in Hele Shaw cells: theory. J. Fluid Mech. 139, 291–308.CrossRefGoogle Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228 (16), 5838–5866.Google Scholar
Pranay, P., Anekal, S. G., Hernandez-Ortiz, J. P. & Graham, M. D. 2010 Pair collisions of fluid-filled elastic capsules in shear flow: effects of membrane properties and polymer additives. Phys. Fluids 22, 123103.Google Scholar
Saito, M., Tagawa, Y. & Lhuissier, H.2014 APS gallery of fluid motion (v0056): steady drop levitation. http://dx.doi.org/10.1103/APS.DFD.2014.GFM.V0056#sthash.vpdMpRtS.dpuf.Google Scholar
Shen, B., Leman, M., Reyssat, M. & Tabeling, P. 2014 Dynamics of a small number of droplets in microfluidic Hele-Shaw cells. Exp. Fluids 55 (5), 1–10.Google Scholar
Stokes, G. G. 1898 Mathematical proof of the identity of the stream lines obtained by means of a viscous film with those of a perfect fluid moving in two dimensions. In Report of the Sixty-Eighth Meeting of the British Association for the Advancement of Science, pp. 143–144.Google Scholar
Tanveer, S. 1986 The effect of surface tension on the shape of a Hele-Shaw cell bubble. Phys. Fluids 29 (11), 3537–3548.Google Scholar
Taylor, G. I. 1961 Deposition of a viscous fluid on the wall of a tube. J. Fluid Mech. 10 (02), 161–165.Google Scholar
Taylor, G. I. & Saffman, P. G. 1959 A note on the motion of bubbles in a Hele-Shaw cell and porous medium. Q. J. Mech. Appl. Maths 12 (3), 265–279.Google Scholar
Teh, S.-Y., Lin, R., Hung, L.-H. & Lee, A. P. 2008 Droplet microfluidics. Lab Chip 8 (2), 198–220.Google Scholar
Teletzke, G. F., Davis, H. T. & Scriven, L. E. 1988 Wetting hydrodynamics. Rev. Phys. Appl. 23 (6), 989–1007.Google Scholar
Westborg, H. & Hassager, O. 1989 Creeping motion of long bubbles and drops in capillary tubes. J. Colloid Interface Sci. 133 (1), 135–147.Google Scholar
Zhu, L. & Brandt, L. 2015 The motion of a deforming capsule through a corner. J. Fluid Mech. 770, 374–397.Google Scholar
Zhu, L., Lauga, E. & Brandt, L. 2013 Low-Reynolds number swimming in a capillary tube. J. Fluid Mech. 726, 285–311.Google Scholar
Zhu, L., Rorai, C., Dhrubaditya, M. & Brandt, L. 2014 A microfluidic device to sort capsules by deformability: a numerical study. Soft Matt. 10, 7705–7711.Google Scholar
Zinchenko, A. Z. & Davis, R. H. 2006 A boundary-integral study of a drop squeezing through interparticle constrictions. J. Fluid Mech. 564, 227–266.Google Scholar
Zinchenko, A. Z. & Davis, R. H. 2013 Emulsion flow through a packed bed with multiple drop breakup. J. Fluid Mech. 725, 611–663.Google Scholar