Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wei, Tie
Li, Zhaorui
and
Wang, Yanxing
2023.
New formulations for the mean wall-normal velocity and Reynolds shear stress in a turbulent boundary layer under zero pressure gradient.
Journal of Fluid Mechanics,
Vol. 969,
Issue. ,
Deshpande, Rahul
van den Bogaard, Aron
Vinuesa, Ricardo
Lindić, Luka
and
Marusic, Ivan
2023.
Reynolds-number effects on the outer region of adverse-pressure-gradient turbulent boundary layers.
Physical Review Fluids,
Vol. 8,
Issue. 12,
Wei, Tie
Li, Zhaorui
Knopp, Tobias
and
Vinuesa, Ricardo
2023.
The mean wall-normal velocity in turbulent boundary layer flows under pressure gradient.
Journal of Fluid Mechanics,
Vol. 975,
Issue. ,
Anbarlooei, Hamidreza
Ramos, Fabio
and
Cruz, Daniel O. A.
2023.
Asymptotic scaling laws for the skin friction of zero pressure gradient boundary layers.
Physical Review Fluids,
Vol. 8,
Issue. 8,
Silva, Leandro J.O.
and
Wolf, William R.
2024.
Embedded shear layers in turbulent boundary layers of a NACA0012 airfoil at high angles of attack.
International Journal of Heat and Fluid Flow,
Vol. 107,
Issue. ,
p.
109353.
Yang, Xiang I.A.
Chen, Peng E.S.
Zhang, Wen
and
Kunz, Robert
2024.
Predictive near-wall modelling for turbulent boundary layers with arbitrary pressure gradients.
Journal of Fluid Mechanics,
Vol. 993,
Issue. ,
Bi, Wei-Tao
Du, Tan-Tan
Chen, Jun
and
She, Zhen-Su
2024.
Mean-flow structures of the turbulent boundary layers bounding a two-dimensional separation bubble.
Physics of Fluids,
Vol. 36,
Issue. 8,
Han, Mingze
Ma, Mingze
and
Yan, Chao
2024.
Consistent outer scaling and analysis of adverse pressure gradient turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 982,
Issue. ,
Ma, Mingze
Bai, Ruijie
Song, Hanqi
Zhang, Jinrong
and
Yan, Chao
2024.
Asymptotic expansions and scaling of turbulent boundary layers in adverse pressure gradients.
Physics of Fluids,
Vol. 36,
Issue. 6,
Medzorian, Jack R.
and
Lynch, Stephen P.
2024.
Effect of Freestream Turbulence on Adverse Pressure Gradient Turbulent Boundary Layers.
Dong, Siwei
Yu, Ming
Tong, Fulin
Wang, Qian
and
Yuan, Xianxu
2024.
Hypersonic turbulent boundary layer over the windward side of a lifting body.
Journal of Fluid Mechanics,
Vol. 988,
Issue. ,
Gungor, Taygun R.
Gungor, Ayse G.
and
Maciel, Yvan
2024.
Turbulent boundary layer response to uniform changes of the pressure force contribution.
Journal of Fluid Mechanics,
Vol. 997,
Issue. ,
Joseph, Klewicki
Richard, Sandberg
Tobias, Knopp
William, Devenport
Daniel, Fritsch
Vidya, Vishwanathan
Ralph, Volino
Serge, Toxopeus
Beverley, McKeon
and
Luis, Eca
2024.
On the physical structure, modelling and computation-based prediction of two-dimensional, smooth-wall turbulent boundary layers subjected to streamwise pressure gradients.
Journal of Turbulence,
Gomez, Salvador R.
and
McKeon, Beverley J.
2025.
Linear analysis characterizes pressure gradient history effects in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 1002,
Issue. ,
Wei, Tie
Knopp, Tobias
and
Li, Zhaorui
2025.
Energy thickness in turbulent boundary layer flows.
Journal of Fluid Mechanics,
Vol. 1003,
Issue. ,
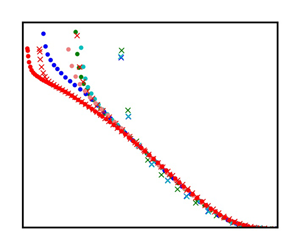
 $y_{m}$, is employed to determine the proper scales for the outer region of an APG TBL. An outer length scale is proposed as
$y_{m}$, is employed to determine the proper scales for the outer region of an APG TBL. An outer length scale is proposed as  $\delta _e - y_{m}$, where
$\delta _e - y_{m}$, where  $\delta _e$ is the boundary layer thickness. An outer velocity scale for the mean streamwise velocity deficit is proposed as
$\delta _e$ is the boundary layer thickness. An outer velocity scale for the mean streamwise velocity deficit is proposed as  $U_e - U_{m}$, where
$U_e - U_{m}$, where  $U_e$ and
$U_e$ and  $U_m$ are the mean streamwise velocities at the boundary layer edge and
$U_m$ are the mean streamwise velocities at the boundary layer edge and  $y_{m}$, respectively. An outer velocity scale for the mean wall-normal velocity deficit is proposed as
$y_{m}$, respectively. An outer velocity scale for the mean wall-normal velocity deficit is proposed as  $V_e - V_{m}$, where
$V_e - V_{m}$, where  $V_e$ and
$V_e$ and  $V_{m}$ are the wall-normal velocities at
$V_{m}$ are the wall-normal velocities at  $\delta _e$ and
$\delta _e$ and  $y_{m}$, respectively. The maximum Reynolds shear stress is found to scale as
$y_{m}$, respectively. The maximum Reynolds shear stress is found to scale as  $(\delta _e - y_{m}) U_e \,{\rm d}U_e/{{\rm d}x}$. The new outer scaling collapses well the experimental and numerical data on APG TBLs over a wide range of Reynolds numbers and strengths of pressure gradient. Approximations of the new scaling are developed for TBLs under strong APG and at high Reynolds numbers. The relationships between the new scales and previously proposed scales are discussed.
$(\delta _e - y_{m}) U_e \,{\rm d}U_e/{{\rm d}x}$. The new outer scaling collapses well the experimental and numerical data on APG TBLs over a wide range of Reynolds numbers and strengths of pressure gradient. Approximations of the new scaling are developed for TBLs under strong APG and at high Reynolds numbers. The relationships between the new scales and previously proposed scales are discussed.