Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T14:39:14.011Z Has data issue: false hasContentIssue false
  • English
  • Français

Outer scales and parameters of adverse-pressure-gradient turbulent boundary layers

Published online by Cambridge University Press:  03 April 2018

Yvan Maciel Open the ORCID record for Yvan Maciel [Opens in a new window] ,
Tie Wei Open the ORCID record for Tie Wei [Opens in a new window] ,
Ayse G. Gungor  and
Mark P. Simens
Yvan Maciel*
Affiliation:
Department of Mechanical Engineering, Laval University, Quebec City, QC, G1V 0A6Canada
Tie Wei
Affiliation:
Department of Mechanical Engineering, New Mexico Institute of Mining and Technology, Socorro, NM 87801, USA
Ayse G. Gungor
Affiliation:
Faculty of Aeronautics and Astronautics, Istanbul Technical University, 34469 Maslak, Istanbul, Turkey
Mark P. Simens
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, 28040 Madrid, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A clear and consistent framework for the analysis of the outer region of adverse-pressure-gradient turbulent boundary layers is established in this paper based on basic principles and theory, and the help of six adverse-pressure-gradient turbulent boundary layer databases and a zero-pressure-gradient one. Outer velocity and length scales for the mean velocity defect and the Reynolds stresses are discussed first. The conditions of validity of four velocity scales are determined in terms of the shape factor, since one scale is restricted to small velocity-defect boundary layers (the friction velocity 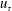$u_{\unicode[STIX]{x1D70F}}$), one to large-defect ones (the pressure-gradient velocity 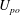$U_{po}$), while the two others are proper scales for all velocity-defect conditions (the Zagarola–Smits velocity 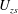$U_{zs}$ and the mixing-layer-type velocity 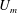$U_{m}$). The turbulent boundary layer equations are then used to bring out, in a consistent manner and without assuming any self-similar behaviour, a set of non-dimensional parameters characterizing the outer region of turbulent boundary layers with arbitrary pressure gradients. In terms of a generic outer length scale 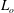$L_{o}$ and velocity scale 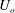$U_{o}$, these non-dimensional parameters are the pressure-gradient parameter 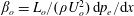$\unicode[STIX]{x1D6FD}_{o}=L_{o}/(\unicode[STIX]{x1D70C}U_{o}^{2})\,\text{d}p_{e}/\text{d}x$, the Reynolds number 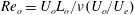$Re_{o}=U_{o}L_{o}/\unicode[STIX]{x1D708}(U_{o}/U_{e})$ and the inertial parameter 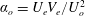$\unicode[STIX]{x1D6FC}_{o}=U_{e}V_{e}/U_{o}^{2}$, where 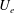$U_{e}$ and 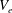$V_{e}$ are respectively the streamwise and wall-normal components of mean velocity at the boundary layer edge. These parameters have a clear physical meaning: they are ratios of the order of magnitude of forces, with the Reynolds shear stress gradient (apparent turbulent force) as the reference force – inertial to apparent turbulent forces for 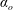$\unicode[STIX]{x1D6FC}_{o}$, pressure to apparent turbulent forces for 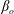$\unicode[STIX]{x1D6FD}_{o}$ and apparent turbulent to viscous forces for 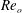$Re_{o}$. We discuss at length their significance and determine under what conditions they retain their meaning depending on the outer velocity scale that is considered. The seven boundary layer databases are analysed and compared using the established framework. An astonishing and impressive result is obtained: by choosing 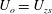$U_{o}=U_{zs}$, the streamwise evolution of the three ratios of forces in the outer region can be accurately followed with 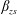$\unicode[STIX]{x1D6FD}_{zs}$, 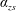$\unicode[STIX]{x1D6FC}_{zs}$ and 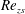$Re_{zs}$ in all these flows – not just the order of magnitude of these ratios. This cannot be achieved with 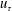$u_{\unicode[STIX]{x1D70F}}$ and 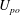$U_{po}$, and only imperfectly with 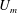$U_{m}$. Consequently, 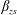$\unicode[STIX]{x1D6FD}_{zs}$, 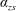$\unicode[STIX]{x1D6FC}_{zs}$ and 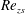$Re_{zs}$ can be used to follow – in a global sense – the streamwise evolution of the streamwise mean momentum balance in the outer region.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 844 , 10 June 2018 , pp. 5 - 35
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H. 2017 Reynolds-number dependence of wall-pressure fluctuations in a pressure-induced turbulent separation bubble. J. Fluid Mech. 833, 563–598.10.1017/jfm.2017.694Google Scholar
Afzal, N. 1983 Analysis of a turbulent boundary layer subjected to a strong adverse pressure gradient. Intl J. Engng Sci. 21 (6), 563–576.10.1016/0020-7225(83)90104-0Google Scholar
Afzal, N. 2008 Turbulent boundary layer with negligible wall stress. Trans. ASME J. Fluids Engng 130 (5), 051205.10.1115/1.2903754Google Scholar
Angele, K. P. & Muhammad-Klingmann, B. 2006 PIV measurements in a weakly separating and reattaching turbulent boundary layer. Eur. J. Mech. (B/Fluids) 25 (2), 204–222.10.1016/j.euromechflu.2005.05.003Google Scholar
Bobke, A., Vinuesa, R., Örlü, R. & Schlatter, P. 2017 History effects and near equilibrium in adverse-pressure-gradient turbulent boundary layers. J. Fluid Mech. 820, 667–692.10.1017/jfm.2017.236Google Scholar
Clauser, F. H. 1954 The turbulent boundary layer in adverse pressure gradient. J. Aero. Sci. 21, 91–108.10.2514/8.2938Google Scholar
Clauser, F. H. 1956 The turbulent boundary layer. In Advances in Applied Mechanics (ed. Dryden, H. L. & von Karman, Th.), vol. 4, pp. 1–51. Elsevier.Google Scholar
Coles, D. E. 1956 The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1 (02), 191–226.10.1017/S0022112056000135Google Scholar
Coles, D. E. 1969 The young persons guide to the data. In 1968 AFOSR-IFP-Stanford Conference Computation of Turbulent Boundary Layers: Compiled Data, vol. 2, pp. 1–45. Thermosciences Division, Stanford University.Google Scholar
Coles, D. E. & Hirst, E.(Eds) 1969 1968 AFOSR-IFP-Stanford Conference Computation of Turbulent Boundary Layers: Compiled Data, vol. 2. Thermosciences Division, Stanford University.Google Scholar
Cuvier, C., Srinath, S., Stanislas, M., Foucaut, J. M., Laval, J. P., Khler, C. J., Hain, R., Scharnowski, S., Schrder, A., Geisler, R. et al. 2017 Extensive characterisation of a high Reynolds number decelerating boundary layer using advanced optical metrology. J. Turbul. 18 (10), 929–972.10.1080/14685248.2017.1342827Google Scholar
Durbin, P. A. & Belcher, S. E. 1992 Scaling of adverse-pressure-gradient turbulent boundary layers. J. Fluid Mech. 238, 699–722.10.1017/S0022112092001873Google Scholar
Elsberry, K., Loeffler, J., Zhou, M. D. & Wygnanski, I. 2000 An experimental study of a boundary layer that is maintained on the verge of separation. J. Fluid Mech. 423, 227–261.10.1017/S0022112000001828Google Scholar
Gungor, A. G., Maciel, Y., Simens, M. P. & Gungor, T. 2017 Direct numerical simulation of a non-equilibrium adverse pressure gradient boundary layer up to Re 𝜃 = 8000. In 16th European Turbulence Conference, Stockholm, Sweden, European Mechanics Society.Google Scholar
Gungor, A. G., Maciel, Y., Simens, M. P. & Soria, J. 2014 Analysis of a turbulent boundary layer subjected to a strong adverse pressure gradient. J. Phys.: Conf. Ser. 506, 012007.Google Scholar
Gungor, A. G., Maciel, Y., Simens, M. P. & Soria, J. 2016 Scaling and statistics of large-defect adverse pressure gradient turbulent boundary layers. Intl J. Heat Fluid Flow 59, 109–124.10.1016/j.ijheatfluidflow.2016.03.004Google Scholar
Harun, Z., Monty, J. P., Mathis, R. & Marusic, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J. Fluid Mech. 715, 477–498.10.1017/jfm.2012.531Google Scholar
Hickel, S. & Adams, N. A. 2008 Implicit LES applied to zero-pressure-gradient and adverse-pressure-gradient boundary-layer turbulence. Intl J. Heat Fluid Flow 29 (3), 626–639.10.1016/j.ijheatfluidflow.2008.03.008Google Scholar
Hosseini, S. M., Vinuesa, R., Schlatter, P., Hanifi, A. & Henningson, D. S. 2016 Direct numerical simulation of the flow around a wing section at moderate Reynolds number. Intl J. Heat Fluid Flow 61, 117–128.10.1016/j.ijheatfluidflow.2016.02.001Google Scholar
Indinger, T., Buschmann, M. T. & Gad-el Hak, M. 2006 Mean-velocity profile of turbulent boundary layers approaching separation. AIAA J. 44, 2465–2474.10.2514/1.18905Google Scholar
Inoue, M., Pullin, D. I., Harun, Z. & Marusic, I. 2013 LES of the adverse-pressure gradient turbulent boundary layer. Intl J. Heat Fluid Flow 44, 293–300.10.1016/j.ijheatfluidflow.2013.06.011Google Scholar
Kader, B. A. & Yaglom, A. M. 1978 Similarity treatment of moving-equilibrium turbulent boundary layers in adverse pressure gradients. J. Fluid Mech. 89 (02), 305–342.10.1017/S0022112078002621Google Scholar
Kitsios, V., Sekimoto, A., Atkinson, C., Sillero, J. A., Borrell, G., Gungor, A. G., Jimnez, J. & Soria, J. 2017 Direct numerical simulation of a self-similar adverse pressure gradient turbulent boundary layer at the verge of separation. J. Fluid Mech. 829, 392–419.10.1017/jfm.2017.549Google Scholar
Kline, S. J., Coles, D. E. & Hirst, E.(Eds) 1969 1968 AFOSR-IFP-Stanford Conference Computation of Turbulent Boundary Layers: Methods, Predictions, Evaluation, and Flow Structure, vol. 1. Thermosciences Division, Stanford University.Google Scholar
Knopp, T., Buchmann, N. A., Schanz, D., Eisfeld, B., Cierpka, C., Hain, R., Schrder, A. & Khler, C. J. 2015 Investigation of scaling laws in a turbulent boundary layer flow with adverse pressure gradient using PIV. J. Turbul. 16 (3), 250–272.10.1080/14685248.2014.943906Google Scholar
Knopp, T., Reuther, N., Novara, M., Schulein, E., Schanz, D., Schrder, A. & Khler, C. J. 2017 Investigation of a turbulent boundary layer flow at high Reynolds number using particle-imaging and implications for RANS modeling. In Tenth International Symposium on Turbulence and Shear Flow Phenomena (TSFP10), Chicago, USA, Darmstadt University of Technology.Google Scholar
Lee, J. H. & Sung, H. J. 2009 Structures in turbulent boundary layers subjected to adverse pressure gradients. J. Fluid Mech. 639, 101–131.10.1017/S0022112009990814Google Scholar
Logdberg, O., Angele, K. & Alfredsson, P. H. 2008 On the scaling of turbulent separating boundary layers. Phys. Fluids 20, 075104.10.1063/1.2958317Google Scholar
Ludwieg, H. & Tillmann, W.1949 Untersuchungen über die wandschubspannung in turbulenten reibungsschichten. Ing.-Arch.; translated as Investigations of the wall-shearing stress in turbulent boundary layers, NACA Tech. Mem. No. 1285, 1950, 17.Google Scholar
Maciel, Y., Gungor, A. G. & Simens, M. 2017 Structural differences between small and large momentum-defect turbulent boundary layers. Intl J. Heat Fluid Flow 67, 95–110.10.1016/j.ijheatfluidflow.2017.07.011Google Scholar
Maciel, Y., Rossignol, K. S. & Lemay, J. 2006a A study of a turbulent boundary layer in stalled-airfoil-type flow conditions. Exp. Fluids 41 (4), 573–590.10.1007/s00348-006-0182-1Google Scholar
Maciel, Y., Rossignol, K. S. & Lemay, J. 2006b Self-similarity in the outer region of adverse-pressure-gradient turbulent boundary layers. AIAA J. 44 (11), 2450–2464.10.2514/1.19234Google Scholar
Marquillie, M., Laval, J.-P. & Dolganov, R. 2008 Direct numerical simulation of a separated channel flow with a smooth profile. J. Turbul. 9 (1).10.1080/14685240701767332Google Scholar
McDonald, H. 1969 The effect of pressure gradient on the law of the wall in turbulent flow. J. Fluid Mech. 35 (02), 311–336.10.1017/S0022112069001133Google Scholar
Mellor, G. L. & Gibson, D. M. 1966 Equilibrium turbulent boundary layers. J. Fluid Mech. 24 (02), 225–253.10.1017/S0022112066000612Google Scholar
Melnik, R. E. 1989 An asymptotic theory of turbulent separation. Comput. Fluids 17 (1), 165–184.10.1016/0045-7930(89)90014-5Google Scholar
Na, Y. & Moin, P. 1998 Direct numerical simulation of separated turbulent boundary layer. J. Fluid Mech. 374, 379–405.10.1017/S002211209800189XGoogle Scholar
Panton, R. L. 2005 Review of wall turbulence as described by composite expansions. Appl. Mech. Rev. 58 (1), 1–36.10.1115/1.1840903Google Scholar
Perry, A. E., Bell, J. B. & Joubert, P. N. 1966 Velocity and temperature profiles in adverse pressure gradient turbulent boundary layers. J. Fluid Mech. 25 (02), 299–320.10.1017/S0022112066001666Google Scholar
Perry, A. E. & Schofield, W. H. 1973 Mean velocity and shear stress distributions in turbulent boundary layers. Phys. Fluids 16 (12), 2068–2074.10.1063/1.1694267Google Scholar
Rahgozar, S. & Maciel, Y. 2012 Statistical analysis of low- and high-speed large-scale structures in the outer region of an adverse pressure gradient turbulent boundary layer. J. Turbul. 13, 1–24.10.1080/14685248.2012.726995Google Scholar
Rotta, J.1950 Uber die theorie der turbulenten grenzschichten. Mitt. Max Planck Inst. Strmungsforsch., Göttingen; translated as On the theory of turbulent boundary layers, NACA Tech. Mem. No. 1344, 1953, 1.Google Scholar
Sato, M., Asada, K., Nonomura, T., Kawai, S. & Fujii, K. 2017 Large-eddy simulation of NACA 0015 airfoil flow at Reynolds number of 1. 6 × 106 . AIAA J. 55 (2), 673–679.10.2514/1.J054963Google Scholar
Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory, 8th edn. Springer.10.1007/978-3-642-85829-1Google Scholar
Sillero, J., Jiménez, J. & Moser, R. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 25, 105102.10.1063/1.4823831Google Scholar
Skåre, P. E. & Krogstad, P. Å. 1994 A turbulent equilibrium boundary layer near separation. J. Fluid Mech. 272, 319–348.Google Scholar
Skote, M. & Henningson, D. S. 2002 Direct numerical simulation of separated turbulent boundary layer. J. Fluid Mech. 471, 107–136.10.1017/S0022112002002173Google Scholar
Spalart, P. R. & Watmuff, J. H. 1993 Experimental and numerical study of a turbulent boundary layer with pressure gradients. J. Fluid Mech. 249, 337–371.10.1017/S002211209300120XGoogle Scholar
Townsend, A. A. 1956a The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Townsend, A. A. 1956b The properties of equilibrium boundary layers. J. Fluid Mech. 1 (06), 561–573.10.1017/S0022112056000378Google Scholar
Townsend, A. A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11 (01), 97–120.10.1017/S0022112061000883Google Scholar
Vinuesa, R., Bobke, A., Örlü, R. & Schlatter, P. 2016 On determining characteristic length scales in pressure-gradient turbulent boundary layers. Phys. Fluids 28 (5), 055101.10.1063/1.4947532Google Scholar
Yajnik, K. S. 1970 Asymptotic theory of turbulent shear flows. J. Fluid Mech. 42 (2), 411–427 10.1017/S0022112070001350Google Scholar