Article contents
Oscillatory Marangoni flows with inertia
Published online by Cambridge University Press: 19 August 2016
Abstract
When the surface of a liquid has a non-uniform distribution of a surfactant that lowers surface tension, the resulting variation in surface tension drives a flow that spreads the surfactant towards a uniform distribution. We study the spreading dynamics of an insoluble and non-diffusing surfactant on an initially motionless liquid. We derive solutions for the evolution over time of sinusoidal variations in surfactant concentration with a small initial amplitude relative to the average concentration. In this limit, the coupled flow and surfactant transport equations are linear. In contrast to exponential decay when the inertia of the flow is negligible, the solution for unsteady Stokes flow exhibits oscillations when inertia is sufficient to spread the surfactant beyond a uniform distribution. This oscillatory behaviour exhibits two properties that distinguish it from that of a simple harmonic oscillator: the amplitude changes sign at most three times, and the decay at late times follows a power law with an exponent of 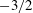 $-3/2$. As the surface oscillates, the structure of the subsurface flow alternates between one and two rows of counter-rotating vortices, starting with one row and ending with two during the late-time monotonic decay. We also examine numerically the evolution of the surfactant distribution when the system is nonlinear due to a large initial amplitude.
$-3/2$. As the surface oscillates, the structure of the subsurface flow alternates between one and two rows of counter-rotating vortices, starting with one row and ending with two during the late-time monotonic decay. We also examine numerically the evolution of the surfactant distribution when the system is nonlinear due to a large initial amplitude.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 7
- Cited by



