Article contents
Oscillatory and streaming flow between two spheres due to combined oscillations
Published online by Cambridge University Press: 03 August 2017
Abstract
The flow induced by the combined torsional and transverse oscillations of a sphere with amplitude ratio  $\unicode[STIX]{x1D6FC}$ and phase difference
$\unicode[STIX]{x1D6FC}$ and phase difference 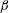 $\unicode[STIX]{x1D6FD}$ in a concentric spherical container is examined. Analytical solutions of the leading-order flow field and shear stress profiles have been obtained. Steady streaming flows are also analysed not only for the case of unrestricted Womersley number
$\unicode[STIX]{x1D6FD}$ in a concentric spherical container is examined. Analytical solutions of the leading-order flow field and shear stress profiles have been obtained. Steady streaming flows are also analysed not only for the case of unrestricted Womersley number 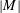 $|M|$, but also in the low-frequency
$|M|$, but also in the low-frequency 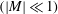 $(|M|\ll 1)$ and high-frequency (
$(|M|\ll 1)$ and high-frequency (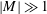 $|M|\gg 1$) limits. At high frequency, the flow field has been divided into three regions: two boundary layers and the outer region. The streaming flow field is determined for the limiting case of the streaming Reynolds number
$|M|\gg 1$) limits. At high frequency, the flow field has been divided into three regions: two boundary layers and the outer region. The streaming flow field is determined for the limiting case of the streaming Reynolds number 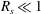 $R_{s}\ll 1$. The results are compared with those of single torsional or transverse oscillation, and found to match very well. The amplitude ratio
$R_{s}\ll 1$. The results are compared with those of single torsional or transverse oscillation, and found to match very well. The amplitude ratio  $\unicode[STIX]{x1D6FC}$ and phase difference
$\unicode[STIX]{x1D6FC}$ and phase difference 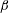 $\unicode[STIX]{x1D6FD}$, in determining the streaming, are also discussed. The number and direction of steady streaming recirculation on the
$\unicode[STIX]{x1D6FD}$, in determining the streaming, are also discussed. The number and direction of steady streaming recirculation on the  $r$–
$r$–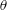 $\unicode[STIX]{x1D703}$ plane depend on value of the amplitude ratio
$\unicode[STIX]{x1D703}$ plane depend on value of the amplitude ratio  $\unicode[STIX]{x1D6FC}$. The phase difference
$\unicode[STIX]{x1D6FC}$. The phase difference 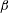 $\unicode[STIX]{x1D6FD}$ plays a dominant role in the azimuthal velocity
$\unicode[STIX]{x1D6FD}$ plays a dominant role in the azimuthal velocity 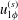 $u_{1\unicode[STIX]{x1D719}}^{(s)}$ of steady streaming. When
$u_{1\unicode[STIX]{x1D719}}^{(s)}$ of steady streaming. When 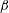 $\unicode[STIX]{x1D6FD}$ is approximately
$\unicode[STIX]{x1D6FD}$ is approximately 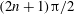 $(2n+1)\unicode[STIX]{x03C0}/2$,
$(2n+1)\unicode[STIX]{x03C0}/2$, 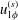 $u_{1\unicode[STIX]{x1D719}}^{(s)}$ vanishes under low-frequency oscillation, while steady streaming has a recirculation on the
$u_{1\unicode[STIX]{x1D719}}^{(s)}$ vanishes under low-frequency oscillation, while steady streaming has a recirculation on the  $r$–
$r$–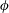 $\unicode[STIX]{x1D719}$ plane under higher-frequency oscillation.
$\unicode[STIX]{x1D719}$ plane under higher-frequency oscillation.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 2
- Cited by



