Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T22:05:59.379Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal mixing in three-dimensional plane Poiseuille flow at high Péclet number

Published online by Cambridge University Press:  10 July 2018

L. Vermach Open the ORCID record for L. Vermach [Opens in a new window]  and
C. P. Caulfield Open the ORCID record for C. P. Caulfield [Opens in a new window]
L. Vermach
Affiliation:
Cambridge Centre for Analysis, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
C. P. Caulfield*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a passive zero-mean scalar field organised into two layers of different concentrations in a three-dimensional plane channel flow subjected to a constant along-stream pressure gradient. We employ a nonlinear direct-adjoint-looping method to identify the optimal initial perturbation of the velocity field with given initial energy which yields ‘maximal’ mixing by a target time horizon, where maximal mixing is defined here as the minimisation of the spatially integrated variance of the concentration field. We verify in three-dimensional flows the conjecture by Foures et al. (J. Fluid Mech., vol. 748, 2014, pp. 241–277) that the initial perturbation which maximises the time-averaged energy gain of the flow leads to relatively weak mixing, and is qualitatively different from the optimal initial ‘mixing’ perturbation which exploits classical Taylor dispersion. We carry out the analysis for two different Reynolds numbers (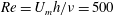$Re=U_{m}h/\unicode[STIX]{x1D708}=500$ and 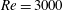$Re=3000$, where 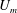$U_{m}$ is the maximum flow speed of the unperturbed flow, 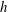$h$ is the channel half-depth and $\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid) demonstrating that this key finding is robust with respect to the transition to turbulence. We also identify the initial perturbations that minimise, at chosen target times, the ‘mix-norm’ of the concentration field, i.e. a Sobolev norm of negative index in the class introduced by Mathew et al. (Physica D, vol. 211, 2005, pp. 23–46). We show that the ‘true’ variance-based mixing strategy can be successfully and practicably approximated by the mix-norm minimisation since we find that the mix-norm-optimal initial perturbations are far less sensitive to changes in the target time horizon than their optimal variance-minimising counterparts.

JFM classification

Flow Control: Flow Control Mixing: Mixing Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 850 , 10 September 2018 , pp. 875 - 923
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aamo, O. M. & Krstić, M. 2003 Flow Control by Feedback: Stabilization and Mixing. Springer.Google Scholar
Aamo, O. M. & Krstić, M. 2004 Feedback control of particle dispersion in bluff body wakes. Intl J. Control 77, 1001–1018.Google Scholar
Aamo, O. M., Krstić, M. & Bewley, T. R. 2003 Control of mixing by boundary feedback in 2D channel flow. Automatica 39, 1597–1606.Google Scholar
Aref, H. 1984 Stirring by chaotic advection. J. Fluid Mech. 143, 1–21.Google Scholar
Balogh, A., Aamo, O. M. & Krstić, M. 2005 Optimal mixing enhancement in 3-D pipe flow. IEEE Trans. Control Syst. Technol. 13, 27–41.Google Scholar
Benson, H. Y., Shanno, D. F. & Vanderbei, R. J. 2003 A comparative study of large-scale nonlinear optimization algorithms. In High Performance Algorithms and Software for Nonlinear Optimization, pp. 95–127. Springer.Google Scholar
Bergman, T. L., Incropera, F. P., DeWitt, D. P. & Lavine, A. S. 2011 Fundamentals of Heat and Mass Transfer. Wiley.Google Scholar
Betz, D.2001 Physical mechanisms of mixing. PhD thesis, University of California, San Diego.Google Scholar
Bewley, T. R. 2008 Numerical Renaissance: Simulation, Optimization, and Control. Renaissance Press.Google Scholar
Brandt, L. 2014 The lift-up effect: the linear mechanism behind transition and turbulence in shear flows. Eur. J. Mech. (B/Fluids) 47, 80–96.Google Scholar
Carlson, D. R., Widnall, S. E. & Peeters, M. F. 1982 A flow-visualization study of transition in plane Poiseuille flow. J. Fluid Mech. 121, 487–505.Google Scholar
Cherubini, S., De Palma, P., Robinet, J.-C. & Bottaro, A. 2010 Rapid path to transition via nonlinear localised optimal perturbations in a boundary layer flow. Phys. Rev. E 82, 066302.Google Scholar
Dennis, J. E. Jr & Schnabel, R. 1996 Numerical Methods for Unconstrained Optimization and Nonlinear Equations. SIAM.Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.Google Scholar
Dimotakis, P. E. & Catrakis, H. J. 1999 Turbulence, fractals, and mixing. In Mixing, pp. 59–143. Springer.Google Scholar
Douglas, S. C., Amari, S. & Kung, S. 1998 Gradient adaptation under unit-norm constraints. In Proceedings of Ninth IEEE SP Workshop on Statistical Signal and Array Processing, pp. 144–147. IEEE.Google Scholar
Duguet, Y., Monokrousos, A., Brandt, L. & Henningson, D. S. 2013 Minimal transition thresholds in plane Couette flow. Phys. Fluids 25, 084103.Google Scholar
Eckart, C. 1948 An analysis of stirring and mixing processes in incompressible fluids. J. Mar. Res. 7, 265–273.Google Scholar
Farazmand, M. 2017 Optimal initial condition of passive tracers for their maximal mixing in finite time. Phys. Rev. Fluids 2, 054601.Google Scholar
Foures, D. P. G., Caulfield, C. P. & Schmid, P. J. 2013 Localization of flow structures using ∞-norm optimization. J. Fluid Mech. 729, 672–701.Google Scholar
Foures, D. P. G., Caulfield, C. P. & Schmid, P. J. 2014 Optimal mixing in two-dimensional plane Poiseuille flow at finite Péclet number. J. Fluid Mech. 748, 241–277.Google Scholar
Hinch, E. J. 1999 Mixing: turbulence and chaos: an introduction. In Mixing, pp. 37–56. Springer.Google Scholar
Juniper, M. P. 2011 Triggering in the horizontal Rijke tube: non-normality, transient growth and bypass transition. J. Fluid Mech. 667, 272–308.Google Scholar
Kerswell, R. R., Pringle, C. C. T. & Willis, A. P. 2014 An optimization approach for analysing nonlinear stability with transition to turbulence in fluids as an exemplar. Rep. Prog. Phys. 77 (8), 085901.Google Scholar
Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Klingmann, B. G. B. 1992 On transition due to three-dimensional disturbances in plane Poiseuille flow. J. Fluid Mech. 240, 167–195.Google Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98 (2), 243–251.Google Scholar
Lemoult, G., Aider, J.-L. & Wesfreid, J. E. 2012 Experimental scaling law for the subcritical transition to turbulence in plane Poiseuille flow. Phys. Rev. E 85 (2), 025303.Google Scholar
Lin, Z., Thiffeault, J.-L. & Doering, C. R. 2011 Optimal stirring strategies for passive scalar mixing. J. Fluid Mech. 675, 465–476.Google Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.Google Scholar
Luo, L. & Schuster, E. 2009 Mixing enhancement in 2D magnetohydrodynamic channel flow by extremum seeking boundary control. In American Control Conference, 2009 (ACC’09), pp. 1530–1535. IEEE.Google Scholar
Mathew, G., Mezi, I. & Petzold, L. 2005 A multiscale measure for mixing. Physica D 211, 23–46.Google Scholar
Mathew, G., Mezić, I., Grivopoulos, S., Vaidya, U. & Petzold, L. 2007 Optimal control of mixing in Stokes fluid flows. J. Fluid Mech. 580, 261–281.Google Scholar
Monokrousos, A., Bottaro, A., Brandt, L., Di Vita, A. & Henningson, D. S. 2011 Nonequilibrium thermodynamics and the optimal path to turbulence in shear flows. Phys. Rev. Lett. 106, 134502.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re = 590. Phys. Fluids 11, 943–945.Google Scholar
Orr, W. M. F. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part I: a perfect liquid, Part II: a viscous liquid. Proc. R. Irish Acad. A 27, 69–138.Google Scholar
Orszag, S. A. 1971 Accurate solution of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50, 689–703.Google Scholar
Ottino, J. M. 1989 The Kinematics of Mixing: Stretching, Chaos, and Transport. Cambridge University Press.Google Scholar
Ottino, J. M. 1990 Mixing, chaotic advection, and turbulence. Annu. Rev. Fluid Mech. 22, 207–254.Google Scholar
Paul, E. L., Atiemo-Obeng, V. A. & Kresta, S. M. 2004 Handbook of Industrial Mixing: Science and Practice. Wiley.Google Scholar
Polak, E. 1971 Computational Methods in Optimization: A Unified Approach, Mathematics in Science and Engineering, vol. 77. Academic Press.Google Scholar
Pringle, C. C. T. & Kerswell, R. R. 2010 Using nonlinear transient growth to construct the minimal seed for shear flow turbulence. Phys. Rev. Lett. 105, 154502.Google Scholar
Pringle, C. C. T., Willis, A. P. & Kerswell, R. R. 2012 Minimal seeds for shear flow turbulence: using nonlinear transient growth to touch the edge of chaos. J. Fluid Mech. 702, 415–443.Google Scholar
Rabin, S. M. E., Caulfield, C. P. & Kerswell, R. R. 2012 Triggering turbulence efficiently in plane Couette flow. J. Fluid Mech. 712, 244–272.Google Scholar
Rhines, P. B. & Young, W. R. 1983 How rapidly is a passive scalar mixed within closed streamlines? J. Fluid Mech. 133, 133–145.Google Scholar
Rothstein, D., Henry, E. & Gollub, J. P. 1999 Persistent patterns in transient chaotic fluid mixing. Nature 401 (6755), 770–772.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows, Applied Mathematical Sciences, vol. 142. Springer.Google Scholar
Sturman, R., Ottino, J. M. & Wiggins, S. 2006 The Mathematical Foundations of Mixing: The Linked Twist Map as a Paradigm in Applications: Micro to Macro, Fluids to Solids. Cambridge University Press.Google Scholar
Taylor, G. I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Taylor, G. I. 1954 The dispersion of matter in turbulent flow through a pipe. Proc. R. Soc. Lond. A 223 (1155), 446–468.Google Scholar
Taylor, J. R.2008 Numerical simulations of the stratified oceanic bottom boundary layer. PhD thesis, University of California, San Diego.Google Scholar
Thiffeault, J.-L. 2012 Using multiscale norms to quantify mixing and transport. Nonlinearity 25 (2), R1–R44.Google Scholar
Thiffeault, J.-L. & Childress, S. 2003 Chaotic mixing in a torus map. Chaos 13, 502–507.Google Scholar
Tsukahara, T., Seki, Y., Kawamura, H. & Tochio, D. 2005 DNS of turbulent channel flow at very low Reynolds numbers. In TSFP Digital Library Online. Begel House.Google Scholar
Vinokur, M. 1983 On one-dimensional stretching functions for finite-difference calculations. J. Comput. Phys. 50, 215–234.Google Scholar
Welander, P. 1955 Studies on the general development of motion in a two-dimensional, ideal fluid. Tellus 7, 141–156.Google Scholar
Wiggins, S. 1992 Chaotic transport in dynamical systems. NASA STI/Recon Technical Report A 92, 28228.Google Scholar
Wiggins, S. & Ottino, J. M. 2004 Foundations of chaotic mixing. Phil. Trans. R. Soc. Lond. A 362, 937–970.Google Scholar