Article contents
Optimal dynamo action by steady flows confined to a cube
Published online by Cambridge University Press: 13 October 2015
Abstract
Many flows of electrically conducting fluids can spontaneously generate magnetic fields through the process of dynamo action, but when does a flow produce a better dynamo than another one or when is it simply the most efficient dynamo? Using a variational approach close to that of Willis (Phys. Rev. Lett., vol. 109, 2012, 251101), we find optimal kinematic dynamos within a huge class of stationary and incompressible flows that are confined in a cube. We demand that the magnetic field satisfies either superconducting (T) or pseudovacuum (N) boundary conditions on opposite pairs of walls of the cube, which results in four different combinations. For each of these set-ups, we find the optimal flow and its corresponding magnetic eigenmodes. Numerically, it is observed that swapping the magnetic boundary from T to N leaves the magnetic energy growth nearly unchanged, and both 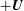 $+\boldsymbol{U}$ and
$+\boldsymbol{U}$ and 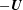 $-\boldsymbol{U}$ are optimal flows for these different but complementary set-ups. This can be related to work by Favier & Proctor (Phys. Rev. E, vol. 88, 2013, 031001). We provide minimal lower bounds for dynamo action and find that no dynamo is possible below an enstrophy (or shear) based magnetic Reynolds number
$-\boldsymbol{U}$ are optimal flows for these different but complementary set-ups. This can be related to work by Favier & Proctor (Phys. Rev. E, vol. 88, 2013, 031001). We provide minimal lower bounds for dynamo action and find that no dynamo is possible below an enstrophy (or shear) based magnetic Reynolds number 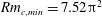 $Rm_{c,min}=7.52{\rm\pi}^{2}$, which is a factor of
$Rm_{c,min}=7.52{\rm\pi}^{2}$, which is a factor of 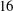 $16$ above the Proctor/Backus bound.
$16$ above the Proctor/Backus bound.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 13
- Cited by



